蒙特卡洛模拟方法

本文来自加州大学洛杉矶分校计算机科学专业的本科生OneRaynyDay，他喜欢用清晰易懂且不失幽默的方式讲述机器学习概念，尤其是其中的数学概念。相比作者这个“数学怪胎”，小编能力有限，只能尽力去计算验证和补齐文中未介绍的概念。如果内容有误，欢迎在留言中指出。

蒙特卡洛是座赌城

目录

简介

蒙特卡洛动作值

初识蒙特卡洛

蒙特卡洛控制

Monte Carlo ES On-Policy：ϵ -Greedy Policies Off-policy：重要性抽样

Python里的On-Policy Model

在强化学习问题中，我们可以用马尔可夫决策过程（MDP）和相关算法找出最优行动值函数 q∗(s,a)和v∗(s)，它通过策略迭代和值迭代找出最佳策略。

这是个好方法，可以解决强化学习中随机动态系统中的许多问题，但它还有很多限制。比如，现实世界中是否真的存在那么多明确知道状态转移概率的问题？我们可以随时随地用MDP吗？

那么，有没有一种方法既能对一些复杂度过高的计算进行近似求解，又能处理动态系统中的所有问题？

这就是我们今天要介绍的内容——蒙特卡洛方法。

简介

蒙特卡洛是摩纳哥大公国的一座知名赌城，里面遍布轮盘赌、掷骰子和老虎机等游戏，类似的，蒙特卡洛方法的建模机制也基于随机数和统计概率。

和一般动态规划算法不同，蒙特卡洛方法（MC）以一个全新的视角来看待问题。简而言之，它关注的是：我需要从环境中进行多少次采样，才能从不良策略中辨别出最优策略？

论智注：关于动态规划算法和MC的视角差异，我们可以举这两个例子：

问：1+1+1+1+1+1+1+1 =？ 答：（掰手指）8。 问：在上式后再+1呢？ 答：9！ 问：怎么这么快？ 答：因为8+1=9。 ——动态规划：记住求过的解来节省时间！

问：我有一个半径为R的圆和一把豆子，怎么计算圆周率？ 答：在圆外套一个边长为2R的正方形，往里面随机扔豆子。 问：此话怎讲？ 答：如果扔了N颗豆，落入圆里的豆子有n颗。N越大，n/N就越接近πR2/4R2。 ——MC：手工算完全比不过祖冲之，我好气！

为了从数学角度解释MC，这里我们先引入强化学习中的“return”（R），也就是“回报”概念，计算agent的长期预期收益（G）：

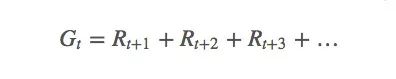
有时候，当前策略的状态概率在这个episode内是非零的，它在之后连续多个episode里也是非零的，我们就要综合考虑当前回报和未来回报的重要程度。

这不难理解，强化学习的回报往往有一定滞后性。比如下围棋时，当前下的子可能目前看来没有多大用处，但它在之后的局势中可能会显示出巨大的优势或劣势，因此我们的围棋agent需要考量长期回报。这个衡量标准就是折扣因子γ：

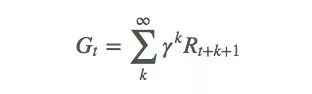
γ一般在[0,1]之间。当γ=0时，只考虑当前回报；当γ=1时，均衡看待当前回报和未来回报。

有了收益Gt和概率At，我们就能计算当前策略下，状态s的函数值V(s)：

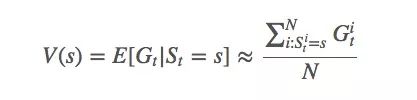
根据大数定律，当N逼近∞时，我们可以得到确切的函数期望值。我们对第i次模拟进行索引。可以发现，如果使用的是MDP（可以解决99%的强化学习问题），由于它有很强的马尔可夫性，即确信系统下个状态只与当前状态有关，与之前的信息无关：

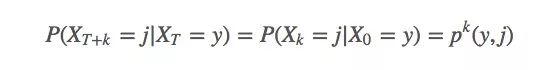
我们可以推导出这样一个事实：t和期望值完全没有关系。所以我们可以直接用Gs来表示从某个状态开始的期望回报（将状态前移到t = 0时）。

初识蒙特卡洛

计算值函数最经典的方法是对状态s的每个first visit进行采样，然后计算平均值，也就是first-visit MC prediction。下面是找到最优V的算法：

pi = init_pi()

returns = defaultdict(list)

for i in range(NUM_ITER):

episode = generate_episode(pi) # (1)

G = np.zeros(|S|)

prev_reward = 0

for (state, reward) in reversed(episode):

reward += GAMMA * prev_reward

# backing up replaces s eventually,

# so we get first-visit reward.

G[s] = reward

prev_reward = reward

for state in STATES:

returns[state].append(state)

V = { state : np.mean(ret) for state, ret in returns.items() }

另一种方法则是every-visit MC prediction，即计算s的所有visit的平均值。虽然两者有轻微不同，但同样的，如果visit次数够大，它们最后会收敛到相似值。

蒙特卡洛动作值

如果我们有一个完整的模型，我们只需知道当前状态值，就能选择一个可以获得最高回报的动作。但如果不知道模型信息呢？蒙特卡洛的特色是无需知道完整的环境知识，只需经验就能学习。因此当我们不知道什么动作会导致什么状态，或者环境内部会存在什么互动性时，我们用的是动作值q*，而不是MDP中的状态值。

这就意味着我们估计的是qπ(s,a)，而不是vπ(s)，回报G[s]也应该是G[s,a]。如果原来G的空间维数是S，现在就成了S×A，这是个很大的空间，但我们还是得继续对其抽样，以找出每个状态动作元组（state−action pair）的预期回报。

正如上一节提到的，蒙特卡洛计算值函数的方法有两种：first-visit MC和every-visit MC。因为搜索空间过大，如果策略过于贪婪，我们就无法遍历每个state−action pair，做不到兼顾exploration和exploitation。关于这个问题的解决方法，我们会在下一节具体讲述。

蒙特卡洛控制

我们先来回顾一下MDP的策略迭代方式：

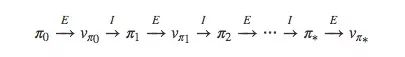
对于蒙特卡洛方法，它的迭代方式并没有我们想象中的不同，也是先从π开始，然后是qπ0，再是π′……

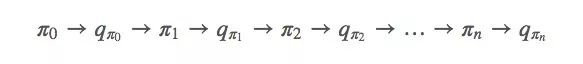
论智注：从π到q的过程代表的是一个完整的策略评估过程，而从q到π则代表一个完整的策略过程。其中策略评估过程会产生很多episode，得到很多接近真实函数的action-value函数。和vπ0一样，虽然这里我们估计出的每个动作值都是一个近似值，但通过用值函数的近似值进行迭代，经过多轮迭代后，我们还是可以收敛到最优策略。

既然qπ0和vπ0并没有那么不同，MDP可以用动态规划法求解，那么我们也可以继续套用贝尔曼最优性方程（Bellman optimality equation），即：

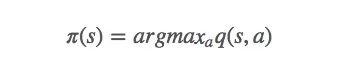
如果不理解，这里有一份中文介绍：增强学习（三）——MDP的动态规划解法。

下面就是exploration vs. exploitation。

Monte Carlo ES

面对这么大一个搜索空间，一个补救方法是假定我们每个episode都会从一个特定的状态开始，并采取特定的行动，也就是exploring start，然后从所有可能回报中抽样。它背后的思想是认定我们能从任意状态开始，并在每个episode之初采取所有动作，同时策略评估过程可以利用无限个episode完成。这在很多情况下是不合常理的，但在环境未知问题中却有奇效。

在实际操作中，我们只需在之前的代码块里添加如下内容：

# Before (Start at some arbitrary s_0, a_0)

episode = generate_episode(pi)

# After (Start at some specific s, a)

episode = generate_episode(pi, s, a) # loop through s, a at every iteration.

On-Policy：ϵ -Greedy策略

那么，如果我们不能假设自己能从任意的状态开始并采取任意的动作呢？不再贪婪，不再存在无限个episode，我们是否还能拟合最优策略？

这就是On-Policy的思想。所谓On-Policy，指的是评估、优化现在正在做决策的那个策略；而off-policy改进的则是和现在正在做决策的那个策略不同的策略。

因为我们要“不再贪婪”，最简单的方法就是用ε-greedy：对于任何时刻t的执行“探索”小概率ε<1，我们会有ε的概率会进行exploration，有1-ε的概率会进行exploitation。相比贪婪策略，ϵ-Greedy随机选择策略（不贪婪）的概率是ε/|A(s)|。

现在的问题是，这是否会收敛到蒙特卡洛方法的最优策略π*？——答案是会，但只是个近似值。

ϵ-Greedy收敛

让我们从q和一个ϵ-greedy策略π′(s)开始：

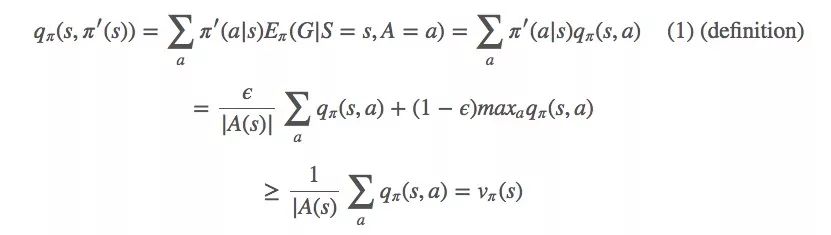
ϵ-greedy策略像贪婪策略一样对vπ做单调改进。如果回到每一步细看，就是：

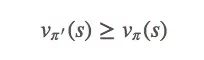
（1）

这是我们的收敛目标。

这只是理论上的结果，它真的能拟合吗？显然不行，因为最优策略是固定的，而我们选择的策略是被迫随机的，所以它不能保证收敛到π*——我们来重构我们的问题：

假设我们不用概率ε在随机选择策略，而是无视规则，真正做到了完全随机选择策略，那么我们就能保证得到至少一个最优策略。即，如果（1）里的等式成立，那么我们就有π=π'，因此vπ=vπ'，受环境约束，这时我们获得的策略是随机情况下最优的。

Off-policy：重要性抽样

Off-policy注释

我们先来看一些定义：

π：目标策略，我们希望能优化这些策略已获得最高回报；

b：动作策略，我们正在用b生成π之后会用到的各种数据；

π(a|s)>0⟹b(a|s)>0∀a∈A：整体概念。

Off-policy策略通常涉及多个agent，其中一个agent一直在生成另一个agent试图优化的数据，我们分别称它们为行为策略和目标策略。就像神经网络比线性模型更“有趣”，同样的，Off-policy策略一般也比On-Policy策略更好玩，也更强大。当然，它也更容易出现高方差，更难收敛。

重要性采样则是统计学中估计某一分布性质时使用的一种方法。它在这里充当的角色是回答“给定Eb[G]，Eπ[G]是什么”？换句话说，就是我们如何使用从b抽样得到的信息来确定π的预期回报？

直观来看，如果b选了很多a，π也选了很多a，那b在π中应该发挥着重要作用；相反地，如果b选了很多a，π并不总是跟着b选a，那b因a产生的状态不会对π因a产生的状态产生过大影响。

以上就是重要性采样的基础思想。给定从t到T的策略迭代轨迹(Si,Ai)Ti=t，策略π拟合这个轨迹的可能性是：

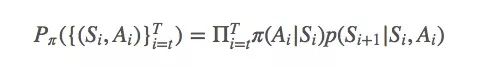
简单地说，π和b之间的比率就是：

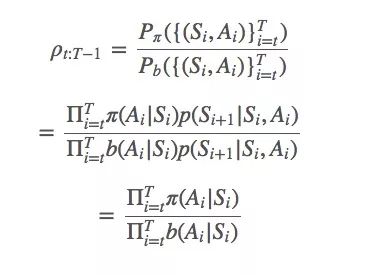
一般重要性采样

现在我们有很多方法可以用ρt:T−1计算Eπ[G]的最优解，比如一般重要性采样（ordinary importance sampling）。设我们采样了N个episode：

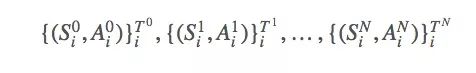
s的首次出现时间是：

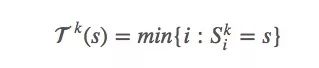
因为要估计vπ(s)，所以我们可以用之前提到的first-visit方法计算均值来估计值函数。

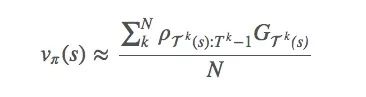
这里用first-visit只是为了简便，我们也可以把它扩展到every-visit。事实上，我们应该结合不同方法来衡量每个episode的回报，因为如果π能拟合最优策略的轨迹，我们应该给它更多权重。

这种重要性抽样方法是一种无偏差估计，它可能存在严重的方差问题。想想那个重要性比率，如果在第k轮的某个episode之中，ρT(s):Tk−1=1000，这就太大了，但它完全有可能存在。那这个1000会造成多大影响？如果我们只有一个episode，它的影响可想而知，但因为强化学习任务往往很长，再加上里面有很多乘法计算，这个比例会存在爆炸和消失两种结果。

加权重要性采样

为了降低方差，一种可行的方法是加入权重来计算总和：

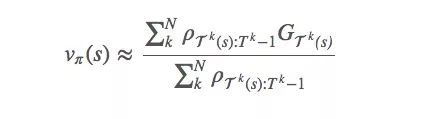
这被称为加权重要性采样（weighted importance sampling）。它是一个有偏差的估计（偏差趋于0），但与此同时方差降低了。如果是实践，强烈建议加权！

增量式实现

蒙特卡洛预测方法也可以采用增量式的实现方式，假设我们使用上节中的加权重要性采样，那么我们可以得到如下形式的一些抽样算法：

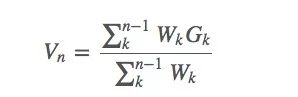
其中Wk是我们的权重。

假设我们有了估计值Vn和当前获得的回报Gn，要利用Vn与Gn来估计 Vn+1，同时，我们用∑nkWk表示前几轮回报的权重之和Cn。那么这个等式就是：

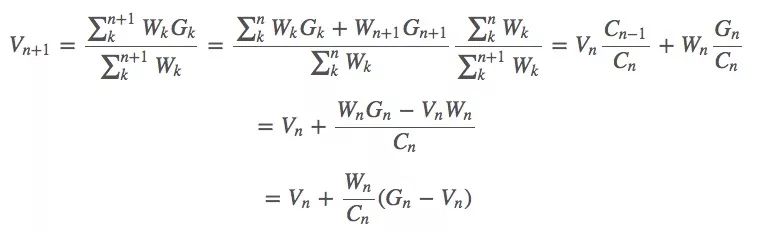
权重：Cn+1=Cn+Wn+1

现在，这个Vn就是我们的值函数，同样的方法也适用于求动作值函数Qn。

在我们更新价函数的同时，我们也可以更新我们的策略π—— argmaxaQπ(s,a)。

注：这里涉及很多数学知识，但已经很基础了，确切地说，最前沿的也和这个非常接近。

下面还有针对折扣因子、奖励的抽样简介，具体请看原文，小编动不了了。

Python里的On-Policy Model

由于蒙特卡洛方法的代码通常具有相似的结构，作者已经在python中创建了一个可以直接使用的蒙特卡洛模型类，感兴趣的读者可以在Github上找到代码。

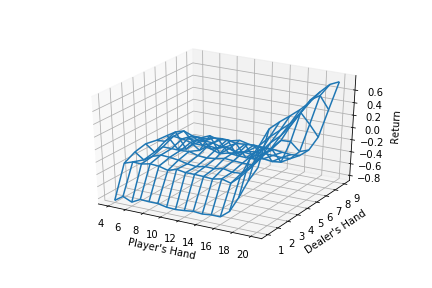
他还在原文中做了示例：用ϵ -greedy policy解决Blackjack问题。

总而言之，蒙特卡洛方法利用episode的采样学习最佳值函数和最佳策略，它无需建立对环境的充分认知，在不符合马尔可夫性时性能稳定，是一种值得尝试的好方法，也是新人接触强化学习的一块良好基石。

本文参考阅读：

[1]增强学习（二）——马尔可夫决策过程MDP：https://www.cnblogs.com/jinxulin/p/3517377.html

[2]增强学习（四）——蒙特卡罗方法(Monte Carlo Methods)：http://www.cnblogs.com/jinxulin/p/3560737.html

[3]算法-动态规划 Dynamic Programming--从菜鸟到老鸟：https://blog.csdn.net/u013309870/article/details/75193592

[4]蒙特卡罗用于计算圆周率pi：http://gohom.win/2015/10/05/mc-forPI/

[5]蒙特卡洛方法 （Monte Carlo Method）：https://blog.csdn.net/coffee_cream/article/details/66972281