纯数字电路的FPGA，实现平方根是比较麻烦的

我知道，我对与电子有关的所有事情都很着迷，但不论从哪个角度看，今天的现场可编程门阵列(FPGA)，都显得“鹤立鸡群”，真是非常棒的器件。如果在这个智能时代，在这个领域，想拥有一技之长的你还没有关注FPGA，那么世界将抛弃你，时代将抛弃你。

作为纯数字电路的FPGA，实现平方根是比较麻烦的。毕竟硬件不支持这种算法。

好在厂家的IP核中有相关的平方根IP库，所以用起来也很方便。

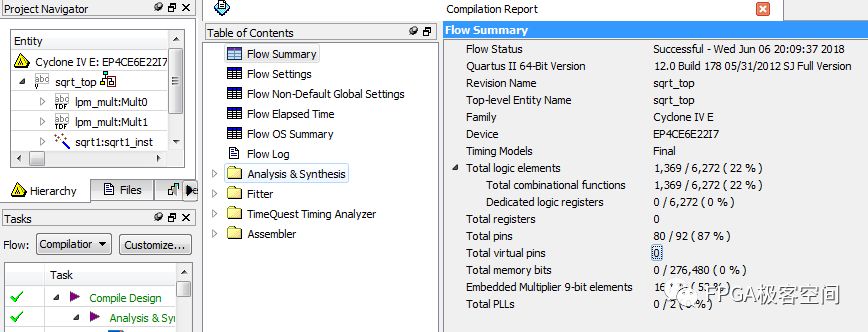
上图是在QUARTUS下调用库中的IP核，综合适配后的资源使用情况，逻辑单元使用的1369个，占总资源的22%，片上硬件乘法器使用了16个。可以说是在资源有限的情况下，使用资源量还是很大的。

前几篇文章中，我们介绍了使用CORDIC算法计算三角函数sin和cos的值。计算三角函数sin和cos的值是利用CORDIC算法的旋转模式来进行的。而在向量模式下，可以使用CORDIC算法计算平方根。

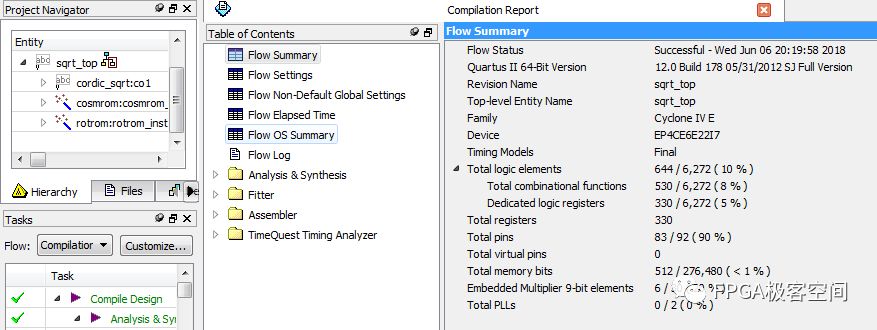
如图，使用CORDIC算法计算平方根，FPGA资源的使用情况。逻辑单元使用了10%，乘法器使用的6个，片上ram只是用的不到1%。可以说在资源有限的情况下，是非常好的选择 。但是要注意，算法本身可使用流水线操作，也可使用其他方式操作，计算周期要根据迭代的次数决定，迭代次数越大，计算越精确，同样，计算的周期也越长。

上图是迭代16次后的结果，可以清楚地看到，输入xi，yi，输出sqrt_out，结果非常精确。在时序不是很紧的情况下，可以使用这种方法。

具体详细的算法，可根据之前介绍的CORDIC算法自行推理。