RLC网络直接可以利用相量分析方法给出稳态解

最近看到一网友的一个问题，就是个不能再简单的RLC网络。那个帖子中的一个仿真见下图：

通常，RLC网络直接可以利用相量分析方法给出稳态解，如下图：

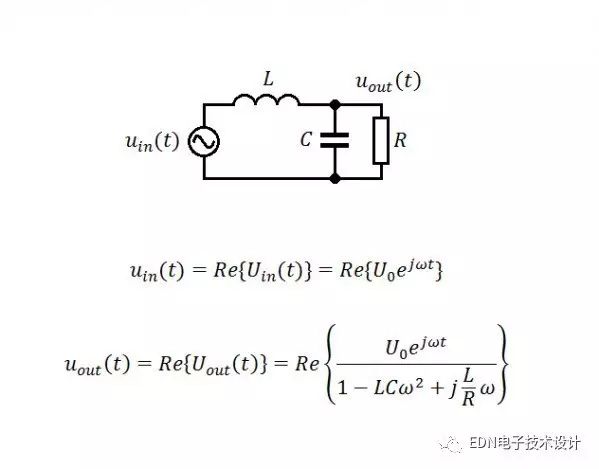
显然，上面的那个相量方法所得的结果与首帖中的那个仿真相距甚远。问题出在那里？

其实，相量分析的前提是单频稳态，那就限制了许多的自由度。下面将考虑其它因素，采用拉普拉斯变换进行分析，见下图：

拉普拉斯分析的最大特点就是考虑了系统的初始状态，譬如图中的V0（电容的初始电压）和I0（电感的初始电流）。注意上图中的两个式子，上式给出了那个含初始状态的RLC网络的解，而下式则是采用了分部分式分解。对照相应的系数，可得下面的方程组：

由那个RLC网络输出响应式子，可直接看出所谓的“零状态响应”和“零输入响应”，见下式：

这些式子太简单，不是本帖的主题。下面先看看那个仿真图的情形，见下图：

这是个零状态响应，输入为一个余弦电压信号：Uin = U0 cos(ωt)注意，其响应是两个等幅度但不同频率的余弦信号的叠加，那就是首帖的仿真结果——差拍。

可能有人会问，拉普拉斯分析方法能否过渡到相量分析方法上去？当然可以，否则就不合理了。拉普拉斯分析中只要选择适当的初始条件，就能使系统自身的“自然特性”不显现出来，具体见下图：

最后，需要特别指出的是，下式：

给出了其响应可以分解为系统自身特征和外部激励特征这两部分之和。显见，如果存在电阻R（R≠∞），那么系统自身的自然特征部分将随着时间推移呈指数衰减。最终趋近于相量分析法！