补充: FPGA产生基于LFSR的伪随机数

       大家好，又到了每日学习的时间了，上一篇《荐读：基于FPGA 的CRC校验码生成器》文中，提到了“要实现这一过程，仍然需要LFSR电路，参看《FPGA产生基于LFSR的伪随机数》中关于该电路特性的介绍”，在这补一篇《FPGA产生基于LFSR的伪随机数》，欢迎大家交流学习。
       
       1.概念
       通过一定的算法对事先选定的随机种子(seed)做一定的运算可以得到一组人工生成的周期序列，在这组序列中以相同的概率选取其中一个数字，该数字称作伪随机数，由于所选数字并不具有完全的随机性，但是从实用的角度而言，其随机程度已足够了。这里的“伪”的含义是，由于该随机数是按照一定算法模拟产生的，其结果是确定的，是可见的，因此并不是真正的随机数。伪随机数的选择是从随机种子开始的，所以为了保证每次得到的伪随机数都足够地“随机”，随机种子的选择就显得非常重要，如果随机种子一样，那么同一个随机数发生器产生的随机数也会一样。

       2.由LFSR引出的产生方法
       产生伪随机数的方法最常见的是利用一种线性反馈移位寄存器(LFSR),它是由n个D触发器和若干个异或门组成的，如下图：
       


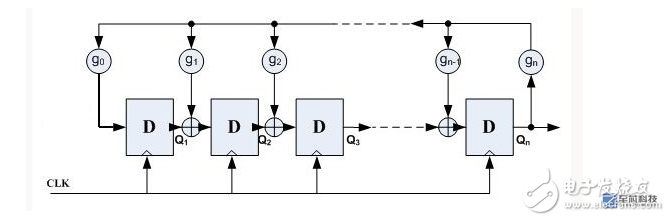
       其中，gn为反馈系数，取值只能为0或1，取为0时表明不存在该反馈之路，取为1时表明存在该反馈之路；n个D触发器最多可以提供2^n-1个状态(不包括全0的状态)，为了保证这些状态没有重复，gn的选择必须满足一定的条件。下面以n=3，g0=1，g1=1,g2=0,g3=1为例，说明LFSR的特性，具有该参数的LFSR结构如下图：
       

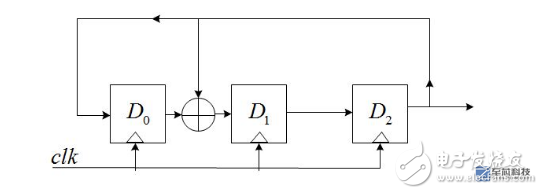
       假设在开始时，D2D1D0=111(seed)，那么，当时钟到来时，有：

       D2=D1_OUT=1；

       D1=D0_OUT^D2_OUT=0；

       D0=D2_OUT=1；

       即D2D1D0=101；同理，又一个时钟到来时，可得D2D1D0=001. ………………

       画出状态转移图如下：
       


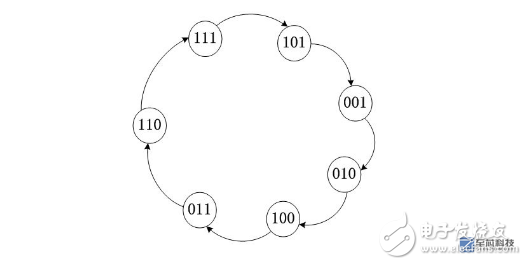
       从图可以看出，正好有2^3-1=7个状态，不包括全0；

       如果你理解了上图，至少可以得到三条结论：

       1)初始状态是由SEED提供的；

       2)当反馈系数不同时，得到的状态转移图也不同；必须保证gn===1,否则哪来的反馈？

       3)D触发器的个数越多，产生的状态就越多，也就越“随机”；


       3.verilog实现

       基于以上原理，下面用verilog产生一个n=8，反馈系数为g0g1g2g3g4g5g6g7g8=101110001的伪随机数发生器，它共有2^8=255个状态，该LFSR的结构如下：
       

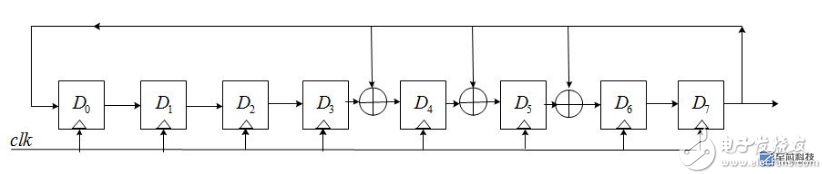
       verilog源代码如下：
       


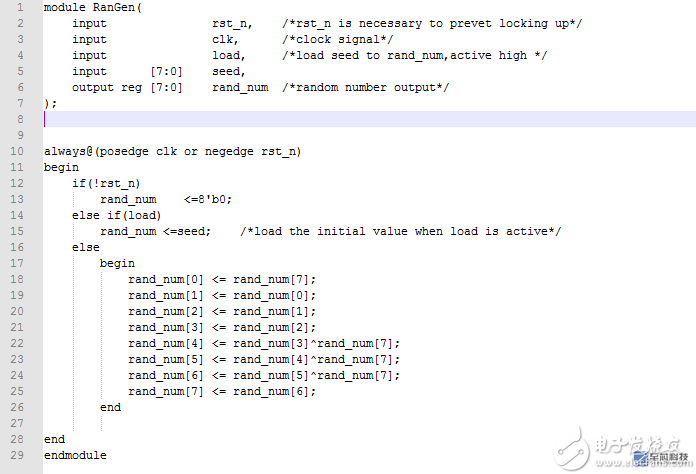
       仿真波形：
       
       
       以1111 1111为种子，load信号置位后，开始在255个状态中循环，可将输出值255、143、111……作为伪随机数。

       这篇补充就说到这里，各位，加油。