SVD的简介和主要应用领域以及原理与几何意义

1 简介

SVD 全称：Singular Value Decomposition。SVD 是一种提取信息的强大工具，它提供了一种非常便捷的矩阵分解方式，能够发现数据中十分有意思的潜在模式。

主要应用领域包括：

隐性语义分析 (Latent Semantic Analysis, LSA) 或隐性语义索引 (Latent Semantic Indexing, LSI)；

推荐系统 (Recommender system)，可以说是最有价值的应用点；

矩阵形式数据（主要是图像数据）的压缩。

2 线性变换

在做 SVD 推导之前，先了解一下线性变换，以 2*2 的线性变换矩阵为例，先看简单的对角矩阵：

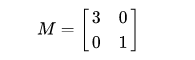
从集合上讲， M 是将二维平面上的点（x，y）  经过线性变换到另一个点的变换矩阵，如下所示：

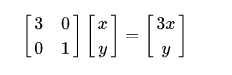
该变换的几何效果是，变换后的平面沿着x水平方向进行了3倍拉伸，垂直方向没有发生变化。

3 SVD 推导

该部分的推导从几何层面上去理解二维的SVD，总体的思想是：借助 SVD 可以将一个相互垂直的网格 (orthogonal grid) 变换到另外一个互相垂直的网格。

可以通过二维空间中的向量来描述这件事情。

首先，选择两个互相正交的单位向量v1和v2（也可称为一组正交基）。

M 是一个变换矩阵。

向量Mv1 , Mv2 也是一组正交向量（也就是v1和v2 经过M变换得到的）。

u1， u2分别是Mv1, Mv2的单位向量（即另一组正交基），且有：

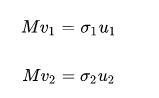
则，σ1，σ2 分别为 Mv1 , Mv2的模（也称为M的奇异值）。

设任意向量x，有：

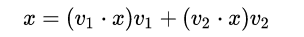
根据线代知识，向量的内积可用向量的转置来表示：

至此，SVD 使用几何意义的形式推导完毕，其中：

关于 SVD 的一些重要的结论性总结：

任意的矩阵M是可以分解成三个矩阵；

V表示了原始域的标准正交基；

U表示经过M变换后的新标准正交基；

∑表示了V中的向量与U中相对应向量之间的比例（伸缩）关系；

∑中的每个σ会按从大到小排好顺序，值越大代表该维度重要性越高；

在利用 SVD 做数据信息提取或压缩时，往往依据一些启发式策略，如直接设定只提取∑  中的前 k项，或者另一种较常用的做法是保留矩阵中一定百分比的能量信息，一般可设定为 90%，能量信息比例的计算可先求得所有奇异值平方总和，然后将奇异值的平方依次累加到总值的 90% 为止，形如： 

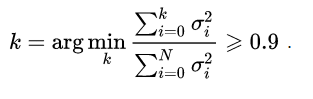
# -*- coding: utf-8 -*-

import numpy as np

import numpy.linalg as la

import matplotlib.pyplot as plt

from sklearn import datasets

from skimage import io

def getImgAsMat(index):

ds = datasets.fetch_olivetti_faces()

return np.mat(ds.images[index])

def getImgAsMatFromFile(filename):

img = io.imread(filename, as_grey=True)

return np.mat(img)

def plotImg(imgMat):

plt.imshow(imgMat, cmap=plt.cm.gray)

plt.show()

def recoverBySVD(imgMat, k):

# singular value decomposition

U, s, V = la.svd(imgMat)

# choose top k important singular values (or eigens)

Uk = U[:, 0:k]

Sk = np.diag(s[0:k])

Vk = V[0:k, :]

# recover the image

imgMat_new = Uk * Sk * Vk

return imgMat_new

# -------------------- main --------------------- #

#A = getImgAsMat(0)

#plotImg(A)

#A_new = recoverBySVD(A, 20)

#plotImg(A_new)

A = getImgAsMatFromFile('D:/pic.jpg')

plotImg(A)

A_new = recoverBySVD(A, 30)

plotImg(A_new)