

数字示波器提供的工具如何用来表征噪声
描述
每个电路都有一定的噪声,这些噪声会影响模拟和数字电路的性能。有些噪声来自外部干扰,有些噪声则由热效应等随机因素引起。随机产生的噪声要比已知来源的噪声更难以表征,因为没有哪次测量提供了关于上一次或下一次测量的任何信息。这种过程只能通过对许多事件的多次测量、并用下次某个具体事件的概率来描述。许多数字示波器提供的工具可以用来表征噪声。一旦了解了噪声的特征,就有办法减轻噪声。
要用数字示波器分析诸如电气噪声等随机信号,就需要能够提供随机过程多个视图的工具。图1是多维示波器工具的预览图。
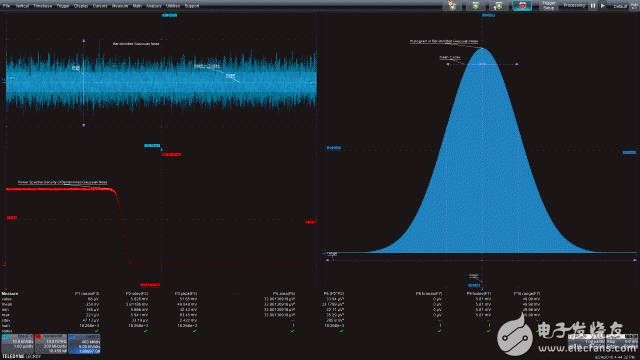 图1:左上图是带宽受限的高斯噪声的时域图,左下图是功率谱密度,是带宽受限噪声的频域图;右面的柱状图是带宽受限噪声的统计图。这三个视图都因采用了有助于对测量进行量化的测量参数而得到增强。
图1:左上图是带宽受限的高斯噪声的时域图,左下图是功率谱密度,是带宽受限噪声的频域图;右面的柱状图是带宽受限噪声的统计图。这三个视图都因采用了有助于对测量进行量化的测量参数而得到增强。
显示在图1左上部分的曲线是带宽受限的高斯噪声的时域图。我们在整篇文章中引用的都是这个信号。下面的曲线显示的是频域中的噪声:信号的功率谱密度(PSD)显示了每赫兹的噪声功率与频率的关系。右图是带宽受限噪声的柱状图,通过近似随机过程的概率密度函数(PDF)提供统计视图。这些曲线的下方显示了一系列的测量参数,用于量化通过数学计算得到的波形。下面我们将详细了解每种测量技术,看看每种方法能够呈现带宽受限噪声信号哪些内容。
1、噪声或抖动
噪声和抖动是相互关联的。噪声是叠加到有用信号上的不想要的垂直信号分量;抖动是信号时序发生了不想要的变化。噪声信号被施加到诸如逻辑门这样的阈值比较器上时就变成了抖动。由垂直噪声引起的幅度变化会使输出早于或晚于阈值交越的理想时序。用于测量噪声的工具和过程同样可用于测量抖动。
对于接到示波器输入通道的信号可以直接进行噪声测量,抖动测量则是基于时序测量,比如时间间隔误差(TIE)、周期或占空比。对输入信号开展的这些时序测量都是一个周期一个周期进行的。使用称为轨迹或时间轨迹的数学函数,可以将测量结果按时间绘制出来。这种轨迹函数就是随后用于抖动测量的输入信号。
2、时域
测量参数可以应用于图2中的噪声波形,以深入了解这种噪声信号的特性。图中显示的参数有平均值、标准偏差和峰峰值。显示器下方显示了读取的参数值。
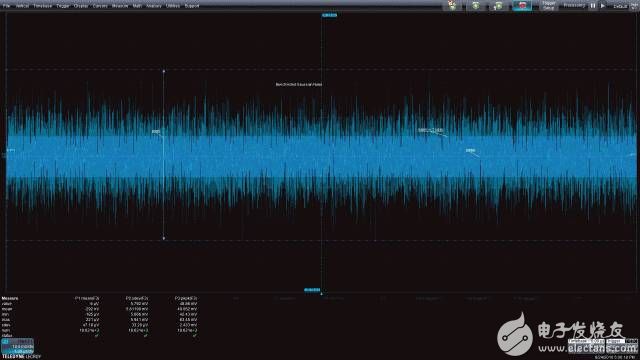 图2:带宽受限噪声信号的时域图。参数值显示了基本测量、平均值、标准偏差或交流均方根、峰峰值。
图2:带宽受限噪声信号的时域图。参数值显示了基本测量、平均值、标准偏差或交流均方根、峰峰值。
参数标记在随机波形上,图形化显示了测量结果。标准偏差也可以被称为交流耦合的均方根(rms)值,因为它描述了波形的有效幅度,因此也许是最有用的。平均值是指信号的平均值,采集过程中出现的最大和最小幅度之差则用峰峰值表示。除了读取指定采集过程的所选参数,示波器还可以计算和显示多次采集后每种参数的累积统计结果,提供每种参数的均值、最大值、最小值和标准偏差。
2.1、柱状图:统计域视图
随机过程最好是在统计域中用柱状图进行描述。图3显示了上述带宽受限的噪声信号的柱状图及源波形。这张柱状图将满刻度电压范围分为5000份,并计算落在每一范围内的采样值数量。垂直轴是每一范围内的样本数量,正比于该值发生的概率,水平轴是幅度值,本例中是电压值。
带宽受限噪声信号的柱状图是经典的贝尔曲线,具有高斯或正常概率密度函数的特征。如果知道波形的方差(标准偏差的平方)和均值,就可以完整地描述概率密度函数。另外要注意,这种分布围绕均值呈对称特性。
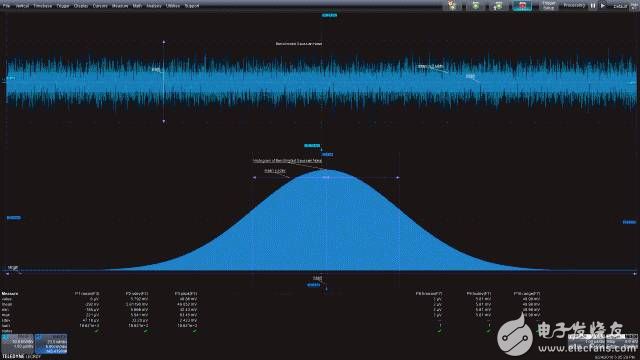 图3:带宽受限噪声信号的柱状图呈现出典型的高斯贝尔形状的响应。柱状图参数读取柱状图均值、标准偏差和范围。
图3:带宽受限噪声信号的柱状图呈现出典型的高斯贝尔形状的响应。柱状图参数读取柱状图均值、标准偏差和范围。
测量参数也可以应用于柱状图。在这个例子中是柱状图均值(hmean)、标准偏差(hstdev)和范围(hrange)。注意,这些读数与前面测量时间波形得到的均值、标准偏差和峰峰值非常接近,两者之间很小的差别是对柱状图样本的“分割”造成的。
高斯分布围绕均值呈对称特性,随着幅度远离均值,幅度值的概率会下降。虽然极端幅度(称为尾巴)发生的概率很低,但仍然是可能发生的。极端幅度不会到零意味着高斯分布是没有边界的。只要有足够多的样本,很大幅度的样本也是有可能出现的。图4显示了一些典型的概率密度函数。高斯分布是最上面那个图形。
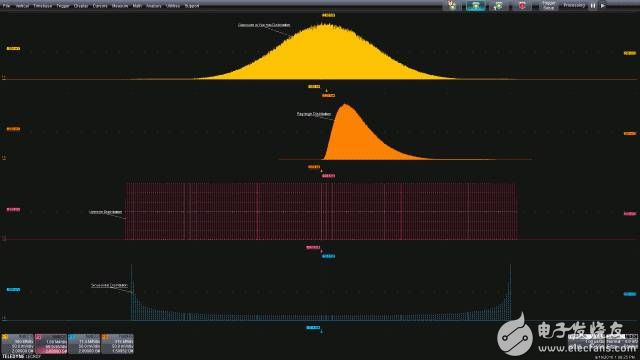 图4:包括高斯、瑞利、均匀和正弦在内的一组概率密度函数。
图4:包括高斯、瑞利、均匀和正弦在内的一组概率密度函数。
从上往下数第二张图是瑞利分布。这是一种不对称的分布,是将高斯分布噪声施加到峰值检测器造成的。这种分布表明概率密度函数不需要是对称的。
从上至下数第三张图是一种均匀分布。这种分布出现在时序测量中,比如触发事件和示波器采样第一个样本之间的时间。在均匀分布中,所有样值都具有相同的概率。这种分布是有边界的。
最底下那张图显示的是同样具有边界约束的正弦分布。这种分布呈马鞍形状,最大概率发生在幅度极值点(最大和最小值点)。
在许多应用中,两个或多个随机过程可能发生交互。当这种情况发生时,过程的概率密度会进行数学卷积运算。一个常见的例子是结合了随机和确定性抖动分量的时序抖动。图5显示了结合在一起的高斯和正弦分量,源分布位于上面两张图,从上往下数的第三张分布图是两个源卷积的结果。许多先进的示波器提供可选的抖动或噪声分析包,这些分析包可以将这些组合式分布分开,单独测量分量。
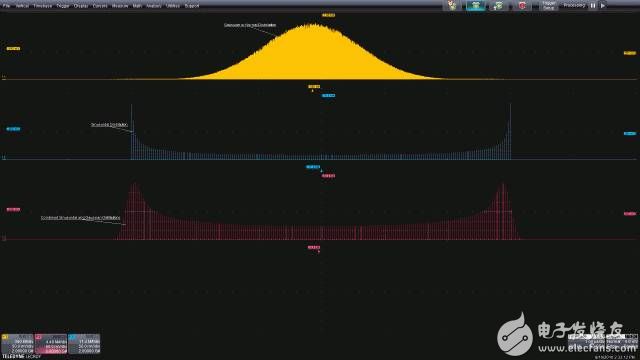 图5:当高斯和正弦分布组合在一起时形成的概率密度函数是两个源概率密度函数的卷积。
图5:当高斯和正弦分布组合在一起时形成的概率密度函数是两个源概率密度函数的卷积。
3、频域分析
单位频率上的功率(即功率谱密度PSD)是最常见的频域噪声分析工具。图6给出了一个例子,上部是带宽受限高斯噪声的时域图,下部是带宽受限噪声的功率谱密度。
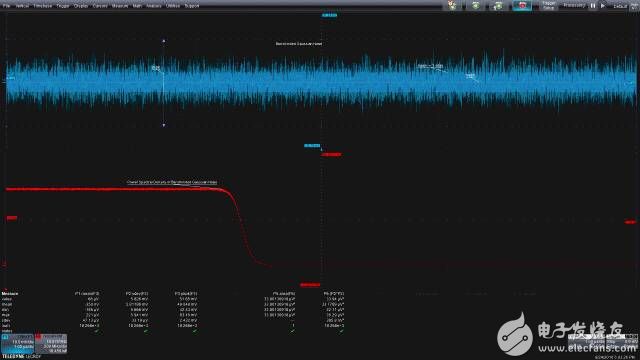
本例中功率谱密度的测量单位是V2/Hz。这条曲线是用示波器的快速傅里叶变换(FFT)计算出来的,选用的是输出类型幅度平方而不是默认的分贝(dBm)刻度。除了输出类型,我们还选择了矩形加权和最小素因数FFT。这种FFT可以报告分辨率带宽Δf,在本例中是100kHz,以及加权函数的有效噪声带宽(ENBW),针对矩形加权的值为1.000。
为了计算功率谱密度,平均后的FFT输出必须被归一化为有效FFT带宽。此外,这个示波器的FFT输出经校准可读取峰值而不是均方根值。为了转换回均方根值,FFT幅度值必须乘上0.707,幅度平方值必须乘上0.5。必须使用Rescale数学函数将FFT值除以FFT的有效带宽才能将该值归一化为单位带宽(1Hz)。Rescale函数可以通过一个乘数因子并加减偏移量重新调整数值。在我们这个例子中,乘数是0.5/100E3 = 5E-6。乘数因子0.5在前面已经讨论过。另外一个因子是有效FFT带宽的倒数,是分辨率带宽乘以等效噪声带宽(ENBW)。如果选择了矩形以外的加权函数,ENBW将是大于1的值。Rescale函数还能改变单位,在本例中单位被设为V2/Hz。你可能已经注意到,再构造数学函数也已经用于将浮点FFT输出的映射优化进参数测量中使用的整数数学空间。
参数P2测量时域波形的标准偏差参数。P6使用参数数学公式实现标准偏差的平方,得到噪声信号的方差。参数P5代表功率谱密度曲线下方的面积,这个面积也是噪声信号的方差,只不过是从功率谱密度计算出来的。两种方法计算出来的方差值基本上是相等的,相差不到0.1%。
在频域中分析随机过程可以帮助你细分不同频率产生的噪声。本例中的面积测量可以覆盖整个FFT范围。你也可以使用测量选通门将测量限制在指定频带内,以判断特定频谱区域的噪声情况。在带宽等于FFT有效噪声带宽的情况下,示波器的光标可以读取特定频率处的功率谱密度。
4、派生参数
峰值因数,即波形峰值与均方根值之比,可以帮助你确定处理信号峰值变化所需的动态范围。虽然我们使用的示波器没有双极性“峰值”参数,但我们借助通道1中信号的绝对值可以很容易地创建一个。这样可以将负值“翻转”进波形的正值区域,进而让你使用最大值参数读取每次采集数据的最大正峰或负峰值。注意,这种方法是因为信号有零均值才起作用的。然后我们就可以使用参数数学公式计算峰值与均方根值之比的峰值因数。图7显示了这种测量。
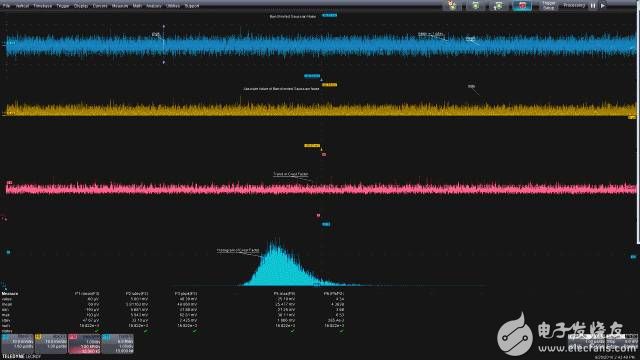 图7:测量峰值与均方根值之比的信号峰值因数。所测信号的绝对值使得所有峰值呈单极性,因此最大值参数返回的就是每次采集数据的最大峰值。参数数学公式可计算出最大值与标准偏差(均方根)值之比值,即峰值因数。
图7:测量峰值与均方根值之比的信号峰值因数。所测信号的绝对值使得所有峰值呈单极性,因此最大值参数返回的就是每次采集数据的最大峰值。参数数学公式可计算出最大值与标准偏差(均方根)值之比值,即峰值因数。
最上边的波形是带宽受限的噪声信号。参数P2是噪声波形的标准偏差(交流耦合的均方根值)。下面一个波形显示了噪声波形的绝对值,这个波形是单极性的。源波形中的最高正负峰值已成为最高绝对峰值。使用最大值参数得到这个参数。
参数P5是绝对波形曲线的最大值。参数P6使用参数数学公式计算每次采集数据的峰值因数,即P5(max)与P2(rms)的比值。P6参数统计显示了当前值、均值、最小最大标准偏差以及峰值因数测量值总数。在本例所示超过15000次采集中,峰值因数从3.68变到6.53,平均值为4.38。
从上往下第三张图是峰值因数的趋势曲线,按测量顺序显示了每一次测量的峰值因数。趋势图下方是峰值因数的柱状图。从图中可以看出,峰值因数测量结果大多在均值附近,仅在均值的最右边有少量的高值测量结果。
5、总结
你可以使用现代数字示波器中的时域、频域和统计域工具量化诸如噪声和抖动等随机过程,并通过相关的测量参数进行增强。包括均值、标准偏差和范围在内的统计参数可以帮助你了解被测的过程。参数数学公式可以推导出派生参数,比如方差和峰值因数。
-
如何用示波器测量确定性抖动2009-09-23 1309
-
示波器的噪声来源及电源纹波噪声的测试方法2017-11-14 1235
-
示波器如何处理有噪声的信号2019-11-11 0
-
如何用数字示波器测量信号的周期和振幅?2023-05-06 0
-
用示波器工具简化测量处理有噪声的信号2008-11-26 563
-
使用示波器测试和表征当前的电源2016-12-19 562
-
如何用示波器修开关电源2017-11-06 2276
-
示波器是测量电源纹波和电源噪声的必备工具2018-03-12 19889
-
数字示波器的抖动噪声基底是什么2019-08-30 4534
-
示波器的噪声来源 如何用示波器减小波形噪声2020-03-15 10133
-
如何用示波器去测量脉冲信号呢2021-10-04 16241
-
一文从三方面分析噪声的来源2023-06-25 1391
-
如何用示波器测量一个信号的频率?2023-09-12 10242
-
模拟示波器和数字示波器的区别2024-05-11 2937
-
如何使用示波器测量有噪声的信号2024-05-17 2503
全部0条评论

快来发表一下你的评论吧 !

