一些能够解决生活中一些具体问题的常用算法的整理集合

这是一篇八千字的长文，是一些算法笔记的整理集合，希望能给你帮助。

曾经有一个著名的骗局：

小明是一个赌马爱好者，最近他连续几次提前收到了预测赌马结果的邮件，从一开始由于不屑而错失良机，到渐渐深信不疑，直到最后给邮件发送方汇了巨款才发现上当。

看过这个的人应该知道，骗子收集到一份邮件信息后，分组发送不同预测结果的邮件，赌马结果公布后，再将筛选出来的那部分人分组，继续发送下一轮预测邮件。几轮过后，肯定能保证一部分人收到的预测结果是完全正确的。这也是最关键的部分。

那么骗子是如何从几万或几十万用户中寻找这些“幸运儿”的呢？这是一种二分法的思想。

假如要顺序在100万人中寻找一个人，最多需要100万次，而二分法只需要18次。

下面讲讲一些能够解决生活中一些具体问题的常用算法。

二分查找

对于一个长度为N的数组，简单查找最多需要N步；二分查找最多只需要logN步（约定底数为2）。

二分查找相较于简单查找，极大地提高了效率，但是二分查找的前提是列表是有序的，这也导致了诸多限制。

下面使用二分法编写一个查找算法。

Python实现

1def binary_search(list,target): 2    #查找的起点和终点 3    low=0 4    high=len(list)-1 5    # 6    while (low<=high): 7        #若low+high为奇数，则向下取整 8        mid=(low+high)//2 9        temp=list[mid]10        if target==temp:11            return mid12        elif temp>target:13            high=mid-114        else:15            low=mid+116    return None17if __name__ == '__main__':18    test_list=[1,2,4,5,12,32,43]19    print(binary_search(test_list,4))20    print(binary_search(test_list, 44))

输出结果:

122None

递归

想象这么一个问题，在一个大盒子里，有若干个小盒子，在这些小盒子里也可能有更小的盒子。在所有盒子中，其中一个盒子内有一把钥匙，如何找到这把钥匙?

有两种思路：

第一种：

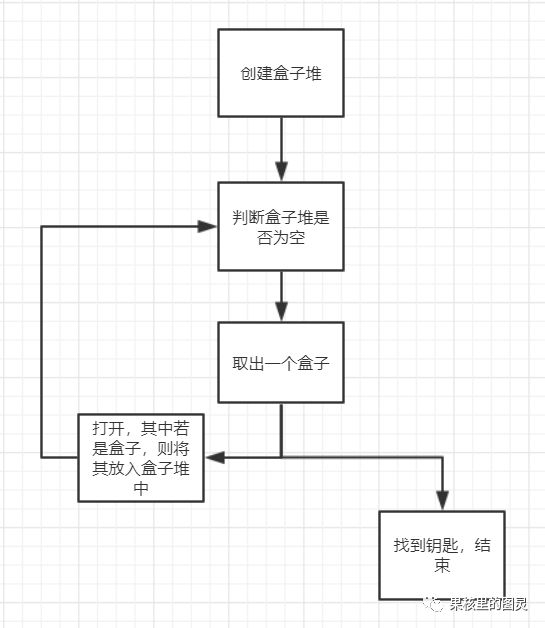
image.png

第二种

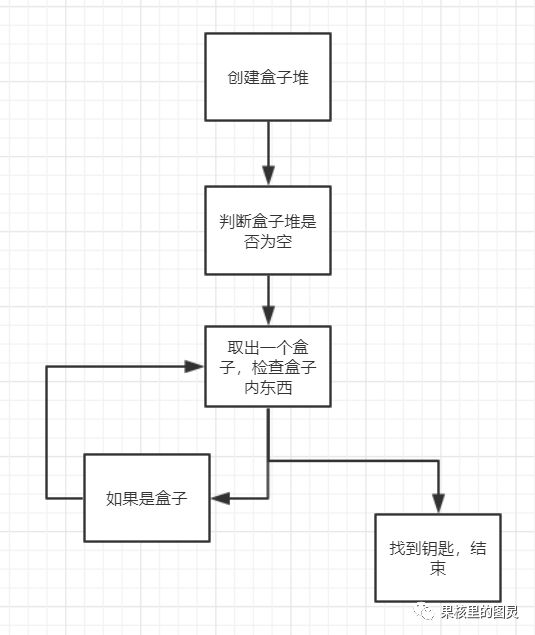
image.png

哪一种思路更加清晰呢？我们用代码来实现一下：

第一种首先新建两个类型盒子和钥匙：

1class Box: 2    name=None 3    box=None 4    key=None 5    def __init__(self,name): 6        self.name=name 7    def set_box(self,box): 8        self.box=box 9    def set_key(self,key):10        self.key=key11class Key:12    name=None13    def __init__(self,name):14        self.name=name

查找算法：

1def look_for_key(box): 2    pile_box=box 3    i=0 4    while pile_box is not None: 5        #默认取出盒子堆中的第一个 6        handle_box=pile_box[0] 7        print("取出了："+handle_box.name) 8        if handle_box.key is not None: 9            print("在"+handle_box.name+"中找到了钥匙")10            return handle_box.key.name11        elif handle_box.box is not None:12            pile_box.append(handle_box.box)13            print("将"+handle_box.box.name+"放入盒子堆")14        pile_box.remove(handle_box)15    return "没有找到钥匙"

测试数据：

1if __name__ == '__main__': 2    #现在我创建一把钥匙 3    key1=Key("我是钥匙") 4    #现在我将钥匙放在盒子1中 5    b1 = Box("1号盒子") 6    b1.set_key(key1) 7    # 创建多个盒子，互相放置 8    b2=Box("2号盒子") 9    b2.set_box(b1)10    b3=Box("3号盒子")11    b3.set_box(b2)12    b4=Box("4号盒子")13    b4.set_box(b3)14    b5=Box("5号盒子")15    #将这些盒子放入一个大盒子16    main_box=[b4,b5]17    print(look_for_key(main_box))

输出：

1取出了：4号盒子 2将3号盒子放入盒子堆 3取出了：5号盒子 4取出了：3号盒子 5将2号盒子放入盒子堆 6取出了：2号盒子 7将1号盒子放入盒子堆 8取出了：1号盒子 9在1号盒子中找到了钥匙10我是钥匙

第二种（递归方式）

新建类型还是使用之前的，主要是重新写一种查找算法：

1def look_for_key(box): 2    print("打开了"+box.name) 3    if box.key is not None: 4        print("在" + box.name + "中找到了钥匙") 5        return 6    else: 7        look_for_key(box.box) 8if __name__ == '__main__': 9    #现在我创建一把钥匙10    key1=Key("我是钥匙")11    #现在我将钥匙放在盒子1中12    b1 = Box("1号盒子")13    b1.set_key(key1)14    # 创建多个盒子，互相放置15    b2=Box("2号盒子")16    b2.set_box(b1)17    b3=Box("3号盒子")18    b3.set_box(b2)19    b4=Box("4号盒子")20    b4.set_box(b3)21    #将这些盒子放入一个大盒子22    main_box=Box("主盒子")23    main_box.set_box(b4)24    look_for_key(main_box)

输出：

1打开了主盒子2打开了4号盒子3打开了3号盒子4打开了2号盒子5打开了1号盒子6在1号盒子中找到了钥匙

总结以上两种查找方式：使用循环可能使效率更高，使用递归使得代码更易读懂，如何选择看哪一点对你更重要。

使用递归要注意基线条件和递归条件，否则很容易不小心陷入死循环。

 

快速排序

D&C

D&C(divide and conquer)分而治之是一种重要的解决问题思路。当面对问题束手无策时，我们应该考虑一下：分而治之可以解决吗？

现在有一个问题，假如一块土地（1680*640）需要均匀地分为正方形，而且正方形的边长要尽量的大。该怎么分？

这个问题本质就是求两条边长的最大公因数。可以使用欧几里得算法（辗转相除）

1def func(num1,num2): 2    temp=0 3    while(num1%num2): 4        temp=num1%num2 5        num1=num2 6        num2=temp 7    return temp 8if __name__ == '__main__': 9    num1=168010    num2=64011    print(func(num1,num2))

快速排序

快速排序是一种常用的排序算法，比选择排序快得多（O(n^2)）,快速排序也使用了D&C。

选择基准值

将数组分成两个子数组：基准值左边的数组和基准值右边的数组

对这两个数组进行快速排序

来写一下代码实现：

1def quicksort(list): 2    if len(list)<2: 3        return list 4    else: 5        #暂且取第一个值作为基准值 6        pivot=list[0] 7        less=[] 8        greater=[] 9        for item in list:10            if itempivot:13                greater.append(item)14        return quicksort(less)+[pivot]+quicksort(greater)15if __name__ == '__main__':16    test_list=[2,43,53,12,542,3253]17    print(quicksort(test_list))

输出结果：

1[2, 12, 43, 53, 542, 3253]

快速排序的最糟情况是O(n^2),O(n^2)已经很慢了，为什么还要叫它快速排序呢?

快速排序的平均运行时间为O（nlogn）,而合并排序的时间总是O（nlogn），合并排序似乎更有优势，那为什么不用合并排序呢？

因为大O表示法中的n是一个常量，当两种算法的时间复杂度不一样时，即使n在数值上不同，对总时间的影响很小，所以通常不考虑。

但有些时候，常量的影响很大，对快速排序和合并排序就是这样，快速排序的常量小得多，所以当这两种算法的时间复杂度都为O（nlogn）时，快速排序要快得多。而相较于最糟的情况，快速排序遇上平均情况的可能性更大，所以可以稍稍忽视这个问题。（快速排序最糟的情况下调用栈为O(n),在最佳情况下，调用栈长O(logn)）

散列表

使用散列函数和数组可以构建散列表，散列表是包含额外逻辑的数据结构。

但是要编写出完美的散列函数几乎不可能，假如给两个键分配的空间相同的话就会出现冲突。如何处理冲突呢?最简单的办法是：假如在某一空间上产生冲突，就在这一空间后再加上一个链表。但是假如这个链表很长，会很影响查找的速度（链表只能顺序查找，查找时间为O(n)）

所以一个能尽量避免冲突的散列函数是多么重要，那么怎么编写一个性能较高的散列表呢？

较低的填装因子（一旦填装因子大于0.7，就需要调整长度）

良好的散列函数（让数组中的值呈均匀分布，可以了解下SHA函数）

广度优先搜索

广度优先搜索能够解决两个问题：

两个节点之间是否存在相连的路径

最短的距离是多少？这个“最短距离”的含义有很多种。

想象这么一个问题：你想在你的微信好友和好友的好友中寻找是否有人是一名消防员，该如何查找？并且尽可能这人和你的关系更近些。

实现：

1from collections import  deque 2def is_fireman(person): 3    #假设一个很简单的判断，假设消防员的名字尾部为f 4    return person[-1]=='f' 5def search_fireman(search_graph): 6    search_queue=deque() 7    search_queue+=search_graph["i"] 8    while search_queue: 9        person=search_queue.popleft()10        if is_fireman(person):11            return person12        else:13            if search_graph.__contains__(person):14            #假如这个人不是消防员，就将这个人的朋友全加入队列15                search_queue+=search_graph[person]16    return "你的圈子里没有消防员"17if __name__ == '__main__':18    test_graph={}19    test_graph["i"]=["Alice","Abby","Barry"]20    test_graph["Alice"]=["Bob","Tom"]21    test_graph["Abby"]=["Cart","Jay"]22    test_graph["Barry"]=["Welf","Zos"]23    print(search_fireman(test_graph))

输出结果:

1Welf

迪克斯特拉算法

在图中，搜索最小的“段”数可以用广度优先算法，这就相当于默认每条边的权重是相同的，如果每条边的权重不同呢？那就需要用到迪克斯特拉算法。

概括来说，迪克斯特拉算法就是从起点开始，首先寻找最廉价的节点，更新其开销并标记为已处理，然然后在未处理的节点中寻找开销最小的节点，然后以此往复下去。

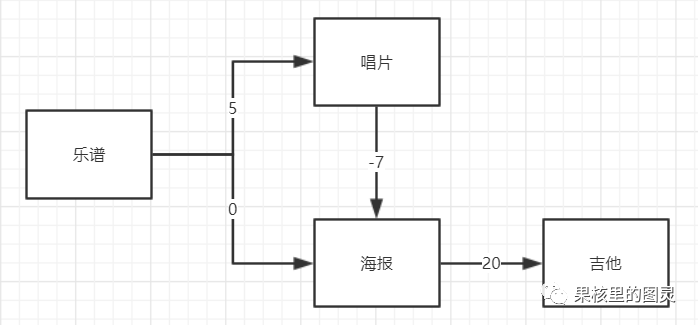
针对书中的这样一个问题，我把题干提取出来：目标是用乐谱换钢琴。现在乐谱可以免费换海报；海报加30元换吉他；海报加35元换架子鼓；乐谱加5元可以换唱片；唱片加15元换吉他；唱片加20元换架子鼓；吉他加20元换钢琴；架子鼓加10元换钢琴。

现在我用图把这个关系表示出来：

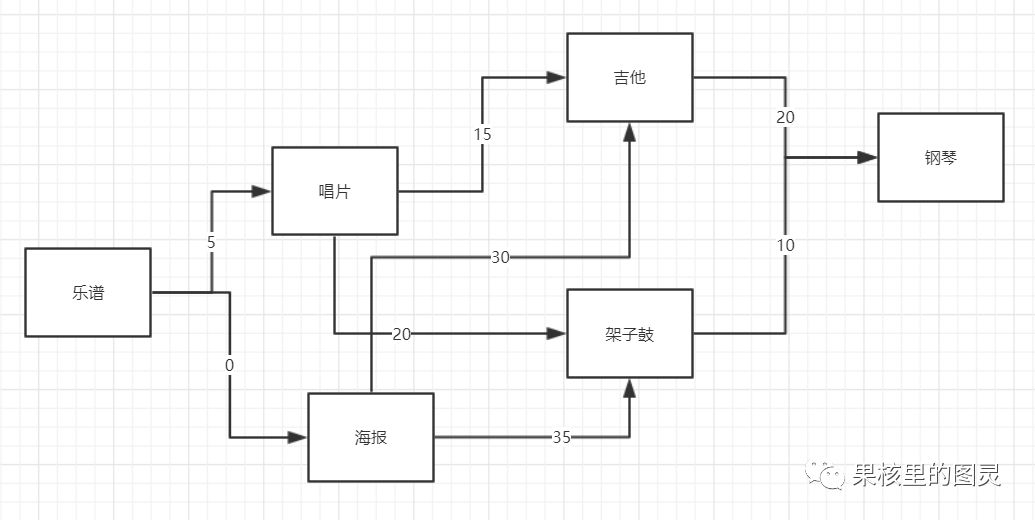
可以看出这是一个加权图，现在我们要使用迪克斯特拉算法寻找最短路径。

代码实现：

1#检索图 2def dijkstra_find(costs,parent,processed): 3    #找到当前最廉价的节点 4    node =lowest_cost_node(costs,processed) 5    while node is not None: 6        cost=costs[node] 7        if not graph.__contains__(node): 8            break 9        neighbours=graph[node]10        for key in neighbours.keys():11            new_cost=cost+neighbours[key]12            if costs.__contains__(key):13                if costs[key] > new_cost:14                    costs[key] = new_cost15                    parent[key] = node16            else:17                costs[key]=new_cost18                parent[key] = node19        processed.append(node)20        node = lowest_cost_node(costs,processed)21#在开销表中寻找最廉价的节点22def lowest_cost_node(costs,processed):23    lowest_cost=float("inf")24    lowest_node=None25    for node in costs:26        cost=costs[node]27        if cost

输出：

最后的最低开销表为：

节点	开销
海报	0
唱片	5
吉他	20
鼓	25
钢琴	35

 

父子节点表为：

父节点	子节点
乐谱	唱片
乐谱	海报
唱片	吉他
唱片	鼓
鼓	钢琴

 

可以看出，最优的交换的路径为：piano-drum-record-music

最低开销为：35元

贝尔曼-福德算法

在迪克特拉斯算法的基础上，我们考虑这样一种情况，假如边的权重存在负值。

在迪克特拉斯算法中，我们首先寻找最廉价的节点，更新其开销，再寻找未处理节点中最廉价的节点，以此往复。

可能出现这样一个情况：

在将海报标记为已处理后，开始处理唱片，但是唱片到海报的路径使得海报的开销更小，又将更新海报的开销，但是海报已经标记为已处理。那么就会出现一些问题。假如继续使用迪克特拉斯算法，最后的结果肯定是错的，大家可以更改参数试一下。为了正确解决问题，这时需要使用贝尔曼-福德算法。

贪心算法

对于一些比较复杂的问题，使用一些算法不能简单有效地解决，这时候往往会使用贪心算法：每步操作都选择局部最优解，最终得到的往往就是全局最优解。这似乎是想当然的做法，但是很多情况下真的行之有效。当然，贪心算法不适用于所有场景，但是他简单高效。因为很多情况并不需要追求完美，只要能找到大致解决问题的办法就行了。

假如我们面对这么一个问题：假设我开了一家网店，在全国各省都有生意，现在面临发快递的问题，假设现在的基础物流不是很完善，每家快运公司只能覆盖很少几个省，那么我该如何在覆盖全国34个省级行政区的情况下，选择最少的快运公司？

这个问题看似不难，其实很复杂。

现在假设有n家快运公司，那么全部的组合有2^n种可能。

N	2^N
10	1024
20	1048576
50	1125899906842624

 

可以看到，假如有50家快递公司，我将要考虑1125千亿种可能。可以看到，没有算法能很快的计算出这个问题，那么我们可以使用贪心算法，求局部最优解，然后将最终得到的视为全局最优解。

那么在这个问题下如何使用贪心算法？核心在于什么是局部最优条件？可以这样：

选择一家覆盖了最多未覆盖省的公司。

重复第一步。

我们在进行测试的时候稍稍简化一下问题，将34个省改为10个省。代码实现：

1def func(company,province): 2    result = set() 3    province_need=province 4    #当存在未覆盖的省时，循环一直继续 5    while province_need: 6        best_company=None 7        province_coverd=set() 8        #查找局部最好的选择 9        for temp_company,temp_province in company.items():10            coverd=province_need & temp_province11            if len(coverd)>len(province_coverd):12                best_company=temp_company13                province_coverd=coverd14        province_need-=province_coverd15        result.add(best_company)16    return result17if __name__ == '__main__':18    province=set(["河北","山西","辽宁","吉林","黑龙江","江苏","浙江","安徽","福建","江西"])19    company={}20    company["顺丰"]=set(["河北","山西","辽宁","江苏","浙江"])21    company["圆通"]=set(["吉林","浙江"])22    company["中通"]=set(["黑龙江","江西"])23    company["韵达"]=set(["江苏","浙江","江苏"])24    company["EMS"]=set(["浙江","安徽","河北","山西"])25    company["德邦"]=set(["福建","江西","安徽"])26    select_company=func(company,province)27    print(select_company)

输出结果：

需要选择这几家快递公司。