关于基于快速模型预测控制的超级电容城轨充电

0 引言

随着城市建设的不断推进，城轨，地铁等便捷、无拥堵的交通工具正在公共交通系统中扮演着越来越重要的角色[1]。超级电容储能式城轨作为一种新兴的城市轨道交通设备，利用了超级电容功率密度大，充放电速度快，寿命长的优点[2]，不再需要大范围架设的牵引电缆，而仅由车载超级电容组供电即可保证列车的正常运行。列车进站时，站台充电机利用乘客上下车的30 s时间为车载超级电容组充电，以维持列车至下一站前的正常运行[3]。

实际运行测算中，需要至少维持430 A的电流使车载超级电容组在30 s内从500 V充满电至900 V。保证充电电流从0 A平稳快速地上升至430 A，同时避免充电过程中出现的电流尖峰破坏功率器件，是设计储能式城轨充电机所需解决的关键问题之一。

考虑到上述的充电要求，储能式城轨超级电容充电可归结为一个带约束的优化问题并采用模型预测控制(MPC)算法进行求解[4]。考虑到基于开关器件的充电电路控制周期很短，将MPC应用于储能式城轨超级电容充电需要解决优化目标快速实时求解的问题，而这也是MPC在电力电子领域应用的一大研究热点[5]。

近年来，众多学者提出了一类简化或改进后的经典优化算法以降低MPC计算复杂度。文献[6]通过对二次规划问题的标准求解算法进行改进提高MPC在线求解的速度；文献[7]引入固定障碍参数的机制，将传统内点法求解由两层迭代简化为一层迭代，使MPC实时计算量大幅降低；文献[8]将传统的牛顿-拉夫逊算法进行扩展，使二次规划问题的求解得到了大幅简化。

本文首先基于MPC算法设计超级电容充电控制率，在最优解求解时，采用改进的内点法实现快速求解。相较于传统方法使障碍参数不断逼近于0，仅用一个经过试验验证的固定参数进行求解；同时采用一种暖启动机制，将该时刻求解值用作下一时刻的初始解，大大简化求解的计算量。通过Matlab仿真对障碍参数进行选取，并利用缩比试验平台验证快速充电策略的有效性。

1 系统建模

1.1 超级电容充电机模型

超级电容充电机基于Buck电路搭建，其系统模型如图1所示。其中采用经典的三分支模型[9]对超级电容进行建模。依据实际需求，此处仅考虑在瞬态过程中占据主导作用的瞬态支路Ri Ci。

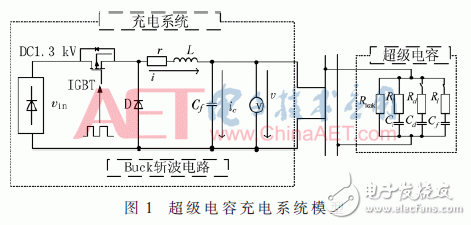
1.2 充电系统模型

基于状态空间平均法的系统模型为：

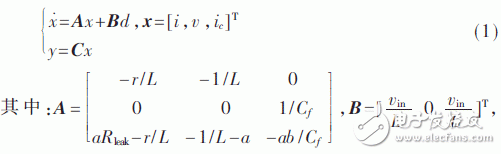
C=[1，0，0]，b=Ri Ci+RleakCi+RleakCf，a=1/CiRiRleak。系统状态量中i为电感电流，v为超级电容端电压，ic为滤波电容电压。r为回路等效阻抗，L为电感，Cf为滤波电容，Ri和Ci分别为超级电容瞬态支路电阻和电容，Rleak为超级电容漏电阻。

进一步取IGBT开关周期Ts为采样周期，进而得到如式(2)所示的充电系统离散时域线性模型：

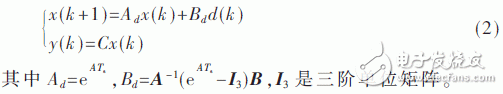
2 充电策略设计

考虑到实际中超级电容充电系统的开关周期达到了1 kHz，本文中综合考虑跟踪精度及计算时间，选取预测时域P和控制时域M均为2。在此基础上，可以得到如式(3)所示的目标函数，其中第一项为对期望电流的跟踪，第二项为对占空比变化量的限制：

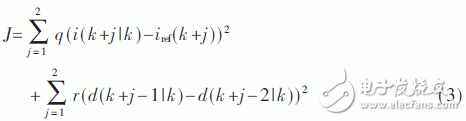
在构建最大峰值电流约束之前，首先给出第k个周期内峰值电感电流的估计式：

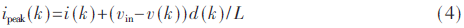
其中(vin-v(k))d(k)/L代表了第k个周期内电感电流所增长的量。在该估计式的基础上，可以得到如下的第k时刻及第(k+1)时刻的电感峰值电流约束关系式：

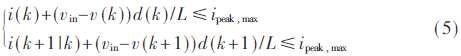
最终所构建的模型预测控制问题转化为一个准二次型规划问题。最终的MPC优化目标如式(6)所示：

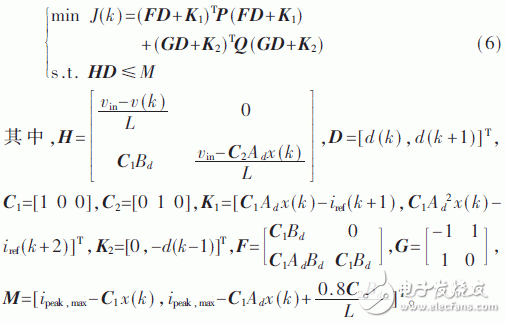
3 目标函数求解

3.1 固定障碍参数法求解

首先引入对数形式的障碍函数将上一节中所构建的MPC优化问题不等式约束转化为等式约束：

其中λ>0被称为障碍参数。当λ趋向于0时，式(8)的解收敛于原MPC优化问题的解。

不同于经典内点法，本文仅选用一个固定障碍参数λ带入优化问题中进行求解，而不再使其逐渐收敛于0。尽管该种机制会导致求解值偏离最优解，但在Steven等人的经典的论文中证实[7]，只要λ选取得当，控制器的性能并不会因为是近似最优解而受到明显的削弱，而求解所需的时间却可以大大的缩短。本文首先设定一个可以反映不同λ下实际控制性能的指标e(k)：

其中ε是常数，e(k)反映了不同时刻下输出电流对参考值的跟踪误差。进而依据e(k)历史曲线选取障碍参数λ。

带入固定障碍参数λ后，可以得到所构建MPC最优问题的最优控制序列D所需满足的条件：

3.2 固定障碍参数选取

Matlab中搭建电路及控制器，设置仿真参数如下：vin=1 300(V)，L=10(mH)，r=0.01(Ω)，Cf=7 200(μF)，Rleak=9(kΩ)，Ri=0.02(Ω)，Ci=24.5(Ω)，Ts=0.001(Ω)。

λ=1，λ=0.1，λ=0.001，λ=0.01时的e(k)历史曲线如图2所示。可以看出λ=0.001时，电流初始上升阶段额e(k)峰值达到约5×10-5，当电流趋于稳定后，在小范围内规律的波动。分析可知，由于求解的控制量为近似最优解，其会在最优控制量附近小范围波动，最终导致了输出电流在期望值附近小范围波动。经对比最终选取λ=0.001作为固定障碍参数。

3.3 暖启动机制

采用固定障碍参数机制后，每次求解所需迭代次数从约50次缩减为仅约10次。为进一步减少求解所需的迭代次数，本文引入另外一种称为热启动的机制。该机制将(k-1)时刻所求解作为k时刻迭代初始解。该方法利用固定障碍参数法将MPC优化问题转化为纯牛顿迭代求解的特性，可进一步使每次迭代求解所需次数缩减为仅仅约5次。相关性能在后续试验中得到进一步验证。

4 仿真

按3.2节设置仿真参数，固定障碍参数λ=0.001，并引入暖启动机制求解，各仿真曲线如图3～图5所示。

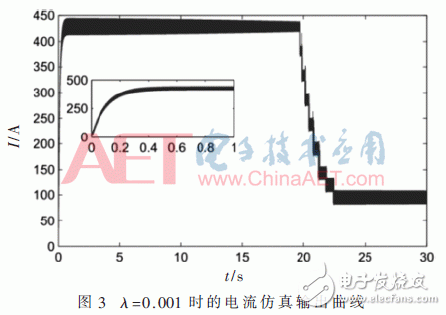
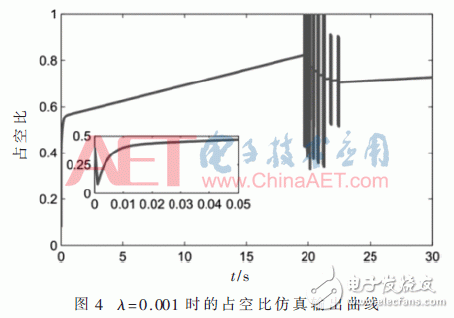
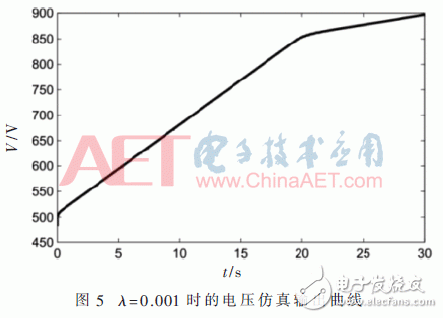
图3可看出电流在前0.3 s内从0 A稳定上升至430 A，随后开始保持稳定。当超级电容电压上升至850 V，充电时间约为20 s时，电流开始缓慢下降，在约2.5 s内最终下降至100 A，直至充电结束。整个过程保持了快速而平稳的趋势，未出现电流尖峰。

图4可看出控制量初始值较大，跌落后开始随超级电容端电压的升高稳步增加。电流从430 A降至100 A的过程中，由于期望电流曲线呈阶梯快速下降的趋势，占空比在0.4至1的范围内有一段抖动，但总体趋势逐渐趋于平缓。满足了优化目标函数中对控制量的约束。

图5可看出从0 s开始，充电电容端电压从500 V开始稳定上升，当升至850 V时，由于充电电流逐渐减小至100 A，超级电容端电压上升速度减缓，最终在充电结束时达到900 V。

5 试验验证

将实际充电系统进行了缩放，在实验室完成进一步试验验证。已有的超级电容模组由18个2.7 V/3 500 F单体的单体串联而成，超级电容负载由2个超级电容模组构成，其等效参数为97.2 V/97.2 F。最终选定以30 A电流对超级电容负载进行充电，其电压变化范围定为30 V～39 V。确定系统功率等级后，设计如图6所示的验证平台，实物图如图7所示。

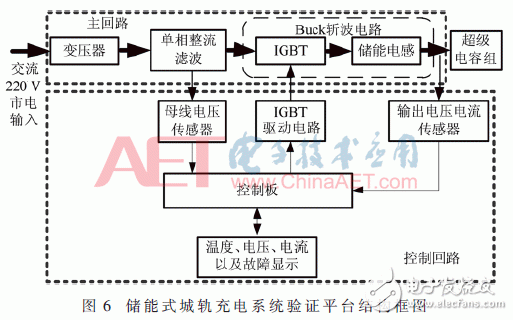
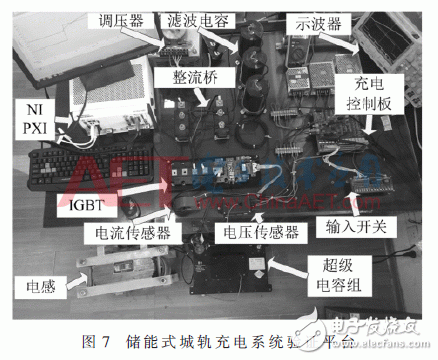
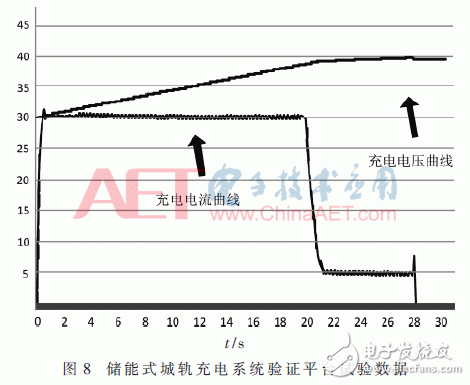
图8为基于验证平台的充电试验数据。从实验数据可看出，充电电流在0.5 s内上升至设定的30 A，尽管出现较小超调，但满足电流快速平稳上升的需求。当超级电容电压升至37 V，充电电流逐渐由30 A减为10 A，最终在超级电容电压达到39 V时停止。整个充电过程充电电流按照期望曲线变化，且满足了峰值电流约束，超级电容在设定时间内由30 V充电至39 V。

6 结论

考虑到快速充电的需求及超级电容模型的复杂性，储能式超级电容城轨列车的充电问题可以归结为一个带约束的最优问题进行求解。MPC在解决有限时域约束问题上有着天然的优势，然而在短时间内求解目标函数是MPC应用至电力电子领域的一大难点。本文提出的改进内点法相较于传统内点法，将求解目标函数所需的迭代步数从50步减小至约仅10步，结合后续提出的暖年启动机制，使求解所需迭代步数缩减至仅约5步，在高效率完成求解的同时，保证了良好的控制效果。仿真及试验可以看出，尽管选用固定障碍参数会带来求解的一定偏差或波动，但整体效果是大大符合预期的。关于进一步优化该算法，提高控制精度的研究，将会在后续的工作中继续展开。