

用迁移学习探明CV任务的底层结构
电子说
描述
今天凌晨,第31届计算机视觉和模式识别大会(CVPR)在美国盐湖城正式召开。本届大会一共收到3309篇投稿文章,最终接受979篇,接受率为29.6%,其中斯坦福和伯克利研究人员合作的Taskonomy: Disentangling Task Transfer Learning斩获最佳论文,图宾根大学教授Andreas Geiger和FAIR何凯明获得PAMI年轻学者奖。
虽然这几天学界大牛都忙着在twitter上谴责特朗普政府的“零容忍”移民政策,但CVPR 2018火热依旧,大会刚开幕,官网就因访问量过大挂了(现已恢复)。下面是论智带来的最佳论文预览,如有错误,欢迎留言指出。
视觉任务之间是否存在相关性?就像表面法线可以被用来简化图像深度估计。针对这些问题,直觉给出了积极的答案,暗示视觉任务中可能存在某种“结构”。掌握这种结构是意义重大的;它是迁移学习的基础,也为确定各种任务之间的冗余提供了理论依据,例如,它允许我们在各种相关任务中无缝重复使用监督,或是用一个模型完成多种任务而不增加复杂度。
本文提出了一种完全计算的方法,从26个2D、2.5D、3D和语义任务中提取迁移学习相关性关系,进而建模视觉任务空间结构。该产品已经上线,是迁移学习的计算分类图。此外,文章还探究了这个结构的作用,比如利用提取到的non-trivial关系减少任务对标记数据量的需求。实验表明,对于10个不同的视觉任务,这种方法可以减少2/3的标记数据量,同时模型的性能和单独训练的模型基本一致。
物体识别、深度估计、边缘检测、姿态估计等都是常见的计算机视觉任务,它们也被学界看作是有价值的研究课题。其中的一些任务是高度相关的,比如我们知道表面法线和深度估计存在衍生关系,空间中消失的点对目标定位也有一定作用。但对于其他关系,我们掌握的知识就很有限了,例如,我们还没有弄清关键点检测和空间中的阴影为什么能被一起用来进行姿态估计。
计算机视觉确实没有明确使用这些关系,近年来学界在开发先进学习模型上已经取得了令人瞩目的成就,如ConvNets,它们能从多对(x, y)中找到X到Y的复杂映射。当然,x∈X,y∈Y,这些前提是训练数据给出的,也就是我们常说的完全监督学习。监督学习的一个缺点是会导致模型只能解决一类孤立的问题,这也意味着每接受一个新任务,模型就得从头开始训练——我们需要大量标记数据。
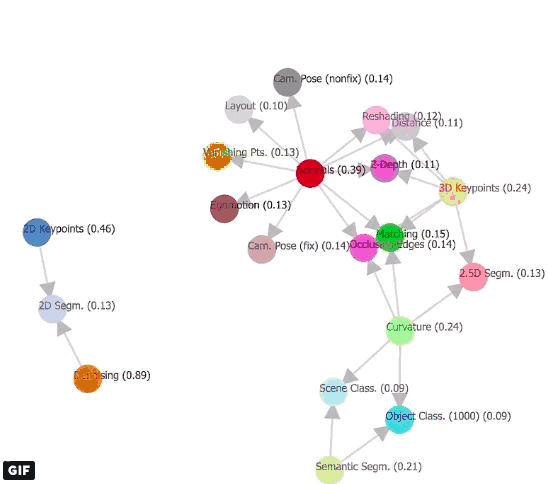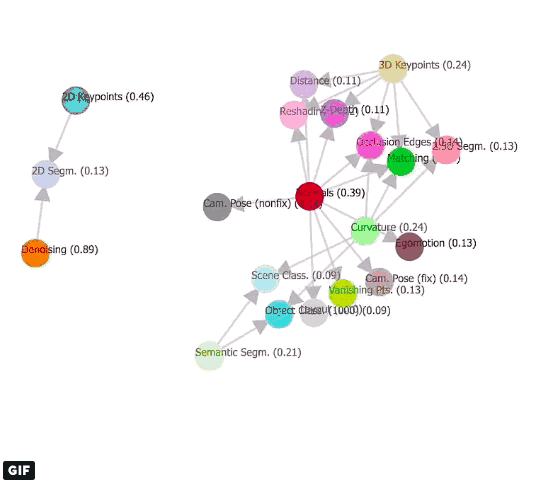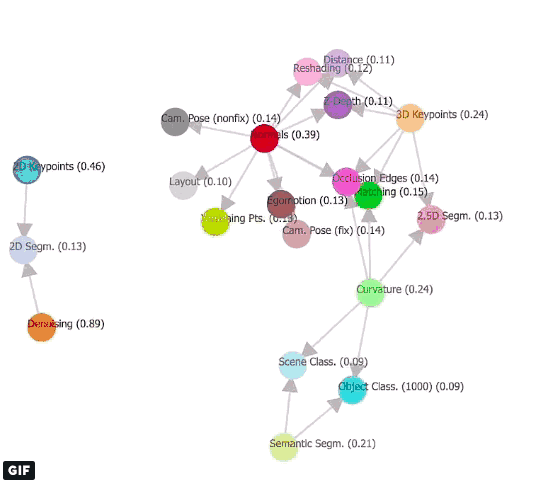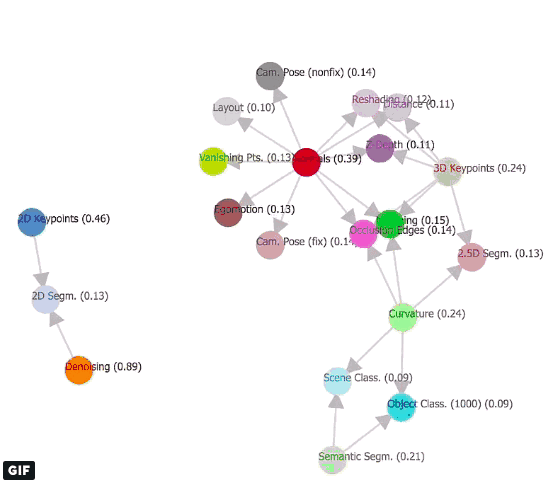
如果模型掌握了各种任务之间的关系,它需要的监督学习就更少,计算压力也更轻,而且预测效率更高。但到目前为止,这个关系是未知的。因此本文的目标是揭示任务空间底层结构,并提出一个计算机视觉任务之间的映射框架。这里的“结构”指的是任务间的相关性集合,即这个任务能给那个任务提供多少有用的信息。
论文作者在这里用的是完全计算的方法,在前馈神经网络中,每一层都包含将输入映射到输出所需信息的抽象表征,这些表征可以被用来计算对输出的贡献程度,继而推导任务之间的相关性矩阵。简而言之,这里需要用到完全抽样的迁移学习,从不同任务中提取相关的迁移策略。经实验证实,最后获得的模型大大降低了对标记数据量的需求,同时这个架构在普通数据集上也能使用。
工具
上述任务可以被定义如下:在有限的监督预算γ内(计算量、数据量和时间限制),我们要在一组任务T = {t1, ..., tn}中实现任务集体性能的最大化。其中γ表示允许从头开始训练的最大任务数(源任务),T表示我们想要完成的任务集(目标任务),S表示可以训练的任务集(源任务),那么
V=T ∪ S是任务词典;
T − T ∩ S是我们想要完成但没法训练的任务(target-only);
T ∩ S既是目标任务,也是源任务;
S − T ∩ S是可以训练的任务,但我们对它们不感兴趣(source-only)。
什么是Taxonomy?
Taxonomy,也就是任务分类法是一个定向的超图模型,它可以从给定任务词典里找出可迁移的元素。正如上文提到的,我们手里有一个源任务集和一个目标任务集,它们相交的边表示一个可行的迁移方案,具体预测性能由双方权重决定。为了预测T的全局最优迁移策略,我们需要用到这些边,因此taskonomy的作用是生成一系列图(如上面动图),它的参数由监督预算、选择的任务、迁移顺序和迁移函数表达构成。

创建taskonomy
taskonomy的创建过程可分为4步:I.在S中,训练针对特定任务的神经网络;II.源任务和目标任务间的所有可迁移元素都已经训练好了,用多输入任务对一输出任务训练一个高阶迁移函数;III.用AHP(层次分析法)获得归一化的迁移相关性;IV.用BIP(二元整数规划)查找全局迁移taskonomy。
任务词典
如下图所示,任务词典中一共有26种计算机视觉任务,涵盖2D、2.5D、3D和语义任务等常见主题。需要注意的是,这个词典应该是所有可以想象的视觉任务的采样集,而不是详尽的列表。采样允许我们稀疏地模拟视觉任务的密集空间,并依靠假设把成果推广到词典以外的任务中。采样空间越规则/越好,成果的通用性就越好。

任务词典
数据集
论文作者制作了一个室内场景的大型高质量数据集:
通过对齐的网格记录像素级的几何信息;
通过蒸馏从ImageNet、MS COCO和MIT Places图像中提取语义信息;
一致的摄影角度,相机功能完整;
高清晰度的图像;
是ImageNet的3倍。
这个数据集大小有12TB,如果读者有使用的兴趣,可直接联系作者申请:zamir@eecs.berkeley.edu / zamir@cs.stanford.edu。
步骤1:特定任务建模
为S中的每个任务训练一个专用的神经网络(完全监督),这些特定网络有一个均匀的encoder-decoder架构,其中编码器很大,能提取强大的表征;解码器相对较小,但足以实现良好的性能。
步骤2:迁移模型
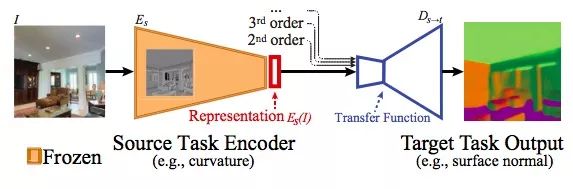
给定一个源任务s和一个目标任务t,其中s∈S,t∈T,如上图所示,从输入任务s和输出任务t中,我们的迁移网络应该能学到一些有关迁移函数的知识。其中,编码器从图片I中提取的表征是Es(I),输出函数Ds→t中包含参数θs→t,它的目标是使损失Lt最小:

其中ft(I)是t对于图像I的真值,因为Es(I)可能无法基于t和s的相关性,完美地解决任务t,所以函数Ds→t就为两者的相关性提供了一个可用的参考指标。
步骤3:用AHP进行归一化处理
既然已经获得了任务间的相关性,我们自然希望能建立一个跨任务的、具有可传递性的相关性矩阵。对于这个目标,如果只是简单地把Ls→t汇总到矩阵中,那显然是有问题的,因为它们跨度太大,而且处于不同的任务空间中,因此适当的归一化是必须的。
这里我们不能直接把它线性缩小到[0, 1]内,因为损失-性能曲线是未知的,这样粗暴的缩小没有效果。论文采用的是一种序数方法,它把输出性能和损失假设为单调变化,这之后,对于每个t,Wt是迁移到t的所有可行源任务的成对矩阵。(i, j)处的值是保留测试集中图像的百分比,即Dtest,其中si迁移到t比sj迁移到t更优(Dsi→t(I) > Dsj→t(I))。
对矩阵Wt做拉普拉斯平滑,把阈值控制在[0.001,0.999],然后计算Wt' = Wt/WtT,这样矩阵就能量化si和sj的差距,显示两者的倍数关系:
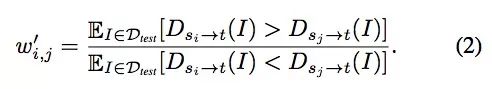
步骤4:计算全局Taxonomy
现在已经有了归一化的相关性矩阵,我们还需要制定一项全局迁移策略,最大限度地提高所有任务的集体性能,同时尽量减少所用的监督。这个问题可以表示为子图选择,其中任务是节点,传输是边。最佳子图选择理想源节点和从这些源任务到目标任务的最佳边,同时满足源节点数量不超过监督预算。
对于这个问题,论文使用的方法是布尔整数规划(BIP),详情这里不再具体介绍。

BIP计算出的关系图
实验
在论文正文中,作者没有明确给出自己的模型和其他state-of-art模型的具体对比情况,他们在附录(taskonomy.stanford.edu/taskonomysuppCVPR2018.pdf)和FCRN做了对比,发现两者在性能上并没有多大差距,但因为论文模型掌握了任务底层结构知识,在迁移上更加得心应手,使用的标记数据更少,用时也更短。

小结
本文提出了一种利用迁移学习对计算机视觉任务空间进行建模的方法,并展示了它在减少标记数据量方面的实用性。任务空间本身就是一个有趣的研究对象,但本文的研究还只是皮毛。对于这个框架,论文作者还提出了一些应注意的假设:
Model Dependence:尽管本文验证了成果在各种架构和数据集上的稳定性,但这不意味着它是万能的,它在原则上还是只适用于特性模型和特定数据。
Compositionality:本文通过一组常用的人工定义的计算机视觉任务来进行建模,那么在此基础上的进阶做法应该是把这些任务作为观察样本,进一步探究它们和其他冷门任务的相关性。
Space Regularity:本文通过一个采样词典对密集空间进行建模,尽管它表现出了良好的通用性,但为了证实这种通用性,我们还需要对计算空间的属性做更严谨的研究。
Transferring to Non-visual and Robotic Tasks:既然迁移学习在计算机视觉任务中能找出任务空间的底层结构,那它在其他领域的任务中应该也有用武之地,比如机器人研究,也许它能被用于解决机器人对下游任务的感知问题。
Lifelong Learning:在终身学习问题中,系统是不断演变的,任务数量也是不断增加的,对于这类情况,本文的一次性建模方法就不再适用了,它需要考虑更多的新因素。
-
迁移学习训练网络2019-09-09 1720
-
迁移学习2022-04-21 11310
-
cv::bmcv::resize看代码底层调用的是bmcv_image_resize,cv::resize用的是cpu吗?2023-09-18 475
-
面向NLP任务的迁移学习新模型ULMFit2018-08-22 6041
-
迁移学习、多任务学习领域的进展2018-09-04 4461
-
对深度迁移学习的当前研究进行了回顾和分类2018-09-17 7971
-
面向自然语言处理的神经网络迁移学习的答辩PPT2019-03-02 3427
-
迁移学习与模型预训练:何去何从2019-07-18 8599
-
迁移学习的意图识别在口语理解中的应用2021-04-12 936
-
基于特征和实例迁移的加权多任务聚类算法2021-06-07 750
-
一种基于标签比例信息的迁移学习算法2022-03-30 790
-
迁移学习Finetune的四种类型招式2022-04-02 4108
-
周三研讨会预告 | 从 CUDA 到 CV-CUDA:如何为自己定制高效的 CV 任务算子2023-06-13 972
-
一文详解迁移学习2023-08-11 7748
-
迁移学习的基本概念和实现方法2024-07-04 4570
全部0条评论

快来发表一下你的评论吧 !

