

L2损失函数的效果是否真的那么好呢?其他损失函数表现如何?
电子说
描述
尽管早在上世纪80年代末,神经网络就在手写数字识别上表现出色。直到近些年来,随着深度学习的兴起,神经网络才在计算机视觉领域呈现指数级的增长。现在,神经网络几乎在所有计算机视觉和图像处理的任务中都有应用。
相比各种层出不穷的用于计算机视觉和图像处理的新网络架构,这一领域神经网络的损失函数相对而言并不那么丰富多彩。大多数模型仍然使用L2损失函数(均方误差)。然而,L2损失函数的效果是否真的那么好呢?其他损失函数表现如何?下面我们将简单介绍常用的图像处理损失函数,并比较其在典型图像处理任务上的表现。
L1、L2损失函数
最容易想到的损失函数的定义,就是逐像素比较差异。为了避免正值和负值相互抵消,我们可以对像素之差取绝对值或平方。
取绝对值就得到了L1损失函数:
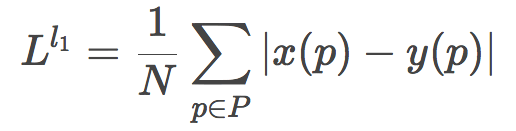
取平方则得到了L2损失函数:
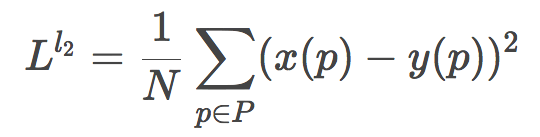
和L1相比,L2因为取平方的关系,会放大较大误差和较小误差之间的差距,换句话说,L2对较大误差的惩罚力度更大,而对较小误差更为容忍。
除此之外,L1和L2基本上差不多。
实际上,Nvidia的研究人员Hang Zhao等尝试过交替使用L1和L2损失函数训练网络(arXiv:1511.08861v3),发现随着训练的进行,在测试集上的L2损失都下降了。
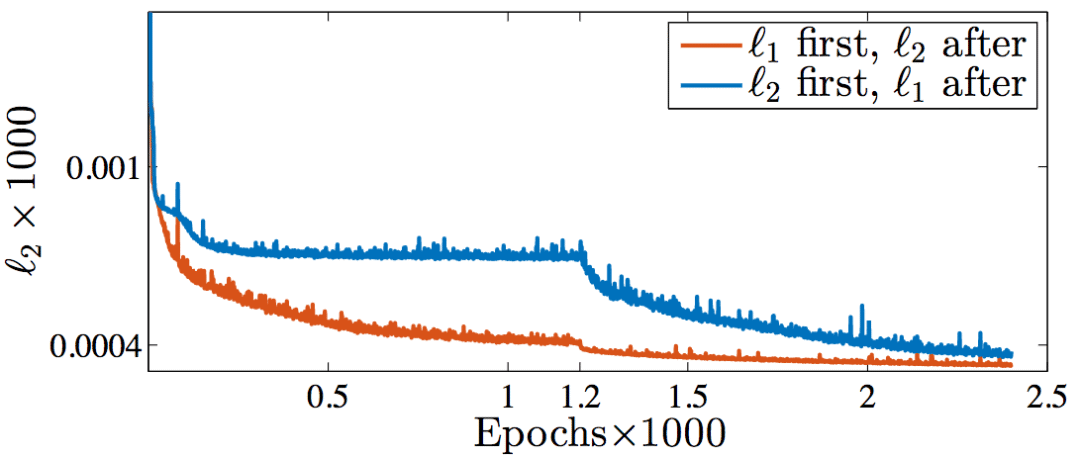
橙:前半段L1、后半段L2;蓝:前半段L2、后半段L1
顺便提下,从上图可以看到,前半段L2损失陷入了局部极小值。
不管是L1损失函数,还是L2损失函数,都有两大缺陷:
假定噪声的影响和图像的局部特性是独立的。然而,人类的视觉系统对噪声的感知受局部照度、对比、结构的影响。
假定噪声接近高斯白噪声,然而这一假定并不总是成立。
SSIM、MS-SSIM损失函数
为了将人类视觉感知纳入考量,可以使用基于SSIM或MS-SSIM的损失函数。SSIM、MS-SSIM是综合了人类主观感知的指标。
SSIM(structural similarity,结构相似性)的直觉主要是:人眼对结构(structure)信息很敏感,对高亮度区域(luminance)和“纹理”比较复杂(contrast)的区域的失真不敏感。MS-SSIM(Multi-Scale SSIM,多尺度SSIM)则额外考虑了分辨率这一主观因素(例如,高分辨率的视网膜显示器上显而易见的失真,在低分辨率的手机上可能难以察觉)。
相应地,基于SSIM的损失函数的定义为:
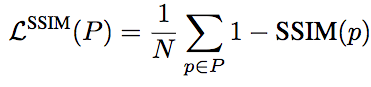
不过,由于损失函数通常配合卷积网络使用,这就意味着计算损失函数的时候其实只用计算中央像素的损失,即:
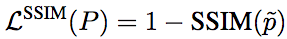
通过上述中央像素损失函数训练所得的卷积核,仍将应用于图像中的每个像素。
同理,基于MS-SSIM的损失函数为:
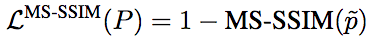
另外,我们知道,损失函数除了要准确地表达模型的目标之外,还需要是可微的,这样才能通过基于梯度下降的方法在反向传播阶段训练。显然,L1和L2是可微的。
事实上,基于SSIM和MS-SSIM的损失函数也同样是可微的。这里省略具体的推导过程,直接给出结论。
对基于SSIM的损失函数而言:
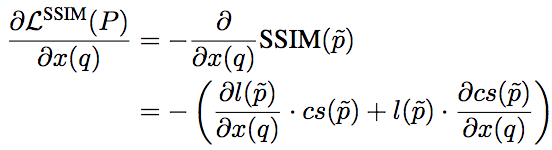
其中,l和cs分别为SSIM的第一项和第二项,其梯度为:
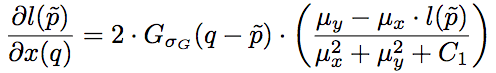
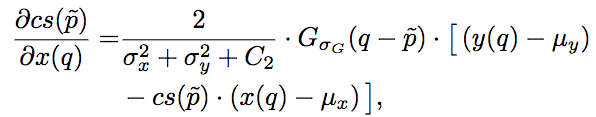
其中,Gσ_G为像素的高斯系数。这里我们看到,尽管之前的损失函数只考虑了中央像素,但因为在计算梯度的时候,实际上需要像素的高斯系数,因此误差仍然能够反向传播至所有像素。
相应地,基于MS-SSIM的损失函数的梯度计算公式为:
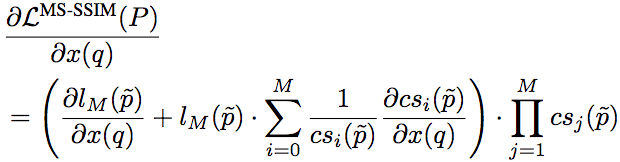
不过,由于基于MS-SSIM的损失函数需要在每个尺度上都重复算一遍梯度,会大大拖慢训练速度(每一次迭代都相当于M次迭代),因此实践中往往转而采用某个逼近方法计算。例如,使用M组不同的Gσ_G值作为替代,每组值为前一组的1/2.
评测
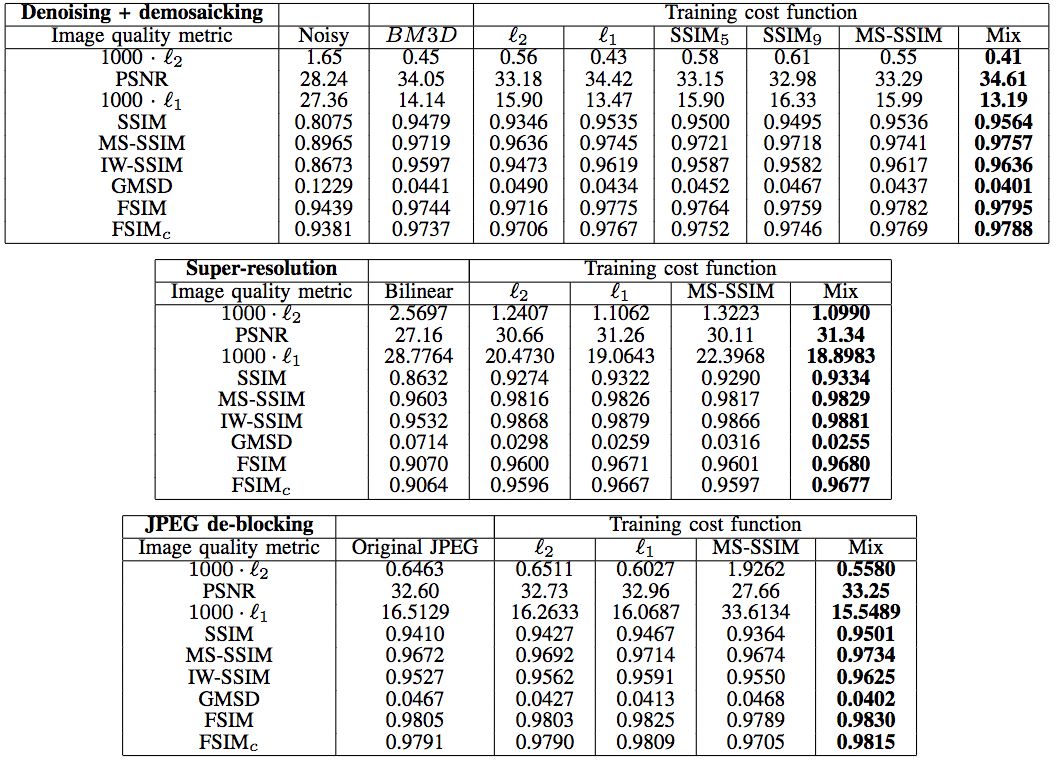
Hang Zhao等在JPEG去噪、去马赛克,超分辨率重建,JPEG去区块效应等场景对比了不同损失函数的效果。
去噪、去马赛克
上图中的BM3D代表CFA-BM3D,为当前最先进的降噪算法。我们看到,在天空这样的平坦区域(d),L2损失函数出现了污迹失真(splotchy artifact)。
超分辨率
仔细观察下图蝴蝶翅膀的黑带处,可以看到L2出现了光栅失真(grating artifacts)。
同样,下图女孩的面部,也可以观察到L2的光栅失真。
去区块
仔细观察建筑物边缘的区块,可以看到L1比L2去区块效果要好。
天空区域的区块效应更明显,相应地,L1在去区块方面表现优于L2这点就更明显了。
更多去区块的例子印证了我们上面的观察。
混合损失函数
你应该已经注意到了,上面的对比图中有一个“Mix”,而且事实上它是看起来效果最好的那个。这个“Mix”其实是Hang Zhao等提出的混合了MS-SSIM和L1得到的损失函数:
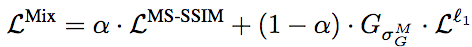
这个混合损失函数的定义很简单,基本上就是MS-SSIM和L1的加权和,只不过因为MS-SSIM反向传播误差时需要用到G高斯分布参数,因此在L1部分也分素相乘相应的分布参数而已。
Hang Zhao等经过一些试验,将α定为0.84,使两部分损失的贡献大致相等(试验发现,α的微小变动对结果的影响不显著)。
以上我们已经从视觉上演示了MS-SSIM+L1混合损失函数效果最佳。定量测试也表明,在多种图像处理任务上,基于多种图像质量指标,总体而言,混合损失函数的表现最好。
网络架构
上述试验所用的网络架构为全卷积神经网络(CNN):
输入为31x31x3.
第一个卷积层为64x9x9x3.
第二个卷积层为64x5x5x64.
输出卷积层为3x5x5x64.
内卷积层的激活函数为PReLU。
数据集
训练集取自MIT-Adobe FiveK数据集,共700张RGB图像,尺寸调整为999x666. 测试集取自同一数据集,共40张图像。
结语
总结一下以上评测:
在很多场景下,L2损失函数的表现并不好。有时可以尝试下同样简单的L1损失函数,说不定能取得更好的效果。
由于未考虑到主观感知,很多场景下,基于SSIM或MS-SSIM的损失函数能取得比L1、L2更好的效果。
结合MS-SSIM和L1通常会有奇效。
总之,虽然L2损失函数是用于图像处理的神经网络事实上的标准,但也不可迷信,不假思索地选用L2可能会错过更优的选择。
-
神经网络中的损失函数层和Optimizers图文解读2017-11-30 8289
-
TensorFlow损失函数(定义和使用)详解2020-07-28 0
-
keras常用的损失函数Losses与评价函数Metrics介绍2023-08-18 0
-
机器学习经典损失函数比较2018-06-13 8588
-
机器学习实用指南:训练和损失函数2018-06-29 8579
-
三种常见的损失函数和两种常用的激活函数介绍和可视化2019-05-05 7221
-
深度学习的19种损失函数你了解吗?带你详细了解2019-09-14 10831
-
计算机视觉的损失函数是什么?2020-03-13 3585
-
损失函数的简要介绍2020-04-17 3646
-
机器学习和深度学习中分类与回归常用的几种损失函数2020-10-09 6272
-
表示学习中7大损失函数的发展历程及设计思路2022-07-08 2234
-
训练深度学习神经网络的常用5个损失函数2022-10-19 870
-
对象检测边界框损失函数–从IOU到ProbIOU介绍2024-01-24 2981
-
语义分割25种损失函数综述和展望2024-10-22 720
-
RNN的损失函数与优化算法解析2024-11-15 531
全部0条评论

快来发表一下你的评论吧 !

