Google对基于循环网络的模型的改进

这一两年来，基于神经网络的图像压缩进展十分迅速。2016年，基于神经网络的模型首次取得了和JPEG相当的表现。而到了2017年，神经网络在图像压缩方面的表现已经超过了现代工业标准（WebP、BPG）。本届CVPR 2018上，就有三篇基于神经网络进行图像压缩的论文，分别来自Google、苏黎世联邦理工学院、港理工和哈工大。下面我们将介绍这三篇论文的主要内容。

Google对基于循环网络的模型的改进

2016年，Google的研究人员使用循环神经网络（一个混合GRU和ResNet的变体）在图像压缩上取得了和JPEG相当的表现。（arXiv:1608.05148）。

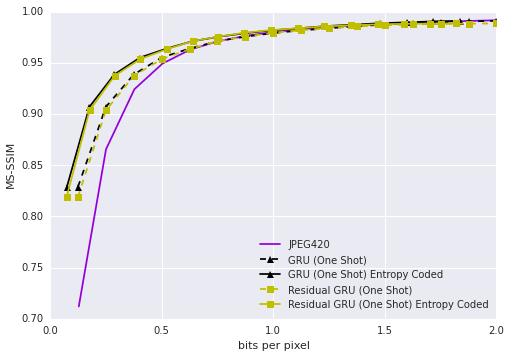
而本次在CVPR 2018上提交的论文（arXiv:1703.10114），Google对之前的模型进行了三大改进，将其表现提升至超越WebP的水平。

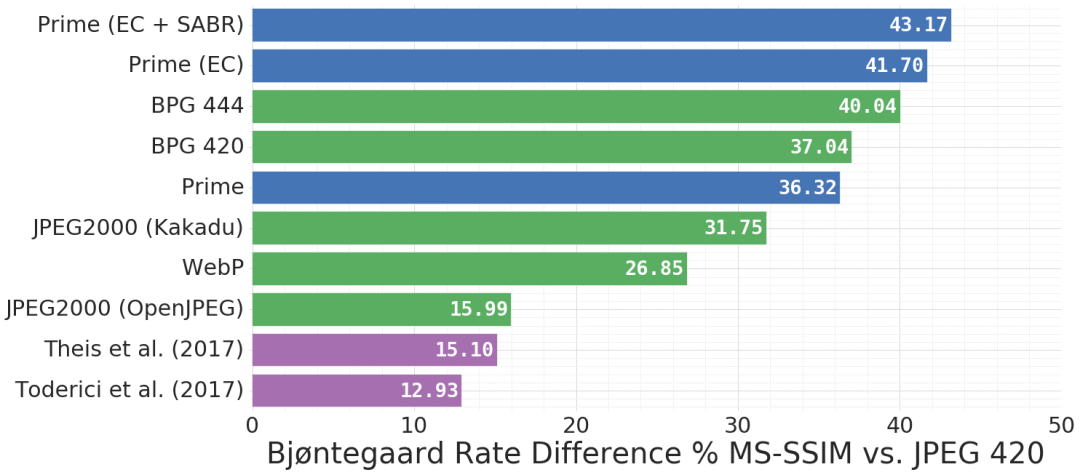
Kodak数据集上相同MS-SSIM下的压缩率比较，蓝色为Google新提出的模型

对比JPEG2000、WebP、BPG 420

网络架构

整个网络的架构和Google之前的模型类似，如下图所示：

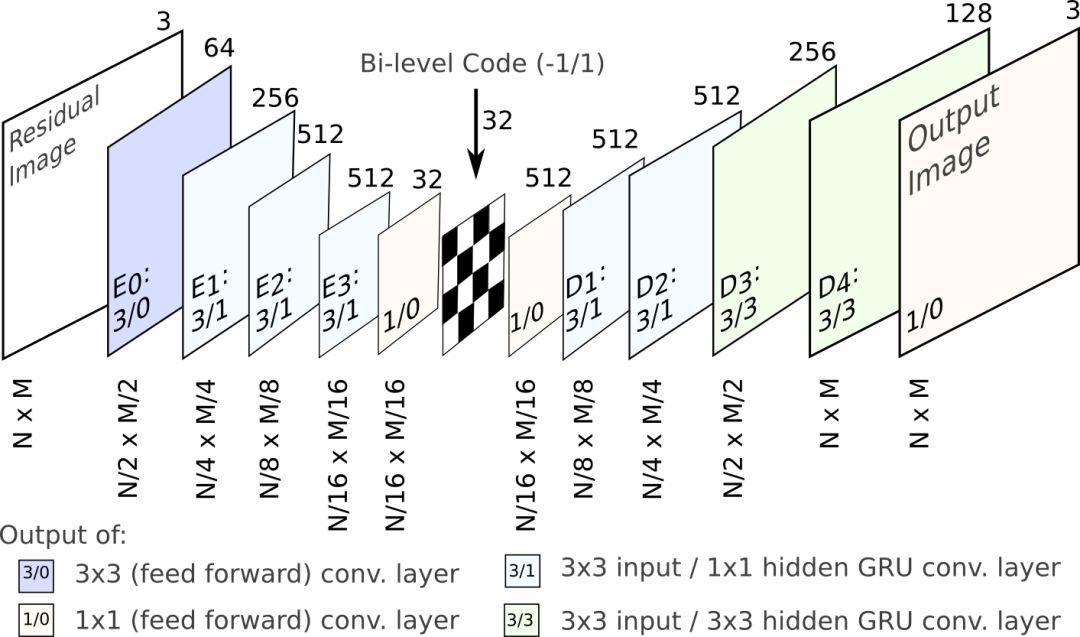
上图中，Ei为编码器，Dj为解码器，中间的国际象棋棋盘图案表示binarizer（二值化输入为1、-1）。每个网络层对应的分辨率标识于下方，深度标识于上方。其中的数字（I/H）分别表示输入（I）和隐藏状态（H）的卷积核大小。如3/1表示3x3输入卷积，1x1隐藏卷积，1/0表示1x1（前馈）卷积。另外，前馈卷积单元（H = 0）使用tanh激活，其他层为卷积GRU层。

以上示意的是单次迭代过程。在每次迭代中，上图中的循环自动编码器编码之前的重建图像和原始图像之间的残差。在每一步，网络从当前的残差中提取新信息，接着合并到循环层的隐藏状态中存储的上下文。每次迭代后，在量化瓶颈模块保存相应的比特，从而生成输入图像的渐进式编码。

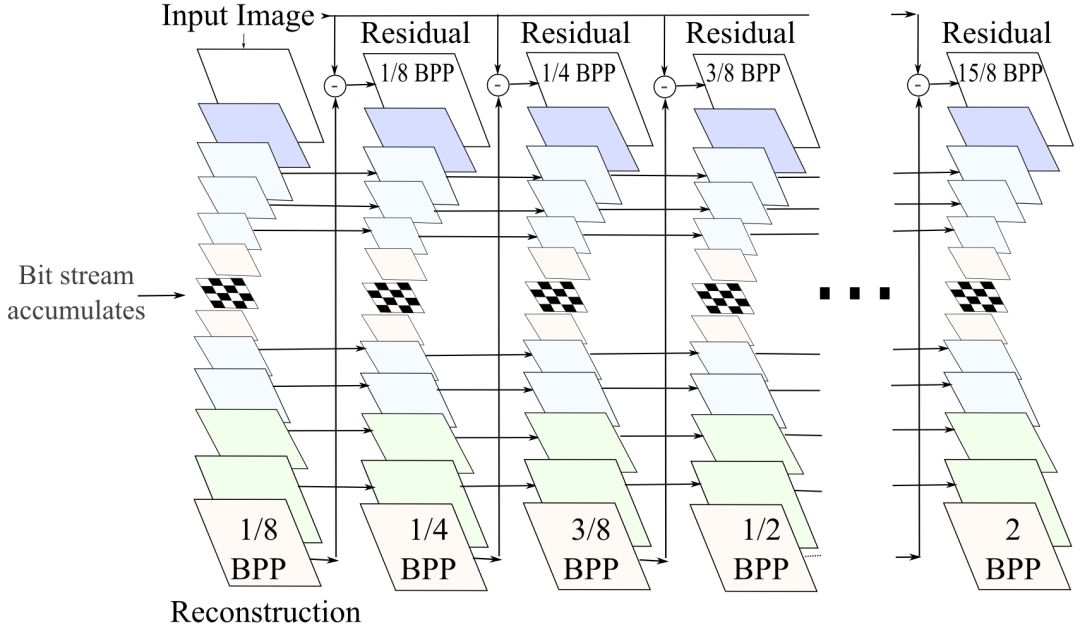
了解了模型的基本架构后，下面我们来看看Google的研究人员所做的三大改进。

隐藏状态引火

初次迭代时，每个GRU层的隐藏状态初始化为零。在试验中，Google的研究人员发现，起初的几个迭代过程中，图像质量的提升十分明显。因此，研究人员假设，缺乏一个良好的隐藏状态初始化导致模型在早期码率上表现不佳。由于编码器和解码器都堆叠了许多GRU网络层序列，编码器的binarizer和解码器的重建都需要好几次迭代才能观察到首层GRU的隐藏状态改进。因此，研究人员使用了隐藏状态引火（hidden-state priming）技术为每个GRU层生成了更好的初始隐藏状态。

所谓隐藏状态退火，或者叫“k-退火”（k-priming），单独增加了编码器和解码器网络的首次迭代的循环深度（额外增加了k步）。为了避免占用额外的带宽，这些步骤是单独运行的，编码器产生的额外位元并不会加入实际的码流。对编码器而言，这意味着多次处理原始图像，抛弃生成的位元，不过保存编码器循环单元隐藏状态的变动。对解码器而言，这意味多次生成解码图像，不过仅仅保留最终的图像重建（当然，同时保留解码器隐藏状态的变动）。

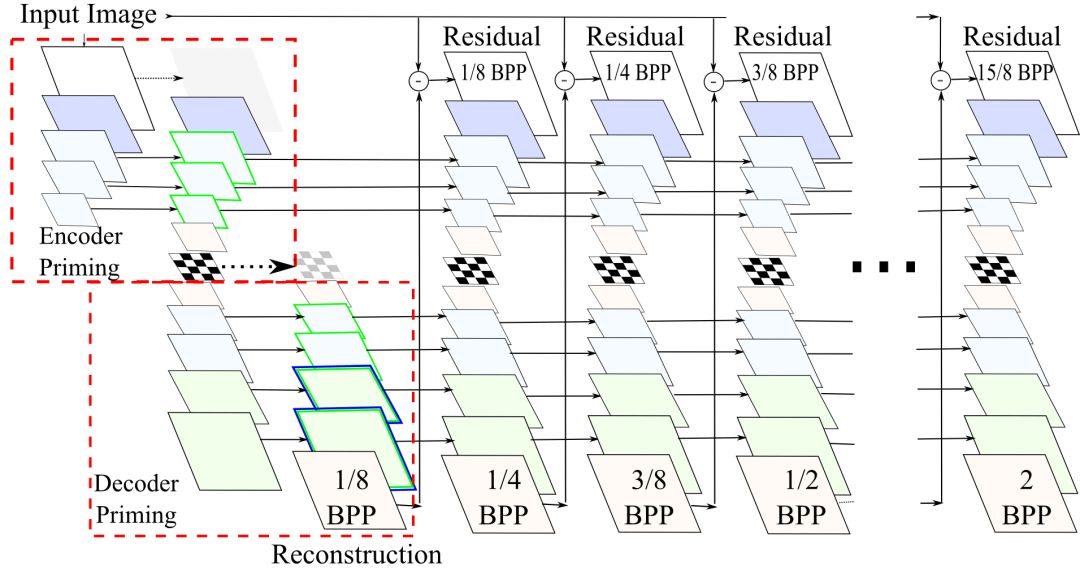
下图为网络在0.125 bpp时重建的图像对比，可以看到，引火后的重建效果明显好于未引火时。

左：原图；中：未引火；右：引火

此外，我们还可以在中间的迭代过程中进行引火，研究人员称其为发散（diffusion）。

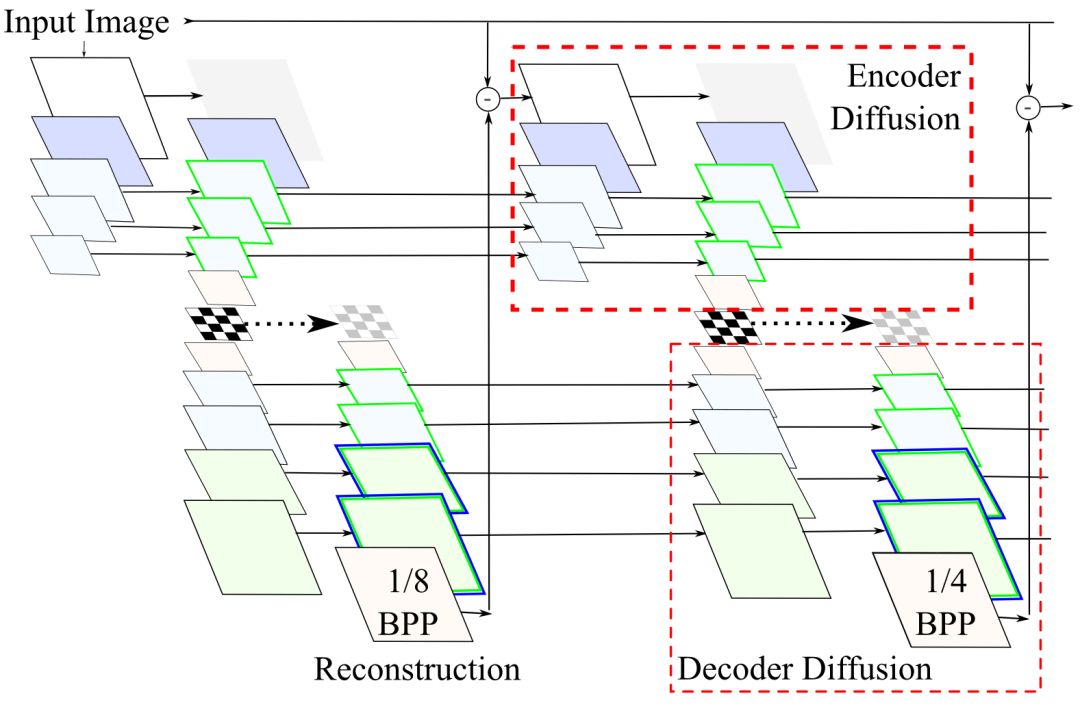
同样，我们也能从视觉上直接看出发散给图像重建带来的质量提升。

从左往右，依次为0-3次发散

空间自适应码率

如前所述，在不同的迭代中，模型生成不同码率的图像表示。然而，每张图像应用的码率是常量，而没有考虑图像的内容。实际上，图像的不同局部的复杂程度是不一样的，比如，图像上方可能是晴朗的天空，而图像下方则可能是繁复的花海。

因此，Google的研究人员引入了空间自适应码率（Spatially Adaptive Bit Rates，SABR），根据目标重建质量动态地调整局部的码率。

消融测试印证了SABR的效果：

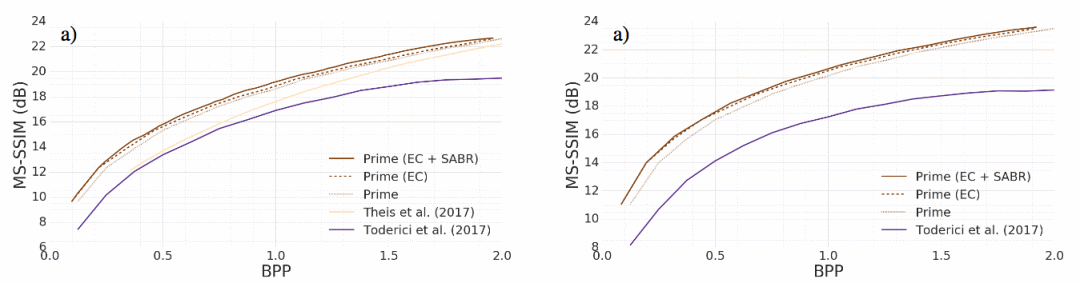
左为Kodak数据集，右为Tecnick数据集

SSIM加权损失

训练有损压缩图像网络可以说是左右为难。最直接的方式是直接比较和参考图像（即原图）像素间的差异，比如，使用经典的L1或L2损失。然而，直接比较像素差异没有考虑到主观感知因素，毕竟人眼对不同类型的像素差异（失真）的敏感程度不同。而基于感知的指标却不可微或者条件梯度不良。

为了兼顾两方面的需求，Google的研究人员提出了一种加权L1参数：

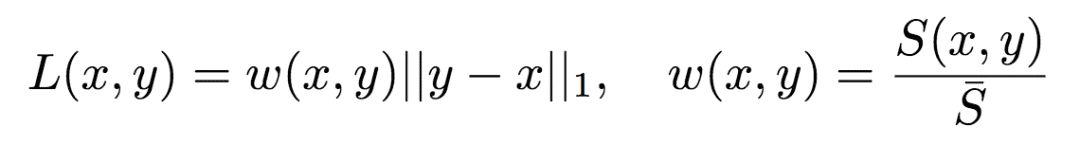
其中，x为参考图像（原图），y为fθ(x)的解压缩图像（θ为压缩模型的参数）。S(x, y)为衡量图像不相似性的感知指标，¯S为基线。具体来说，¯S为S(x, y)的移动平均。移动平均不是常量，但是在短暂的训练窗口中基本可以视作常量。在Google研究人员的试验中，移动平均的衰减为0.99. 然后，将w(x, y)视为固定值，这样就可以更新梯度了。

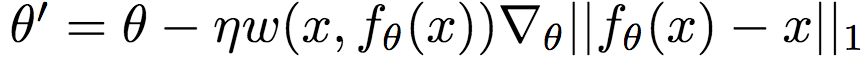
具体而言，Google研究人员使用的S(x, y)基于结构相似性指标（SSIM）。研究人员首先将图像切分为8 x 8的小块。然后在每个小块上使用以下方法计算局部权重：

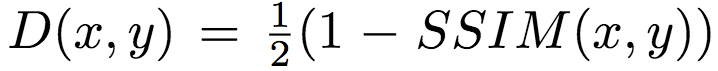
整个图像的损失为所有局部加权损失之和。

内容加权图像压缩

之前我们提到过，Google研究人员的三大改进之一是空间自适应码率（SABR），其背后的直觉是图像的不同局部复杂程度不同，应该分配不同的码率。无独有偶，香港理工大学和哈尔滨工业大学的研究人员Li、Zuo等在CVPR 2018上提交的论文“内容加权图像压缩”，同样是基于图像局部的复杂性采用不同的码率（arXiv:1703.10553）。

老鹰应该比天空占用更多的码率

SABR根据图像的重建质量调整码率，使用的是启发式的算法。而港理工和哈工大的研究人员则使用一个三层卷积网络学习图像的重要性映射（importance map），然后通过量化生成重要性掩码（importance mask），并应用于之后的编码过程。

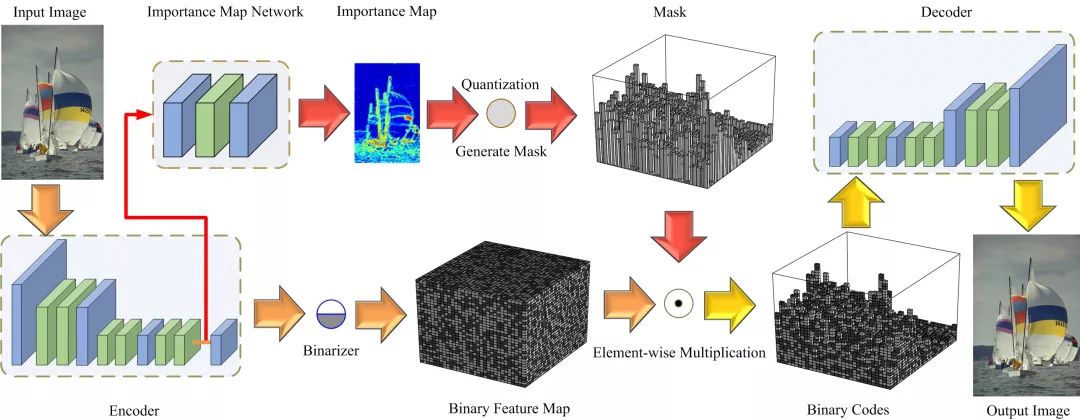
另外，模型生成的重要性映射可以适应不同的bpp。如下图所示，压缩得很厉害时，重要性映射仅仅在明显的边缘分配更多的码率。而随着bpp的升高，重要性映射给纹理分配了更多码率。这和人眼的感知是一致的。

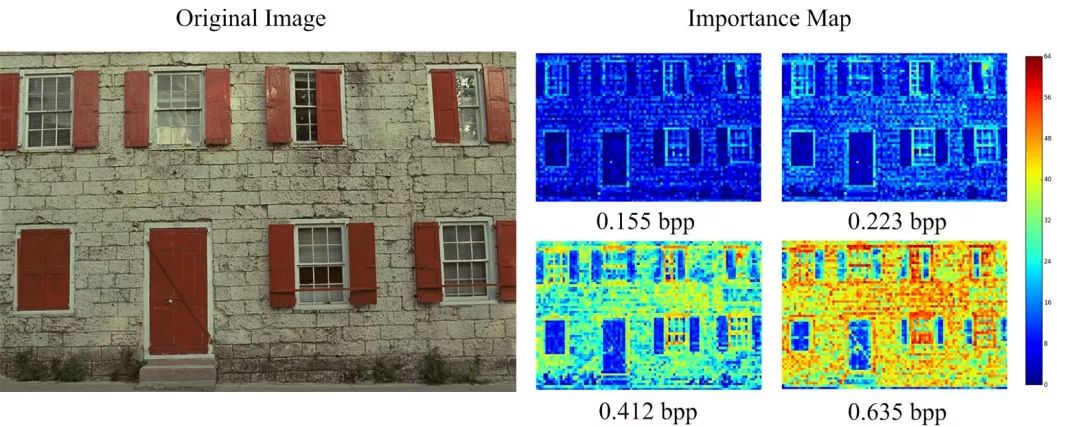
基于上下文模型并行学习

循环网络之外，基于自动编码器（auto encoder）的图像压缩模型也是一个很有希望的方向。

2017年3月，Twitter的Theis等提出了基于自动编码器的模型（arXiv:1703.00395），表现与JPEG 2000相当。

Theis等提出的压缩自动编码器架构

2017年4月，ETHZ（苏黎世联邦理工学院）的Agustsson等，提出了soft-to-hard熵最小化训练方法（arXiv:1704.00648），改进了上述自动编码器模型。2017年5月，WaveOne的Rippel和Bourdev提出的自动编码器架构使用了金字塔分解（pyramidal decomposition）编码器、自适应算术编码（adaptive arithmetic coding）、自适应码长正则化（adaptive codelength regularization），此外还使用了对抗训练（arXiv:1705.05823）。该模型的表现超越了现代图像压缩的工业标准（WebP、BPG）。

在CVPR 2018上，ETHZ的Mentzer、Agustsson等提交的论文（1801.04260），则在自动编码器的训练过程中使用一个轻量上下文模型（三维CNN）来估计潜图像表示的熵，基于熵损失并行学习，从而更好地控制重建误差（失真）和熵（压缩率）之间的折衷。

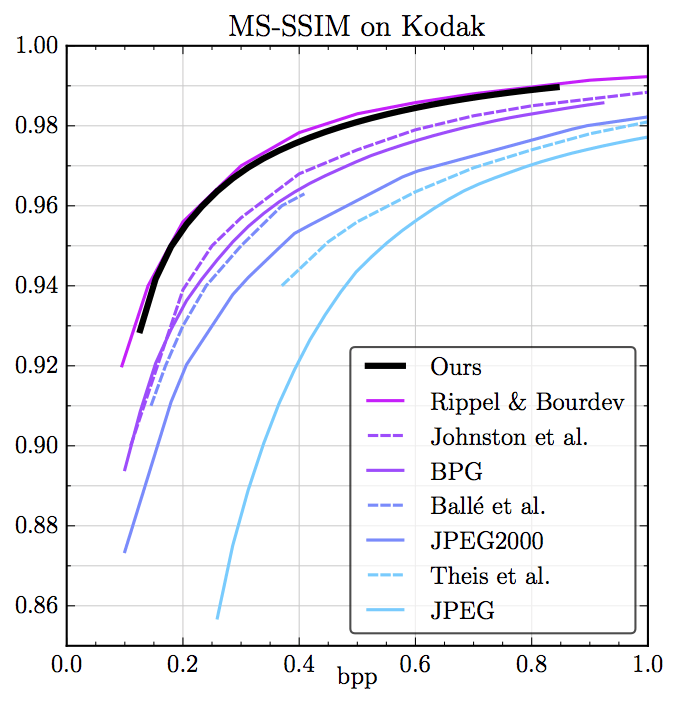
在Kodak数据集上，模型的表现超越了现代工业标准，与前述WaveOne提出的模型相当

量化

ETHZ研究人员的这项工作使用了之前提到的soft-to-hard熵最小化中的量化方法，不过对其进行了简化。研究人员使用最近邻分配计算：

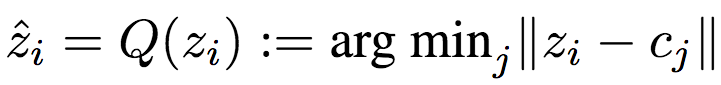
为了在反向传播阶段计算梯度，研究人员使用以下可微逼近：

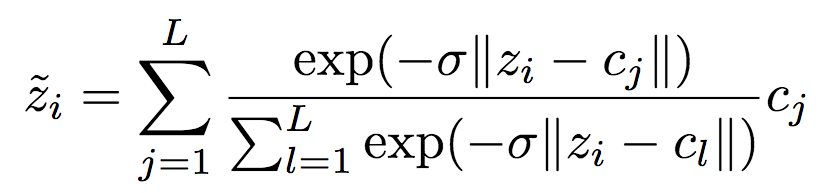
注意，以上可微逼近只在反向传播时应用，以免还要选择退火策略硬化逼近（软量化）。

模型架构

让我们看下整个模型架构的示意图。

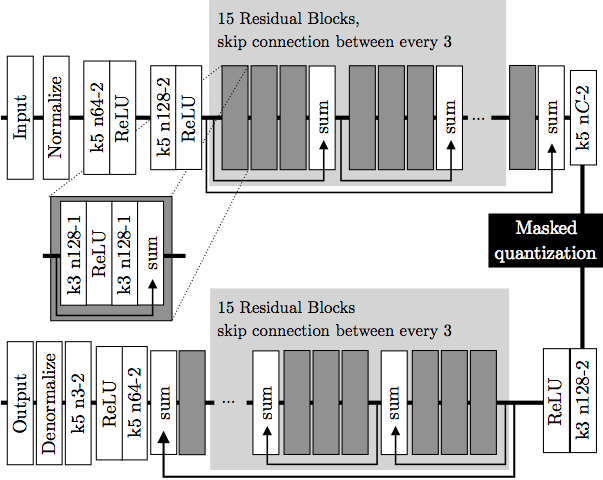
示意图上部为编码器，下部为解码器。深灰色块表示残差单元。编码器中，k5 n64-2表示核大小5、输出频道64、步长2的卷积层，其他卷积层同理。相应地，在解码器中，它表示反卷积层。所有卷积层使用batch norm和SAME补齐。Normalize表示将输入归一化至[0, 1]，归一化基于训练集的一个子集的均值和方差。Denormalize为其逆操作。Masked quantization（掩码量化）采用了之前提到过的重要性映射，不过，ETHZ简化了重要性映射的生成方法，没有使用一个单独的网络，相反，直接在编码器的最后一层增加了一个额外的单频道输出y作为重要性映射，之后将其转换为掩码：

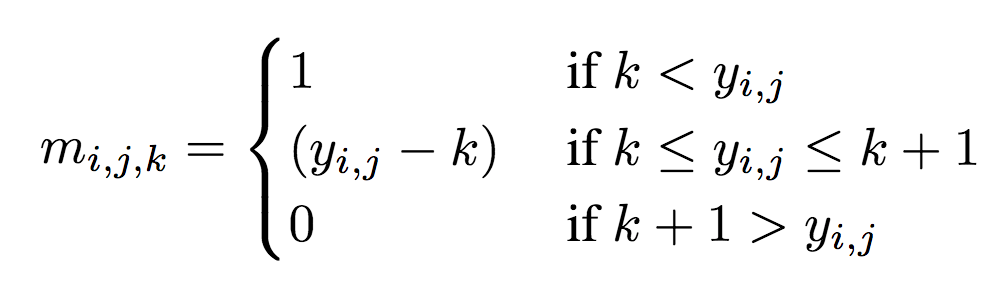
其中，yi,j表示空间位置(i,j)处y的值。k值的选取需满足掩码转换在0到1之间平滑过渡。

下图可视化了自动编码器的潜表示，可以看到重要性映射的效果：

M：加入重要性映射；M'：未加入重要性映射

整个训练过程如下：

从编码器E得到压缩（潜）表示z和重要性映射y：(z, y) = E(x)

使用刚刚提到的公式转换重要性映射y至掩码m

使用分素相乘掩码z。

量化（Q）。

使用四层的三维CNN网络计算上下文（P）。

解码（D）。

训练过程中为自动编码器（E、D）和量化器（Q）计算如下损失函数（折衷码率和失真）：

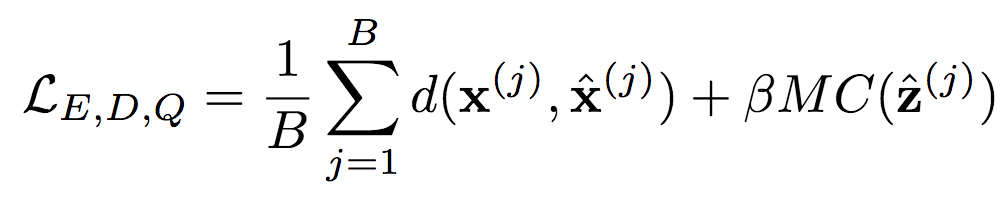
相应的上下文模型P的损失函数为：

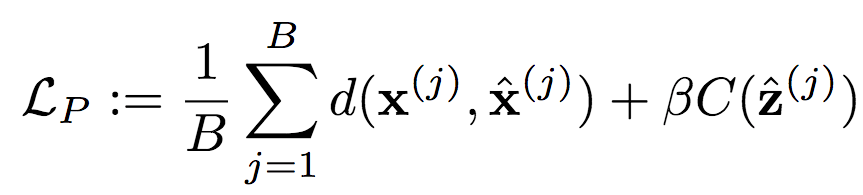
其中，C为潜图像表示的编码代价：

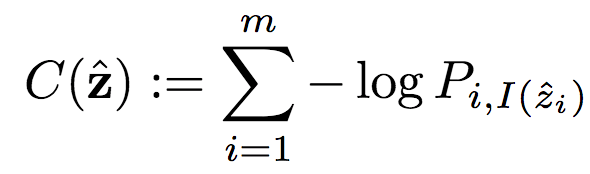
类似地，MC为掩码编码代价：

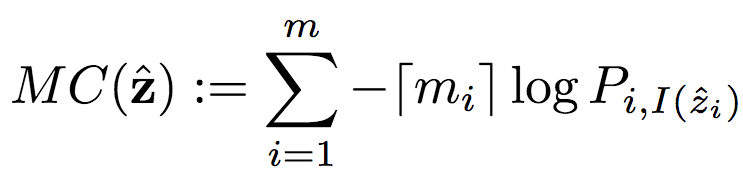
各个模型均可在GPU上并行训练。

非现实图像

ETHZ研究人员顺便测试了模型在非现实图像上的表现。

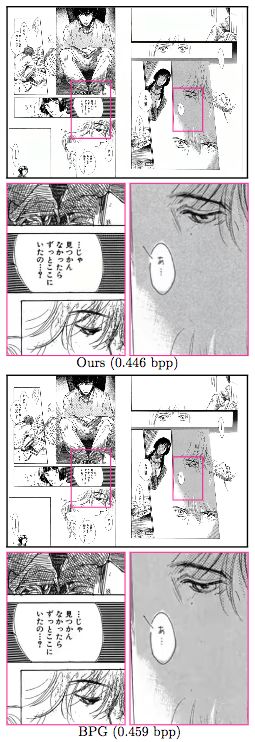
Manga109数据集样本

如上图所示，BPG压缩的黑白漫画，文字更锐利，而ETHZ研究人员新提出的模型则保留了更多脸部的细微纹理。

CLIC挑战

另外，CVPR 2018还举办了一场学习图像压缩挑战（CLIC），以鼓励这一领域的进展。

有三个团队在CLIC取得优胜，其中来自图鸭科技的TucodecTNGcnn4p在MOS和MS-SSIM两项指标上均获第一。

TucodecTNGcnn4p基于端到端的深度学习算法，其中使用了层次特征融合的网络结构，以及新的量化方式、码字估计技术。