如何找出数据集的基础结构？如何聚类和建立最有效的分组？

如何找出数据集的基础结构？如何聚类和建立最有效的分组？如何在压缩格式后有效地表达数据？这些都是无监督学习的目标。它是“无监督”的——因为你是从未经标记的数据开始的（没有Y）。

在这篇文章中，我们要探讨的无监督学习任务主要有两个，一是通过相似性把数据聚类成组，二是以降低维度的方式压缩数据，同时保持其结构和可用性。

无监督学习可能涉及的场景：

某广告平台把美国消费者细分为有类似购物习惯的较小群体，以便更精准地向他们投放广告；

Airbnb将根据社区对住房列表进行分组，以便用户能更简便地进行查询；

数据科学研究团队降低大型数据集的维度，以简化模型和控制文件大小。

与监督学习相比，我们无法提前预测无监督学习算法的具体效果，它的“表现”往往是主观的，只面向特定领域。

聚类

在现实世界中，聚类的一个典型案例是市场数据提供商Acxiom的系统Personicx，它把美国家庭分为21个生活水平群体，又在其下细分出79类不同群组。也许这看起来并没有多大用处，但对于广告商来说，这些数据成了他们在Facebook上确定广告投放地区、时间段的重要依据。

Personicx人口聚类

在白皮书中，Acxiom称系统使用的聚类方法是质心聚类和主成分分析，之后我们会对它们做简要介绍。

你可以想象，这些数据精准地切合了广告商的需求。对于迫切希望通过推送广告来达到立竿见影效果的广告商而言，他们重视的内容有两个：一是了解目标消费者的群体大小；二是通过针对消费者的人口统计特征，如兴趣爱好和生活方式，挖掘潜在的新客户。

Acxiom有一个名为“我的聚类是什么”的小工具，只需回答几个简单问题，你就能知道算法对你的分类

让我们先从聚类算法开始，慢慢了解他们是怎么做的。

k-means聚类

聚类是一种涉及数据点分组的机器学习技术。给定一组数据点，我们可以用聚类算法将每个数据点到分类到图像中的特定组中。理论上，同一组中的数据点应具有相似的属性和特征，而不同组中的数据点的属性和特征则应高度不同。

通过k-means算法，我们能把目标数据点聚类为k个簇。k值越大，簇越少，每一簇包含的数据点就越多；k值越小，簇越多，每一簇包含的数据点就越少。

该算法的输出是一堆打好了“标签”的数据点，每个标签指向数据点所属的k簇。进行聚类时，算法会根据k值为数据定义k个聚类质心点，这些质心就像是每个簇的核心，它们不断“捕捉”最接近自己的点并把它们添加进聚类中。

如果这还不够形象，那你也可以把它们想成派对舞会上出现的那些充满魅力的人，他们瞬间就能引起身边人的关注。如果这样的人只有一个，那全场人都会聚集在他身边；如果有很多个，那舞会上就会形成许多较小的活动团体。

以下是k-means聚类的简要步骤：

1. 定义k个质心。随机初始化k个质心；

2. 为质心找到最接近它的数据点并构建簇。将每个数据点分配给k个质心中的一个，分配依据是数据点和质心的接近程度，也就是欧氏距离平方和最小。

3. 更新质心位置，将它移到更新后簇的中心。计算簇中所有点的平均位置，这个得出的新向量就是质心的新位置。

k-means聚类的一个实际应用是对手写数字进行分类。假设我们有一些黑白的数字图像，图像的像素为64 × 64，每个像素代表一个维度，那么这些图像就有64 × 64 = 4,096个维度。在这个4,096维的空间中，k-means算法能把所有聚集紧密的像素点聚类成一个簇，假设它们同属于一个数字。实践证明，这种做法在数字识别上取得了非常好的结果。

层次聚类

层次聚类和常规的聚类算法大体相似，它的不同之处在于它聚类的簇具有层次结构。这对于一些有不同灵活性需求的任务来说很有用，如想象一下Amazon的网上商城，它的主页上有很多分组的商品，通过导航栏，我们能找到目标商品所属的大类，之后再是更细分的、更具体的小类。对于一些项目集群，像这样逐层提高数据颗粒密度是有价值的。

就算法的输出而言，除了聚类成各个子集，层次聚类的一个优点是可以呈现一整棵树，并由你自行选择要聚类成什么效果，比如簇的数量。

以下是参差聚类的简要步骤：

1. 定义N个簇，每个簇包含1个数据点；

2. 合并彼此最接近的两个簇，现在我们就有N-1个簇；

3. 重新计算各簇之间的距离。对于计算距离，我们有多种方法，其中一种是将两个簇之间的距离视为他们各自数据点之间的平均距离。

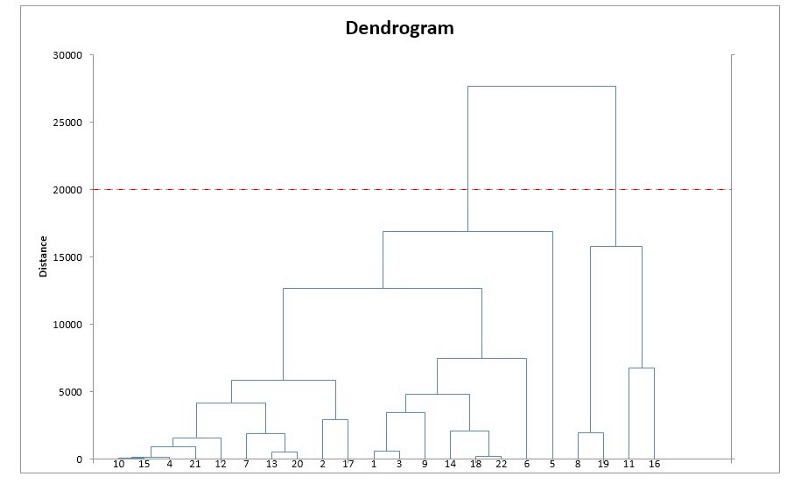
4. 重复步骤2和3，直到最后获得一个包含所有数据点的簇。这时我们得到了一棵树，如下图所示。

5. 选取多个簇并在树状图上绘制一条水平线。例：如果我们想要k = 2个簇，那就应该在distance = 20000的位置画一条线，这时我们就能得到一个包含数据点8、9、11、16的簇以及另一个簇。簇的数量等于水平线和树状图的交点数。

降维

降维听起来和压缩差不多。它是为了尽量减少数据的复杂性，同时保持尽可能多的相关结构。如果我们有一张128 × 128 × 3的图像（长×宽×RGB），它的数据维度就是49,152。这时，如果我们能在不破坏图象原有内容的前提下降低图像所在空间的维度，这对于后续计算是十分有帮助的。

让我们先通过实践看看两种用于降维的主要方法：主成分分析和奇异值分解。

主成分分析（PCA）

在开始讲解前，我们先来做一个线性代数小复习——向量空间和基。

在一个普通的平面坐标中，原点O是(0, 0)，基向量i为(1, 0)，j为(0, 1)。但事实证明，我们可以选择一个完全不同的基，比如把i'=(2, 1)和j'=(1, 2)作为基向量，这就成了另一个坐标系。如果你有耐心，你可以计算出原来iOj坐标系上的(2, 2)到i'Oj'上会变成(6, 6)。

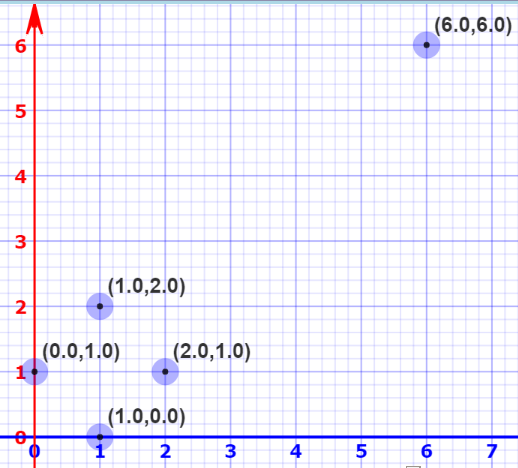
这样做的意义在于我们能改变向量空间的基，想象更高维的空间，比如5万维。选择一个基，挑选出其中最重要的200个基向量，我们把这些向量称之为“主成分”。这之后，你挑出的向量子集就能构成一个新的向量空间，它的维度比原来的更低，但保留了大部分数据复杂性。

选择最重要的主成分，考察它保留了多少差异性，然后按照这个指标进行排序。

PCA的另一个用处在于降低数据文件大小。经过重新映射后，原本的数据空间会被压缩至低维，更有利于之后的计算。

扩展阅读：Diffusion Mapping and PCA on the WikiLeaks Cable Database

地址：http://mou3amalet.com/cargocollective/675_xuesabri-final.pdf

奇异值分解（SVD）

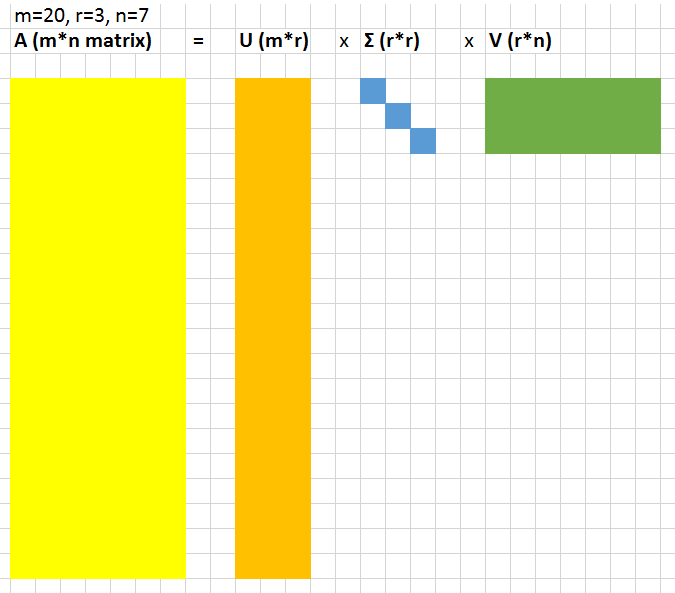
让我们将数据表示为一个较大的A = m × n的矩阵。SVD是一种计算，它允许我们将该大矩阵分解为3个较小矩阵（U = m × r，对角矩阵Σ= r × r，以及V = r × n，其中r是一个小数）的乘积。

以下是一个直观的例子。

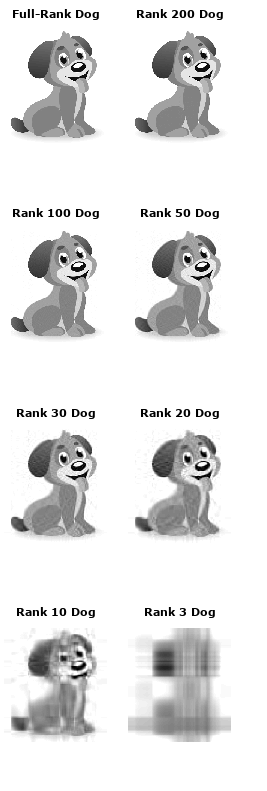
r*r对角矩阵Σ中的值被称为奇异值。它们的神奇之处在于可以用来压缩原始矩阵。如果我们在原始矩阵U和V中删除最小的20%奇异值的相关列，矩阵会缩小很多，但仍能很好地表示底层矩阵。为了更准确地展示它的效果，我们可以来看看这条狗：

首先，如果我们按照量级对奇异值（矩阵Σ的值）进行排序，则前50个奇异值包含整个矩阵Σ85％的量值。

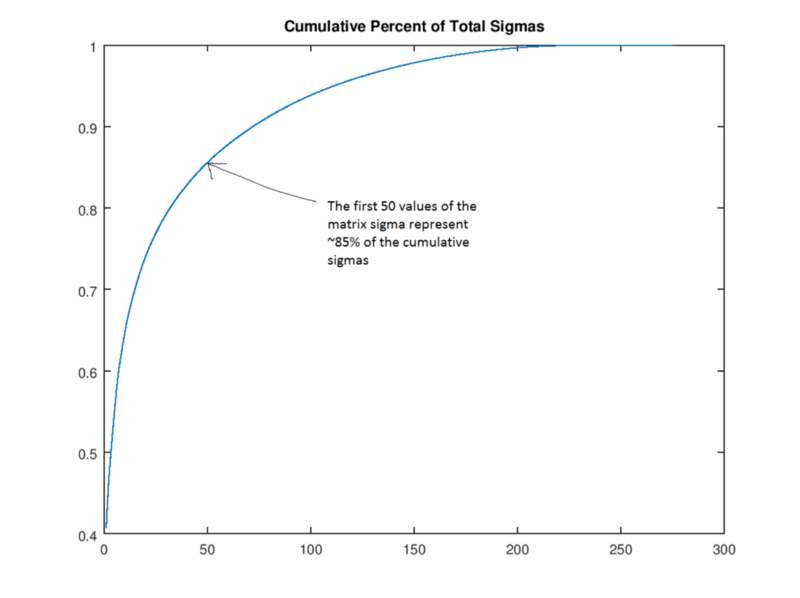
因此我们可以把矩阵Σ中剩下的250个值舍去，也就是设置为0，获得一个“rank 50”的版本。在下图中，我们分别列举了200、100、50、30、20、10和3的狗，可以看出，随着图片空间逐渐变小，它的清晰度也不断下降，但就肉眼的观察情况看，“rank 30”的图像还是表现出了很多接近原图的特征。我们可以计算这一过程中算法压缩了多少空间：原始图像矩阵有305 × 275 = 83,875个值；“rank 30”的狗则只有305 × 30 + 30 + 30 × 275 = 17,430个值（要算上矩阵U和V乘以0的量）——几乎是原图的五分之一。

实战演练和进阶阅读

k-means聚类

尝试可视化聚类过程，以建立对算法工作原理更直观的理解。你也可以参考用k-means聚类手写数字的开源项目，并学习坐着列出的各类在线教程。