如何进行声音定位？

一、人耳是如何进行声音定位的？

在当今科技高度发达的社会中，声音中蕴含的信息受到普遍关注。不论是炮弹的落点，轴承的异常啸叫，还是收音设备的自动跟随等方面，判断其声音产生的方位都是一个重要课题。

现阶段的声音定位技术大多是根据“人耳”发展而来的。人类单耳判断声源的方法是利用了耳廓对声音的反射使声波发生干涉，从而达到判断声音的目的。当然更多情况下是双耳判断方向，主要有时间差（ITD）和声级差（ILD）两种形式，我们简单解释一下。

人类两耳间的距离大约在16-18cm，时间差正是利用了这一点。当声音从左侧传来，左耳首先接收到信号，在零点几毫秒后，右耳接受到声音信号。虽然时间很短，但也能让人类判断声音产生的方向了。

声级差效应的原理与时间差类似。当声源在头部的右侧时，声波经过头部的衰减，到达左耳的声音强度就会减弱，这样人们就可以通过声音强弱辨别声音的方向了。

二、用机器代替耳朵

人耳对声源的定位精度毕竟是有限，而现实生活的需要只靠人耳已经满足不了，所以人们发明出声强探头和麦克风阵列等声源定位仪器。

声强探头可以看作是单个耳朵靠近声源在听，通过不断移动探头以确定声源的位置。更为常用的则是麦克风阵列，麦克风也叫做传声器，它相当于人的耳朵，但是比人耳要灵敏的多。在麦克风阵列上有几个到几千个麦克风，它们按照一定的规则排布构成，因此叫做麦克风阵列。麦克风感知声音的原理在我们之前的文章中介绍过，所以这里我们主要介绍它是怎样代替耳朵判断声音位置的。

三、麦克风阵列代替耳朵的原理

如何通过麦克风阵列判断声源位置呢？我们介绍一种简单的TDOA算法，它可以利用时间差进行定位，下面进行详细说明。

假定一个平面上有3个基站，分别是A1，A2和A3，而且A1、A2、A3的坐标已知，分别是（X1，Y1），（X2，Y2），（X3，Y3）。假设待定位声源Tag的位置是（x，y）。这样就可以得到待测点T到每个基站的距离：

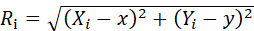
，其中i=0，1，2。

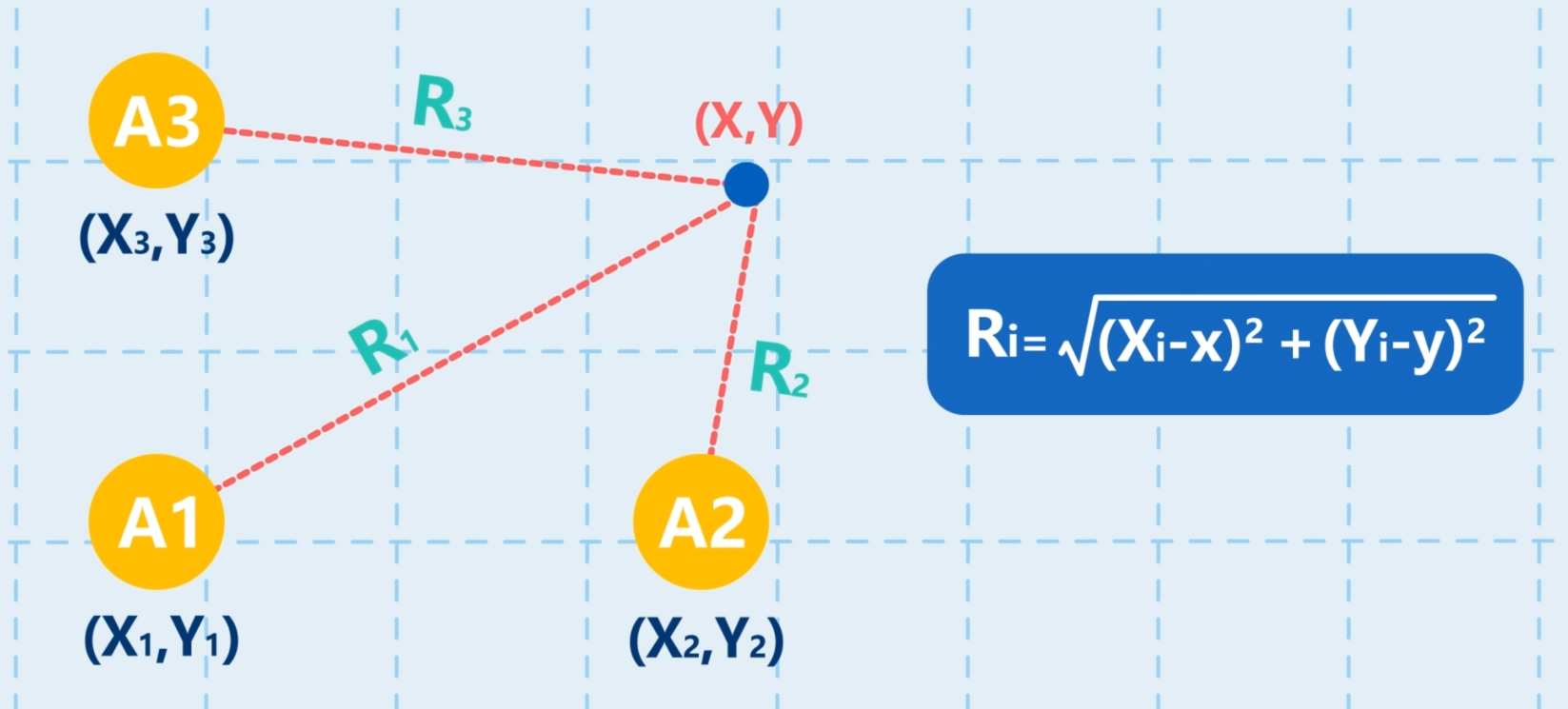
可以想到：求解点的位置，能够转化成求解两条曲线的交点，但由Ri的表达式组成的方程组显然无法求解，因为方程组中的未知量太多。不过距离差R2,1= R2-R1、R3,1= R3-R1是已知的，因为声音的传播速度已知，约为340米每秒，而且通过采集设备能够计算出声音到达各基站的时间，也就能求出距离差R2,1和R3,1了。那么有没有一种曲线与距离差有关呢？这就是双曲线。它的定义是平面上一点到两个定点的距离之差的绝对值是定值的点的轨迹，这种曲线适用于上述情景。如下图所示，（x，y）是待求解的点，到A1、A3的距离是定值可构成一条曲线，到A1、A2的距离是定值可构成一条曲线。所以在刚刚的平面上我们就能画出这样的两条曲线，而它们的交点就是我们T的位置（x，y）。那么就能列出这样的非线性双曲线方程组了。

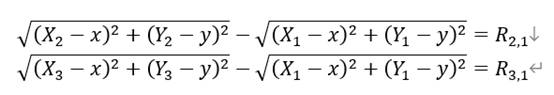
求解此方程组时，我们要尽量减少根式的存在。首先将方程组简化成：

Ri,1= Ri-R1 

所以有方程：

Ri^2= (Ri,1 +R1)^2           （1）

由

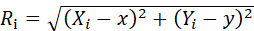
可得：Ri^2=Xi^2-2Xi*x+x^2+Yi^2-2Yi*y+y^2      （2）

将（2）式代入（1）式中

则有：Xi^2-2Xi*x+x^2+Yi^2-2Yi*y+y^2=Ri,1^2+2Ri,1*R1+R1^2

又因为：R1^2= X1^2-2X1*x+x^2+Y1^2-2Y1*y+y^2

所以可得方程：

Xi^2-2Xi*x+x^2+Yi^2-2Yi*y+y^2-(X1^2-2X1*x+x^2+Y1^2-2Y1*y+y^2) =Ri,1^2+2Ri,1*R1

令Ki=Xi^2+Yi^2化简得：

Ki-K1+2X1*x-2Xi*x+2Y1*y-2Yi*y=Ri,1^2+2Ri,1*R1

Ki-K1+2x(X1-Xi)+2y(Y1-Yi)=Ri,1^2+2Ri,1*R1

又令：Xi,1=Xi-X1、Yi,1=Yi-Y1

则有：Ki-K1-2x*Xi,1 - 2y*Yi,1 =Ri,1^2+2Ri,1*R1

通过一系列的等式变换，我们成功将未知项的二次项消除了。当i=2，3时，可得方程组

K2-K1-2X2,1*x-2Y2,1 *y=R2,1^2+2R2,1*R1

K3-K1-2X3,1*x-2Y3,1 *y=R3,1^2+2R3,1*R1

通过消元法得到

X=

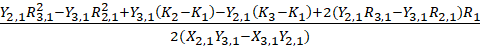
y=

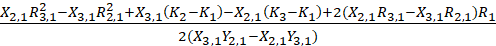
等式中的未知量只有R1，怎样求解它的值呢？

我们先简化一下上述等式，令：

p1=

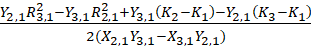
q1=

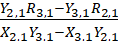
p2=

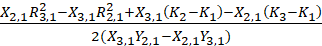
q2=

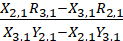
这样就得到等式

x=p1+q1*R1

y=p2+q2*R1         ……(3)

而且等式中的p1、q1、p2、q2都是已知量。再将(3)式带回到(2)式中，因为要求R1的值，所以(2)式中的i=1。可得等式：

R1^2=X1^2-2X1(p1+q1*R1)+(p1+q1*R1)^2+Y1^2-2Y1(p2+q2*R1)+( p2+q2*R1)^2

化简得：

(q1^2+q2^2-1)R1^2-2[q1(X1-p1)+q2(Y1-p2)]R1+[(X1-p1)^2+(Y1-p2)^2]=0

这样就得到一个关于R1得一元二次方程，用求解公式R1=

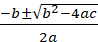
解出R1，然后将有效解带入到(3)式中就可以求出x、y的值了。

这种TDOA算法较为简单，没有考虑到可能出现的误差，同时参考基站的数量也比较少，所以会导致定位不精确。

四、声源定位实验

下面我们正式开始实验，使用三个麦克风声音传感器组成一个平面直角坐标系，X1麦克风为原点，距X2麦克风15cm，距X3麦克风27cm。麦克风需要5V的直流电源，我们将它的输出端S与USB-5111采集卡的Ai端口连接，GND端连接到采集卡的AGND端口上，VCC端与电源正极连接。电源的负极与采集卡的AGND连接。最后将采集卡与电脑连接。

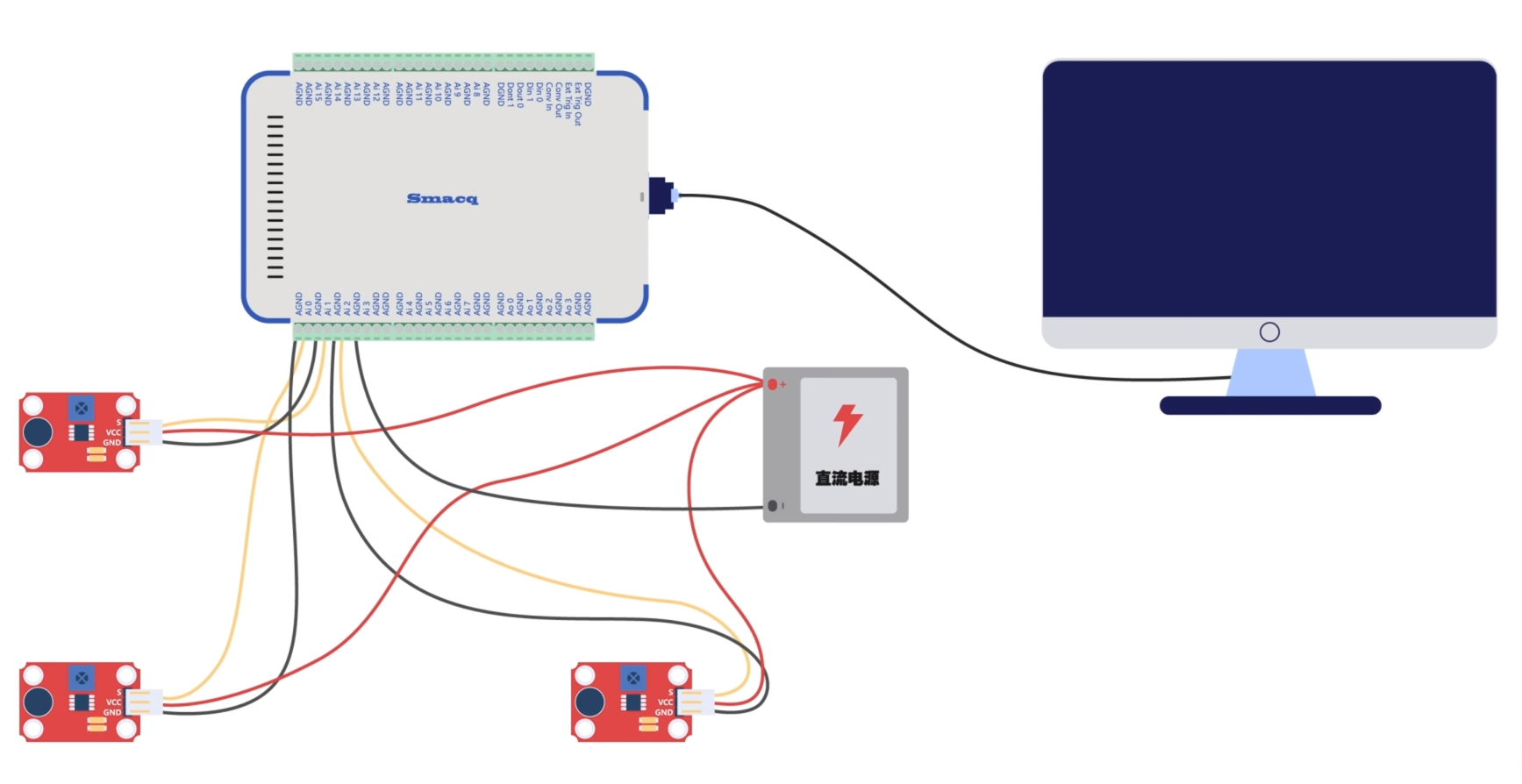
接下来我们打开Smacq DAQ软件采集声音信息。开启Ai0、Ai1，Ai2通道，

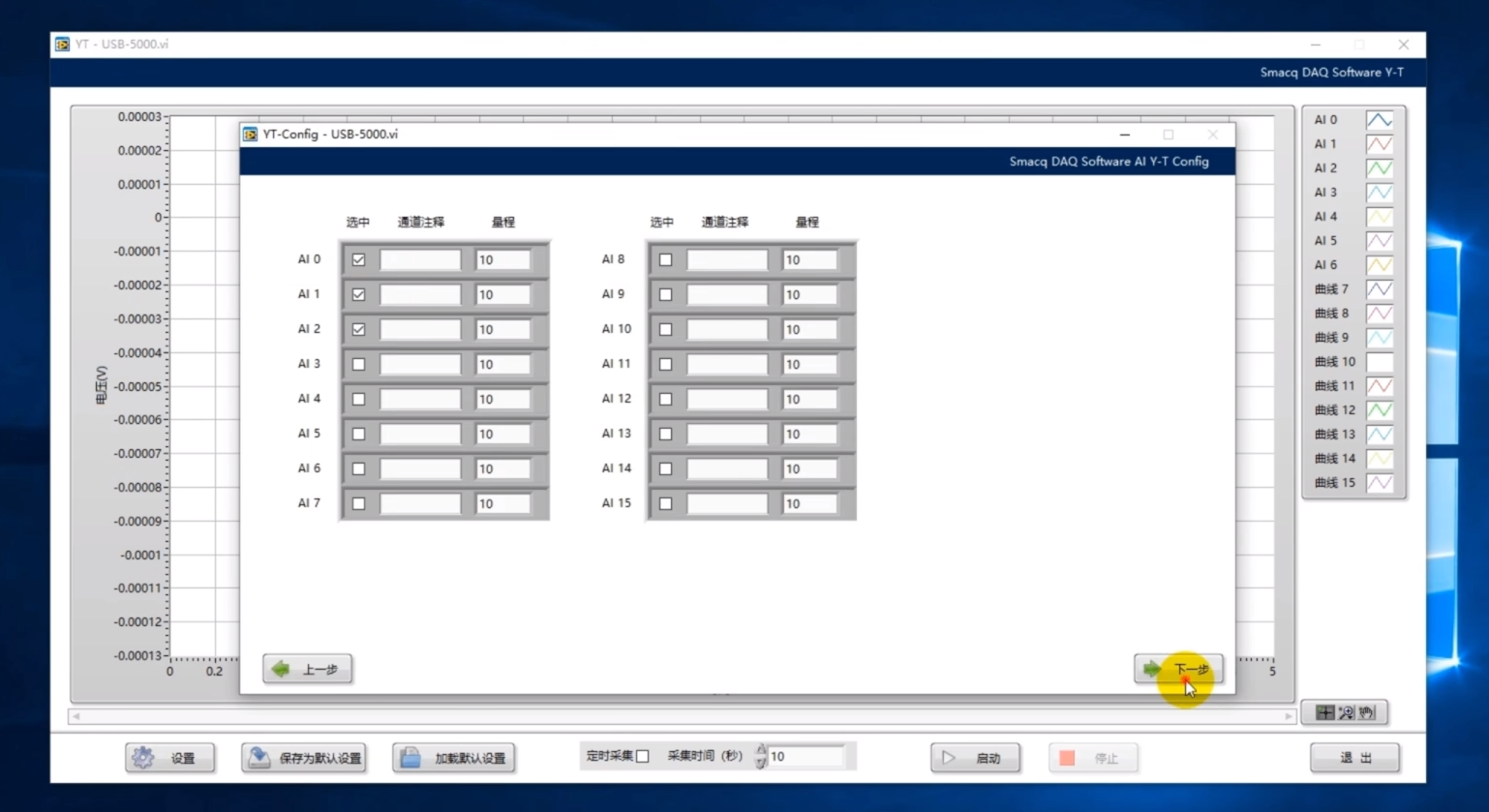
设置采集卡的采样率为100000（Sa/s/ch），其他设置保持默认就可以了。

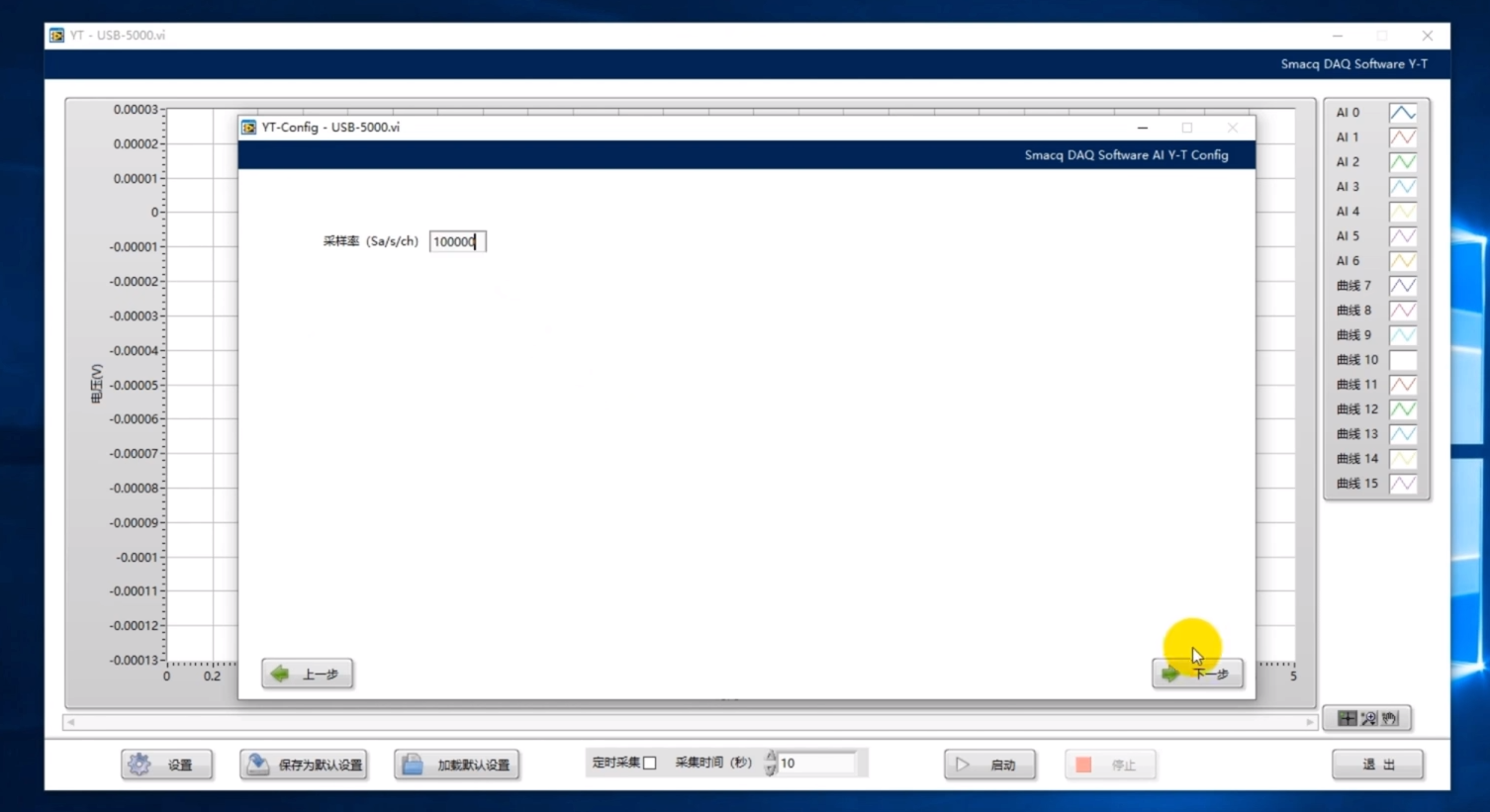
点击启动，在靠近X1传感器的位置拍手后，点击软件的停止按钮。

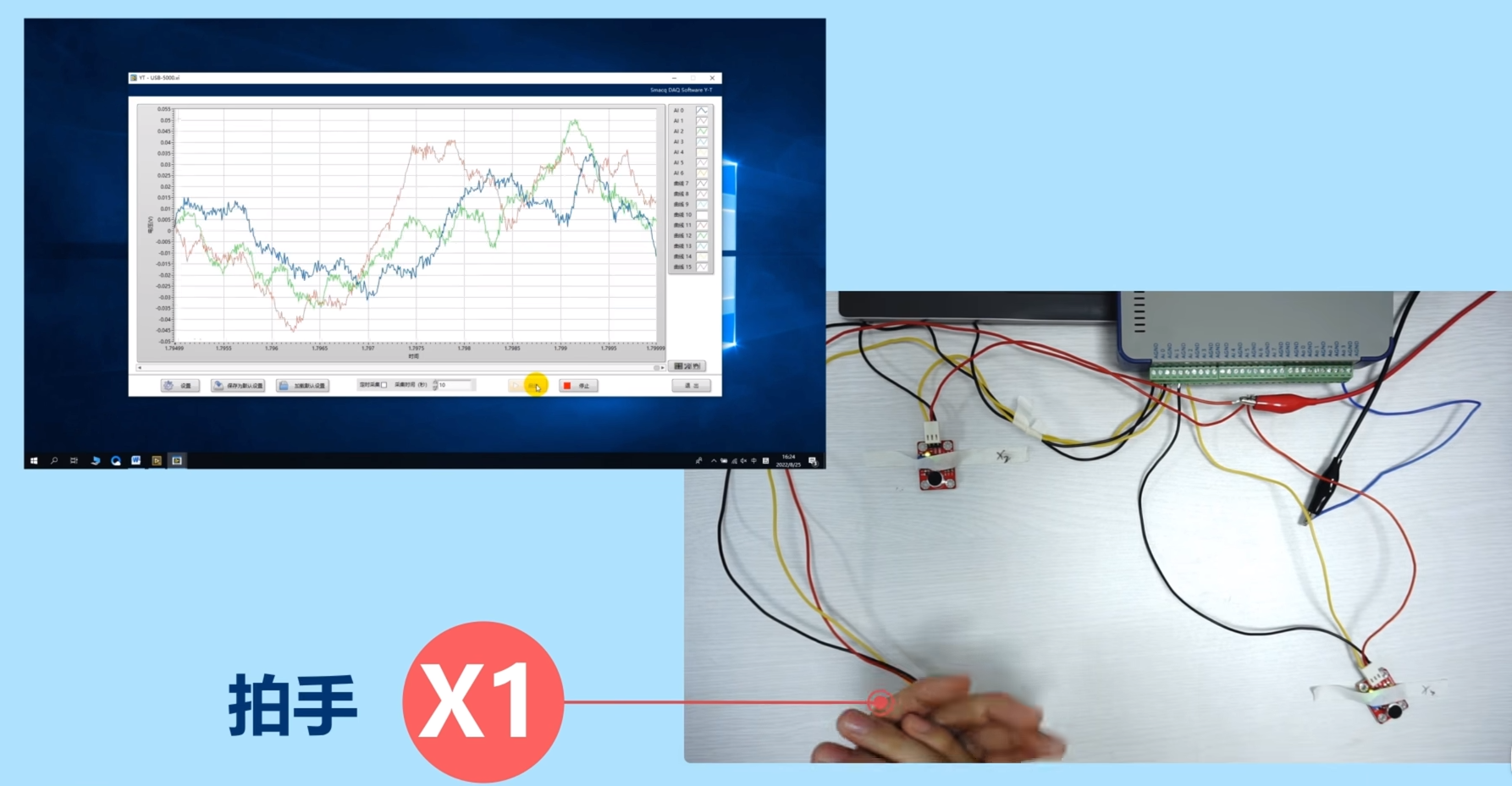
使软件显示全部的采集波形，选择一组反应较为明显的波形，将它的时间信息输入到计算声源位置程序中，

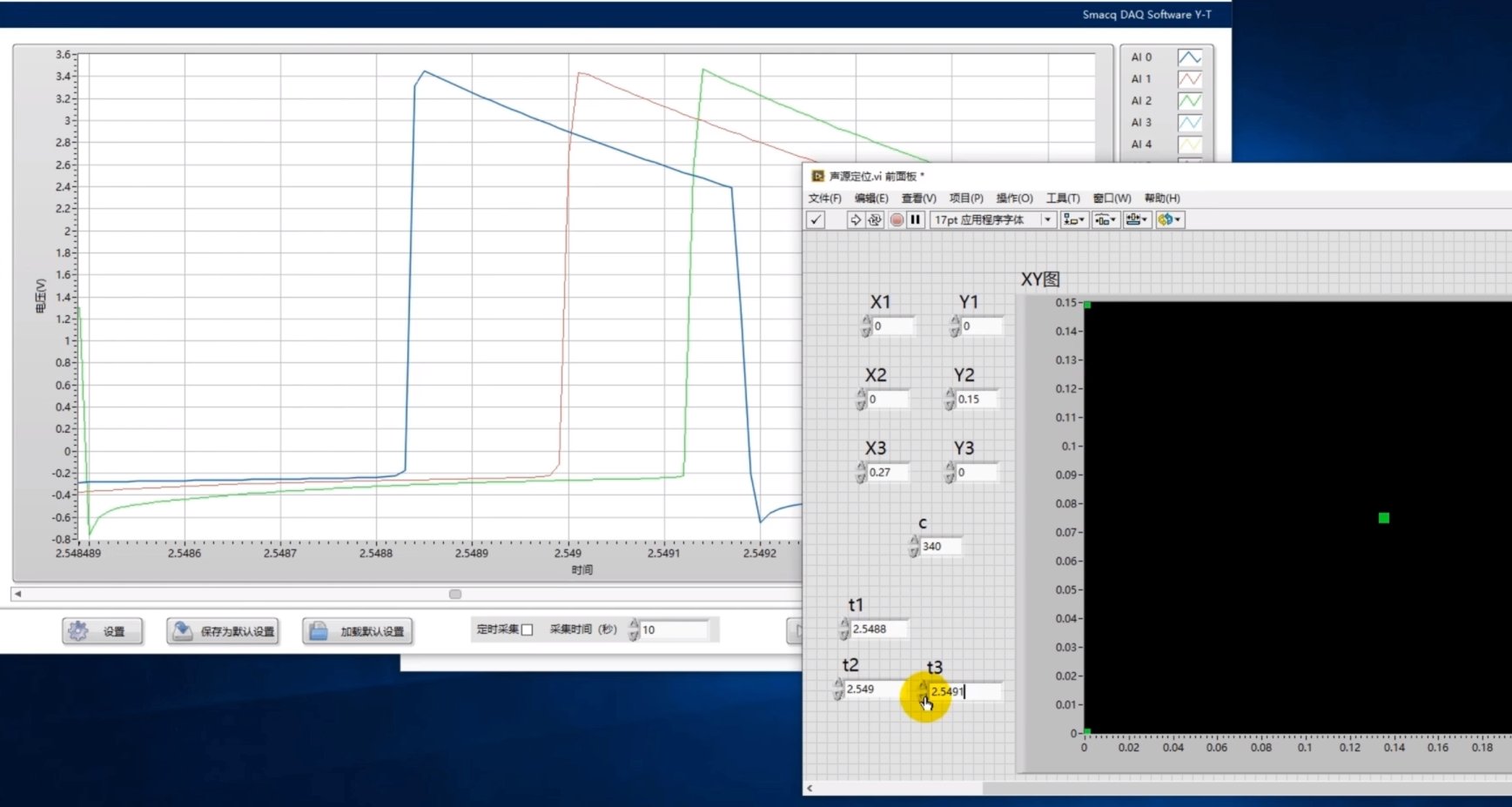
点击运行后，我们就可以看到声源点出现在靠近X1坐标的位置。

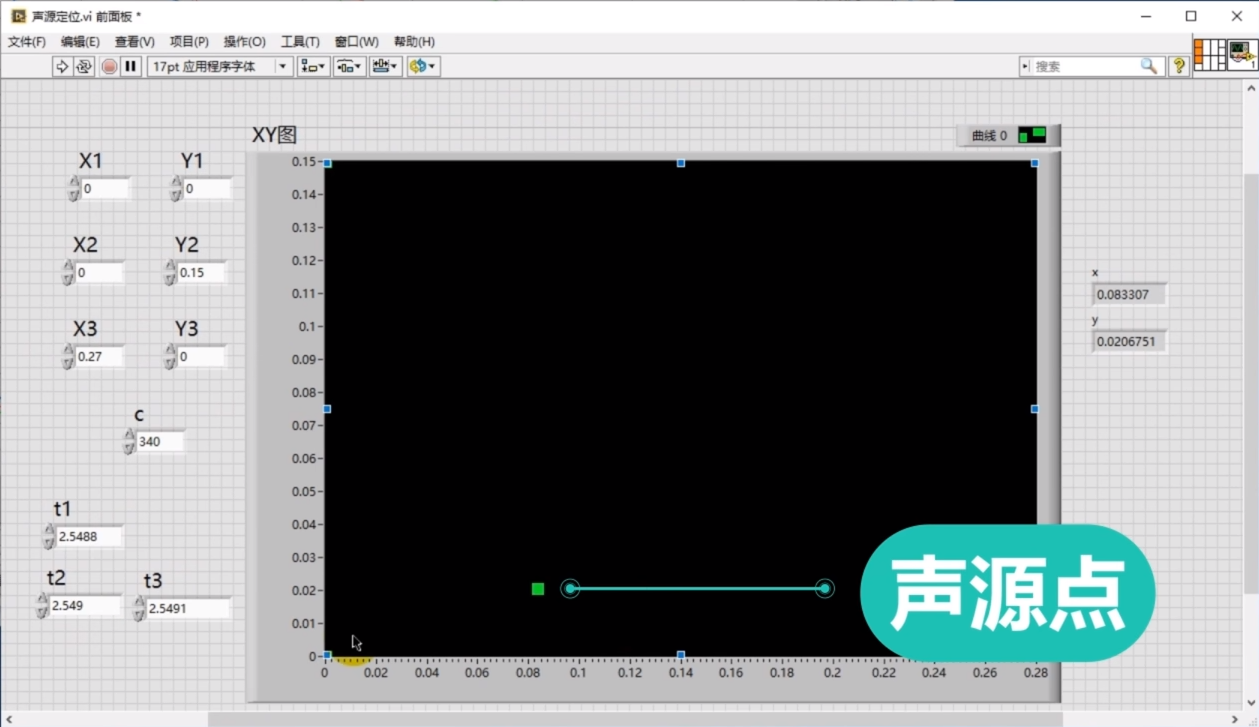
以上内容就是我们声源定位实验的全部内容。如果大家对文章内容有任何问题，欢迎在评论区留言或搜索微信公众号“思迈科华Smacq”直接联系我们。文章视频内容可点击如下连接跳转：数据采集卡与声音定位

希望您点赞、评论、转发，我们下期再见。

审核编辑 黄宇