反向传播算法的工作原理

反向传播算法（BP算法）是目前用来训练人工神经网络的最常用且最有效的算法。作为谷歌机器学习速成课程的配套材料，谷歌推出一个演示网站，直观地介绍了反向传播算法的工作原理。

反向传播算法对于快速训练大型神经网络来说至关重要。本文将介绍该算法的工作原理。

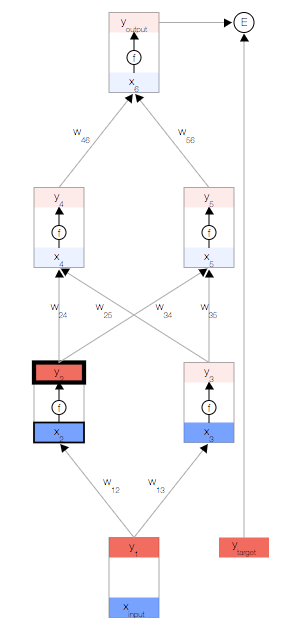
简单的神经网络

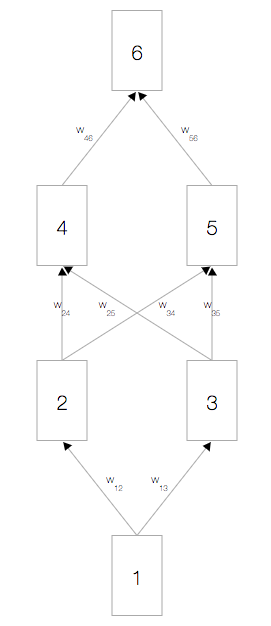
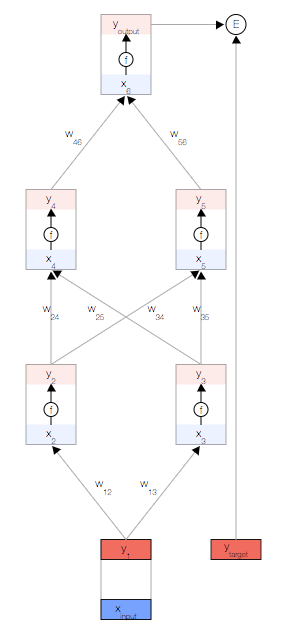
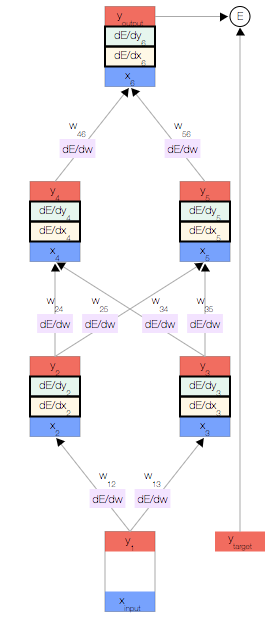
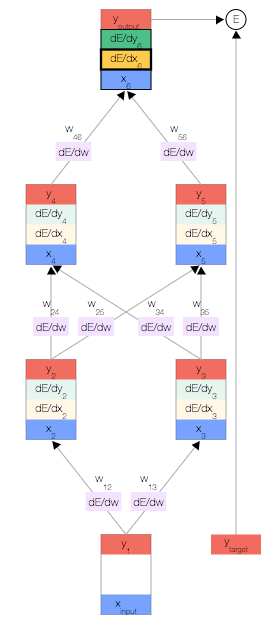
如上图，你会看到一个神经网络，其中包含一个输入节点、一个输出节点，以及两个隐藏层（分别有两个节点）。 

相邻的层中的节点通过权重 相关联，这些权重是网络参数。

激活函数

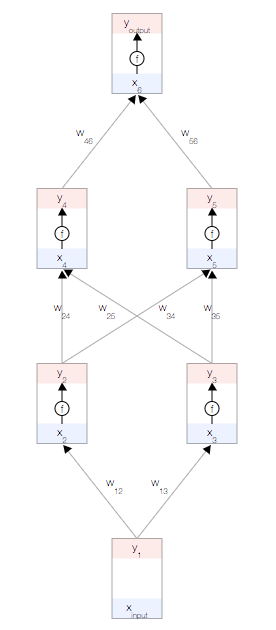
每个节点都有一个总输入 x、一个激活函数 f(x) 以及一个输出 y=f(x)。 

f(x)必须是非线性函数，否则神经网络就只能学习线性模型。 

常用的激活函数是 S 型函数：

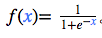
误差函数

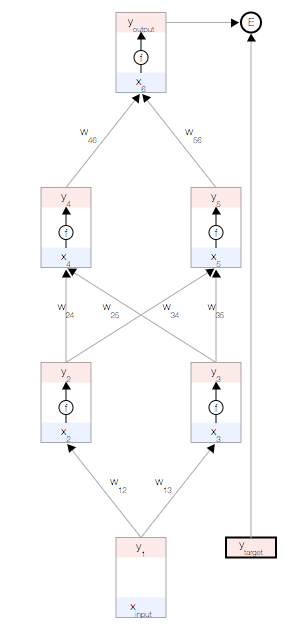
目标是根据数据自动学习网络的权重，以便让所有输入  的预测输出 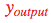接近目标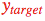 

为了衡量与该目标的差距，我们使用了一个误差函数 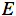常用的误差函数是 

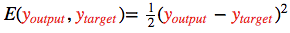
正向传播

首先，我们取一个输入样本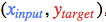并更新网络的输入层。

为了保持一致性，我们将输入视为与其他任何节点相同，但不具有激活函数，以便让其输出与输入相等，即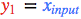 

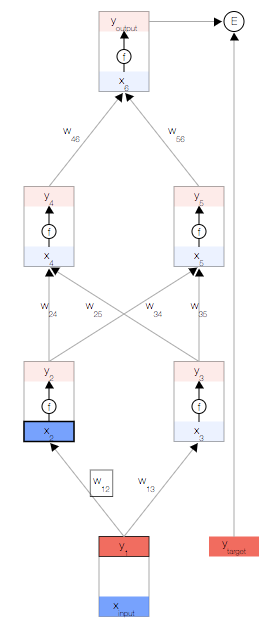
现在，我们更新第一个隐藏层。我们取上一层节点的输出 y，并使用权重来计算下一层节点的输入 x。

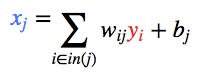
然后，我们更新第一个隐藏层中节点的输出。 为此，我们使用激活函数 f(x)。

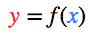
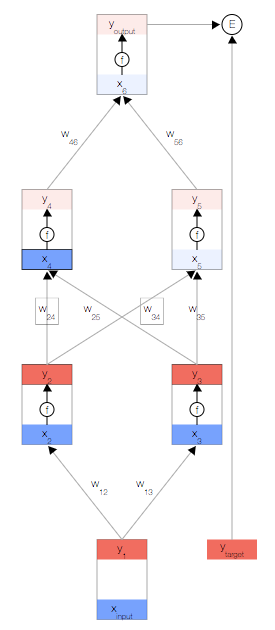
使用这两个公式，我们可以传播到网络的其余内容，并获得网络的最终输出。

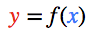
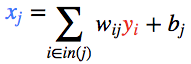
误差导数

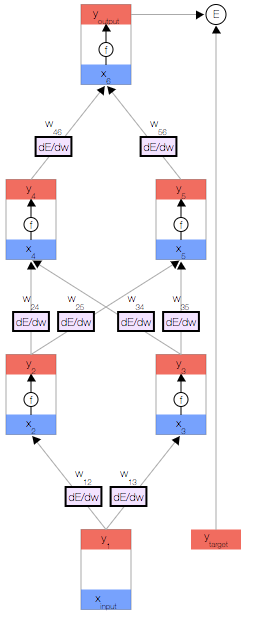
反向传播算法会对特定样本的预测输出和理想输出进行比较，然后确定网络的每个权重的更新幅度。 为此，我们需要计算误差相对于每个权重 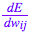的变化情况。

获得误差导数后，我们可以使用一种简单的更新法则来更新权重：

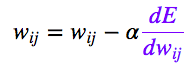
其中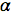，是一个正常量，称为“学习速率”，我们需要根据经验对该常量进行微调。

[注意] 该更新法则非常简单：如果在权重提高后误差降低了 (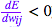)，则提高权重；否则，如果在权重提高后误差也提高了 (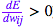)，则降低权重。

其他导数

为了帮助计算 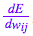，我们还为每个节点分别存储了另外两个导数，即误差随以下两项的变化情况：

反向传播

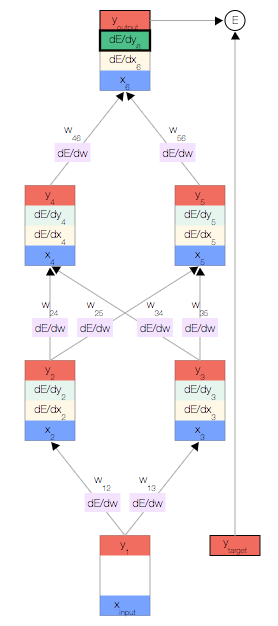
我们开始反向传播误差导数。 由于我们拥有此特定输入样本的预测输出，因此我们可以计算误差随该输出的变化情况。 根据我们的误差函数 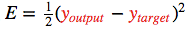，我们可以得出：

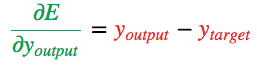
现在我们获得了 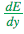，接下来便可以根据链式法则得出 。

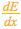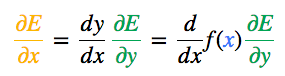
其中，当 f(x) 是 S 型激活函数时，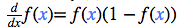

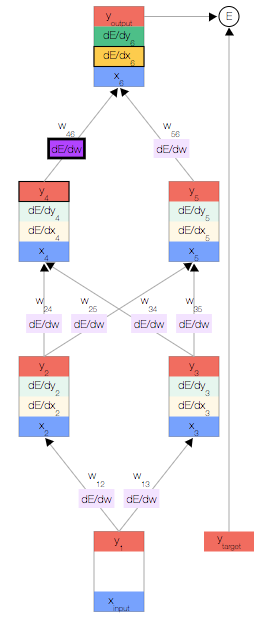
一旦得出相对于某节点的总输入的误差导数，我们便可以得出相对于进入该节点的权重的误差导数。

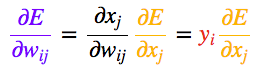
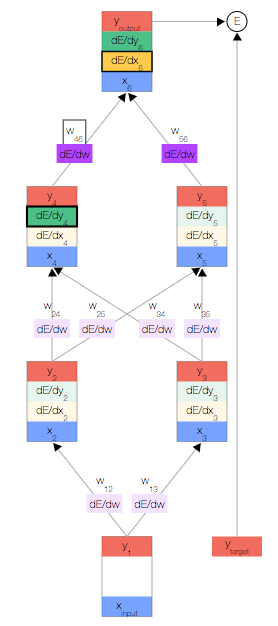
根据链式法则，我们还可以根据上一层得出 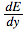。此时，我们形成了一个完整的循环。

接下来，只需重复前面的 3 个公式，直到计算出所有误差导数即可。

结束。