CMU的研究人员Yichong Xu等提出了一种半监督算法排序回归

非参数回归（nonparametric regression）是一种在实践中很有吸引力的方法，因为它非常灵活，对未知回归函数的先验结构假定限制相对宽松。然而，相应的代价是它需要大量标注数据，且随着维度的增加而指数级增长——所谓维度的诅咒（curse of dimensionality）。标注数据极为耗时耗力，而在很多场景下，序信息（ordinal information）的获取则相对而言成本较低。有鉴于此，CMU的研究人员Yichong Xu等提出了一种半监督算法排序回归（Ranking-Regression），结合少量标注样本，加上大量未标注样本的序信息，逃脱维度的诅咒。

非参数方法

在监督学习问题中，我们有一些标注过的数据（观测），然后寻找一个能够较好地拟合这些数据的函数。

给定一些数据点，寻找拟合这些数据点的函数，我们首先想到的就是线性回归：

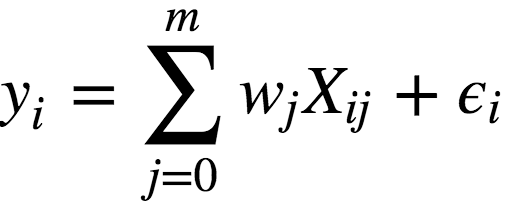
其中：

y为因变量（即目标变量）；

w为模型的参数；

X为观测及其特征矩阵；

ϵ为对应于随机、不可预测的模型错误的变量。

我们可以看到，线性回归的过程，其实就是找出能够最好地拟合观测的参数w，因此，线性回归属于参数方法。

然而，线性回归假定线性模型可以很好地拟合数据，这一假定未必成立。很多数据之间的关系是非线性的，而且很难用线性关系逼近。在这种情况下，我们需要用其他模型才能较好地拟合数据，比如，多项式回归。

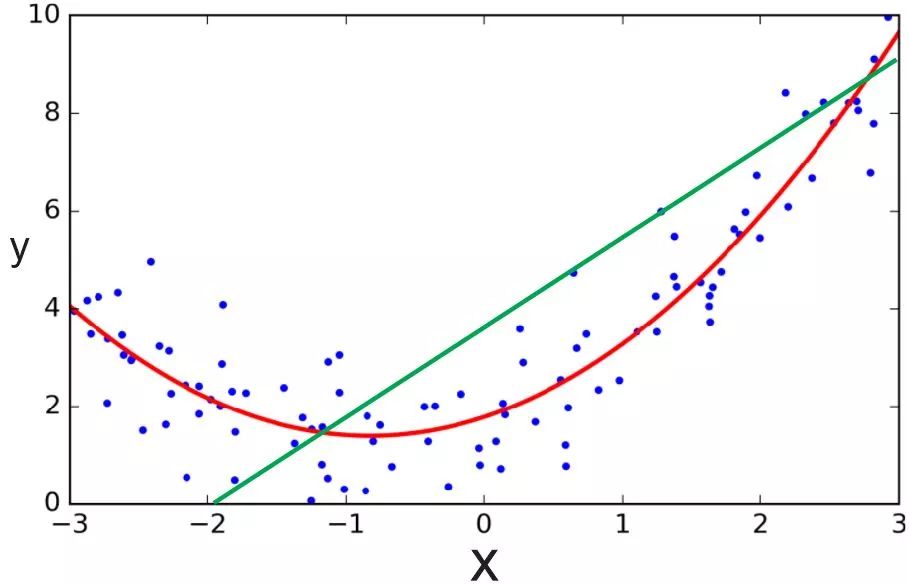
绿线为线性回归，红线为多项式回归；图片来源：ardianumam.wordpress.com

无论是线性回归，还是多项式回归，预先都对模型的结构有比较强的假定，例如数据可以通过线性函数或多项式函数来拟合，而这些假定不一定成立。因此，许多场景下，我们需要使用非参数回归，也就是说，我们不仅需要找到回归函数的参数，还需要找到回归函数的结构。

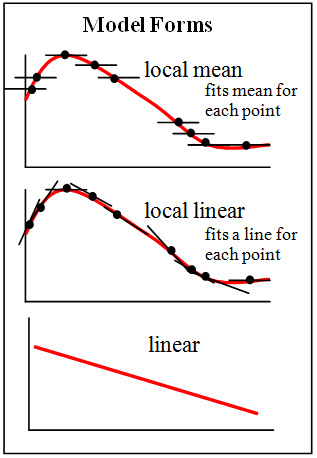
图片来源：Brmccune；许可： CC BY-SA 3.0

例如，通常用于分类的K近邻算法，其实还可以用于回归。用于回归的K近邻算法，其基本流程和一般的用于分类的K近邻算法差不多，唯一的区别是，分类时，目标变量的分类为它的最近邻中最常见的分类（众数），而回归时，目标变量的值为它的最近邻的均值（或中位数）。用于回归的K近邻算法，就是一种非参数回归方法。

当然，非参数方法的灵活性不是没有代价的。由于不仅回归函数的参数未知，回归函数的结构也未知，相比参数方法，我们需要更多的标注数据来训练，以得到较好的结果。而随着维度的增加，我们需要的标注数据的数量呈指数级增长。这也正是我们前面提到的维度的诅咒。前面我们举了K近邻作为非线性回归的例子，而K近邻正因受维度诅咒限制而出名。

有鉴于此，许多研究致力于通过给非参数回归增加结构上的限制来缓解这一问题，例如，稀疏性或流形的限制（很多时候，高维数据空间是稀疏的，有时高维数据甚至基本上处于一个低维流形之上）。这是一件很有意思的事情。在实践中，之所以选用非参数回归，正是看重其灵活性，对拟合函数的结构没有很强的假定。然而，当非参数回归遇到维度诅咒的时候，我们又退回一步，通过加强结构上的假定来缓解维度诅咒问题。

而CMU的研究人员Yichong Xu、Hariank Muthakana、Sivaraman Balakrishnan、Aarti Singh、 Artur Dubrawski则采用了另外的做法，使用具有序信息的较大数据集补充带标注的较小数据集，缓解非参数回归在高维度下的问题。这一做法在实践中意义很大，因为相对标签而言，序信息的收集成本要低很多。例如，在临床上，精确地评估单个患者的健康状况可能比较困难，但是比较两个患者谁更健康，则比较容易，也比较精确。

排序回归算法

研究人员提出的排序回归（Ranking-Regression）算法（以下简称R2），其基本直觉是根据序信息推断未标注数据点的值。具体而言，根据序信息排序数据点，之后应用保序回归（isotonic regression），然后根据已标注数据点和序信息推断未标注数据点的值。经过以上过程之后，就可以用最近邻算法估计新数据点的值了。

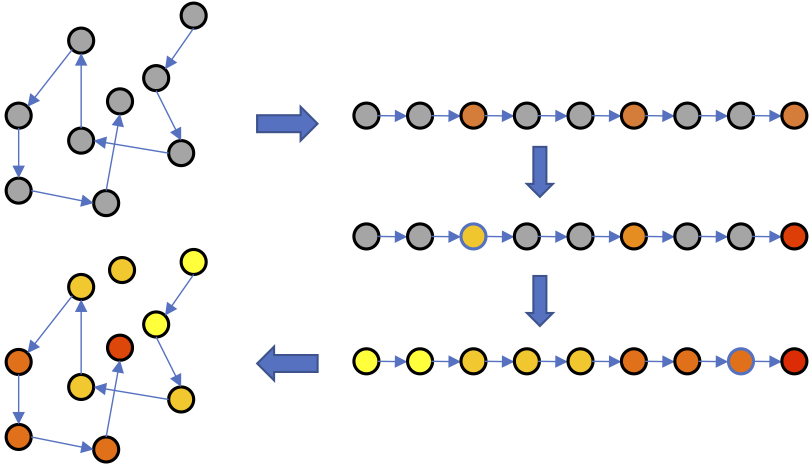
算法示意图

上为R2算法示意图。当然，如果你更习惯看伪代码的话：

R2的上下界

显然，用序信息代替标签，有以次充好之嫌。因此，研究人员研究了R2算法的误差上下界。

正如之前提到的，非参数回归对结构的假定比较宽松，但也并不是毫无限制的。研究人员采用了经典的非参数回归限制：

未标签数据集{X1, ..., Xn}中，Xi ∈ X ⊂ [0,1]d，且Xi均匀独立抽取自分布Px。而Px满足其密度p(x)对x ∈ [0,1]d而言是有界的，即 0 < pmin <= p(x) <= pmax。

回归函数f同样也是有界的（[-M, M]），并且是赫尔德连续的，在0 < s <= 1时，

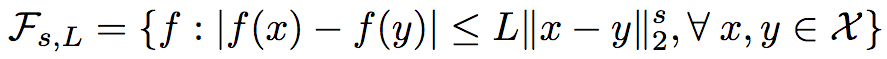
在满足以上条件的条件下，研究人员证明了R2得出的回归函数的均方误差上界为：

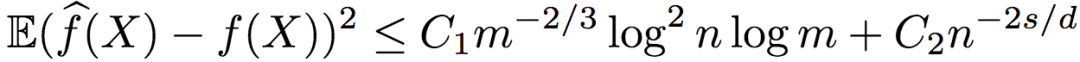
其中，C1、C2为大于0的常数。

而回归函数的均方误差下界为：

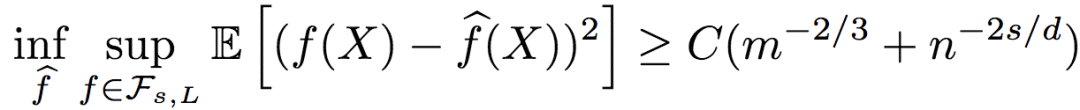
其中，C为大于0的常数。

由误差上下界可知，基于序信息的排序回归效果不错，从对数因子上来说是最优的。

另外，从R2误差的上界来看，只有序信息（n）依赖于维度d（不等式右侧第二项），而标注信息并不依赖维度d（不等式右侧第一项），也就是说，R2逃脱了维度的诅咒。

限于篇幅，这里就不介绍了证明过程了。上下界的证明思路，分别见论文的3.1小节和3.2小节；详细证明过程，分别见论文的附录B、C。

含噪声的序信息

虽然之前说过序信息相对容易取得，也比较容易保持精确，但实际数据难免会有噪声——错误的序信息。之前的结论都是在序信息不含噪声的前提下得出的，那么，当序信息有噪声的时候，情况又是怎么样的呢？

研究人员进一步推导了序信息包含噪声的情况。当然，噪声是控制在一定范围之内的。假定根据含噪序信息所得到的排序与真实排序之间的Kendall-Tau距离不超过vn2（n代表只有序信息的未标注数据），则R2的均方误差的上界为：

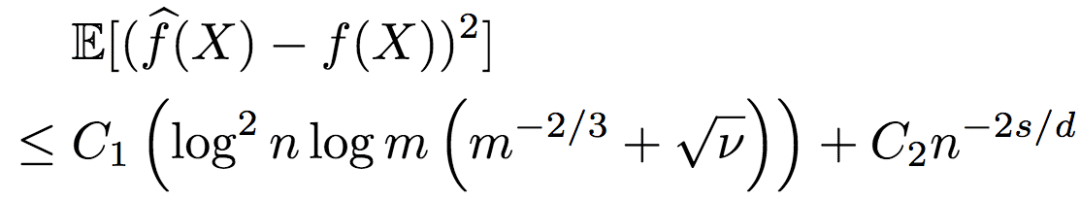
下界为：

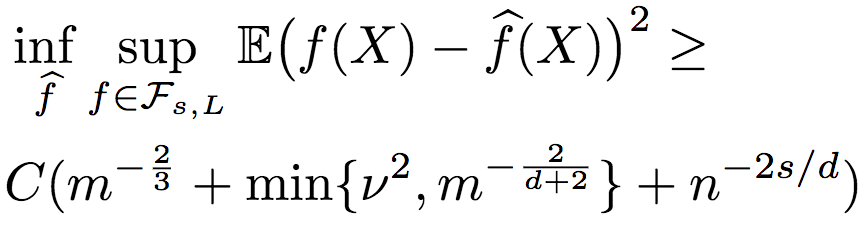
由此可知，R2的鲁棒性相当好。当有足够的序信息时，即使序信息包含一些噪声，标注数据仍然不依赖于维度，也就是说，R2仍能逃脱维度的诅咒。

同样，我们这里不给出具体的证明过程。请参考论文4.1、4.2小节了解证明思路，论文附录D、F了解详细证明过程。

另外，研究人员还进一步证明了（证明过程见附录E），存在逼近函数f满足

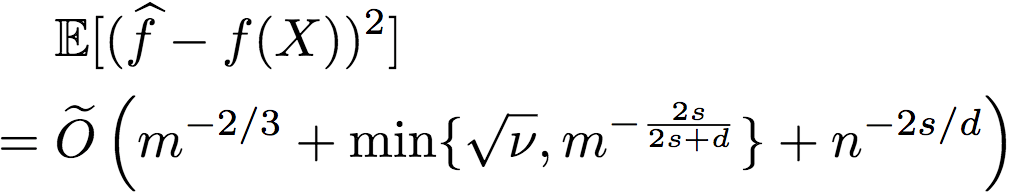
这就意味着，当噪声过大（v过大）时，通过使用交叉验证过程（R2和忽略序信息的简单非参数回归器），我们可以选择较好的回归方法，从而取得较优的表现。事实上，当我们有足够标签时，即使序信息非常噪杂，以上比率仍能收敛至0.

含噪声的成对比较

有的时候，序信息是以成对比较（pairwise comparison）（数据点两两之间的大小）的形式取得的。当不含噪声的时候，成对比较和之前提到的标准排序形式是等价的。但有噪声的情况却有所不同。研究人员证明了，在序信息为含噪声的成对比较时，逼近函数的均方误差的上界为：

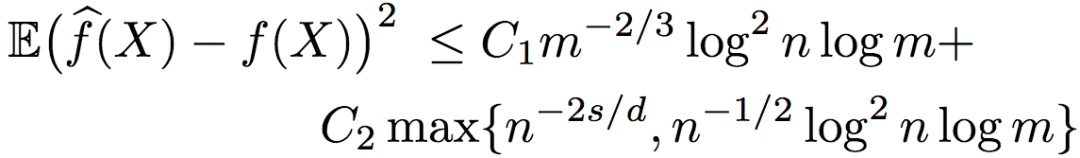
其中，C1和C2为大于0的常数。

由上式可知，当维度d >= 4s时，误差取决于n-2s/d，并且，在这一设定下，基于含噪声的成对比较的排序回归，同样从对数因子上来说是最优的。

试验

为了验证理论结果以及测试R2的实际表现，研究人员进行了一些试验：

在模拟数据上进行试验，这样可以充分控制噪声

在UCI数据集上进行试验，通过标签模拟排序

试验R2在实际应用中的表现

在所有试验中，研究人员对比了R2和K近邻算法的表现。之所以选择K近邻，是因为K近邻在理论上接近最优，并在实践中应用广泛。理论上说，有m个标注样本时，k的最优值为m2/(d+2)。然而，对研究人员考虑的所有m、d值而言，m2/(d+2)非常小（< 5）。因此，研究人员的试验中选用的是一组常量k值（不随m改变）。每个试验重复了20次，并对均方误差取平均值。

模拟数据

研究人员采用如下方法生成了数据：令d = 8，均匀取样X自[0, 1]d。目标函数为：

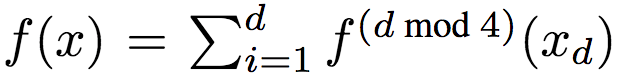
其中，xd为x的第d维，且

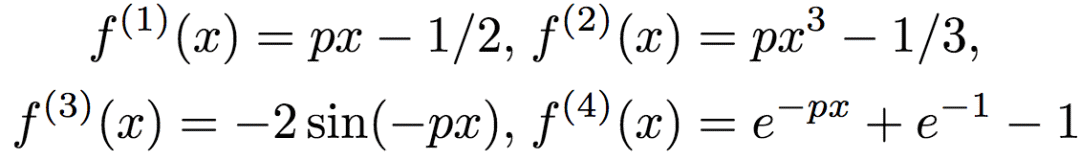
其中，p随机均匀取样自[0, 10]。研究人员调整了f(x)，使其均值为0，方差为单位方差。通过y = f(x) + ε，ε ~ N(0, 0.52)生成标签。

研究人员为训练集和测试集各生成了1000个样本。

研究人员测试了R2的两个变体，1-NN和5-NN，在算法的最后一步分别使用1、5个最近邻。5-NN并不影响之前理论分析部分的上下界，然而，从经验出发，研究人员发现5-NN提升了表现。

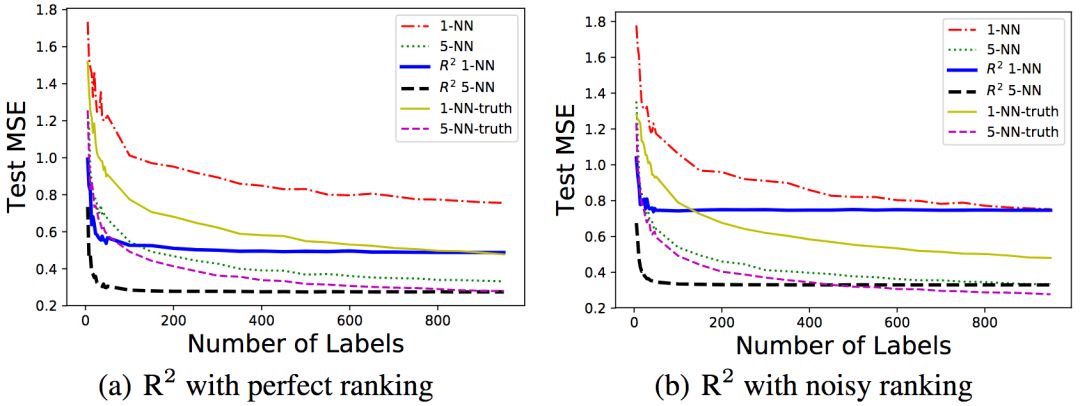
左：序信息无噪声；右：序信息有噪声

从上图可以看到，无论序信息是否有噪声，R2的表现都很好。

为了研究序信息噪声的影响，研究人员在固定标注/排序样本数100/1000的情况下，改变了序信息噪声的等级。对噪声水平σ，序信息通过y' = f(x) + ε'生成，其中ε' ~ N(0, σ2)。

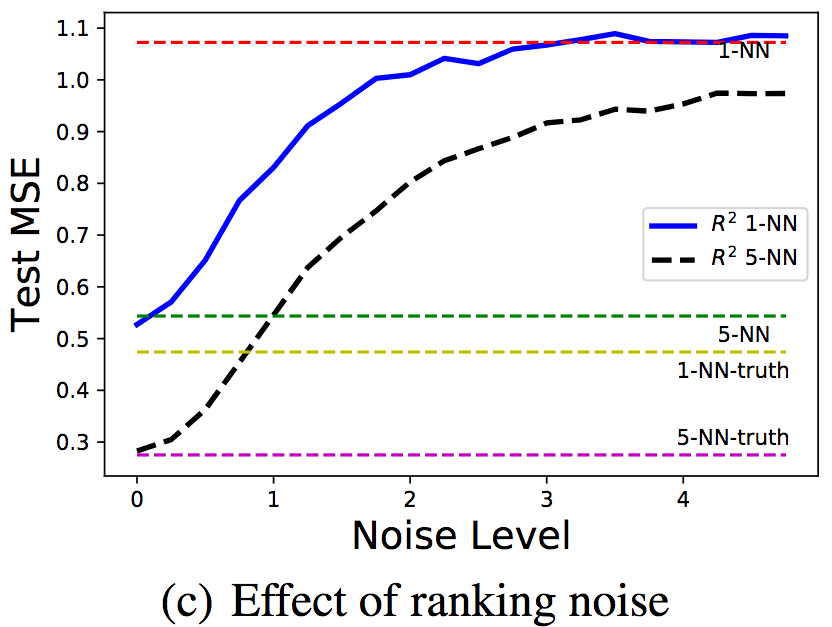
可以看到，随着噪声水平的升高，均方误差也相应升高了。

UCI数据集

研究人员在两个UCI回归数据集上进行了试验。这两个数据集分别为Boston-Housing（波士顿房价）和diabetes（糖尿病）。序信息是通过数据集标签生成的。

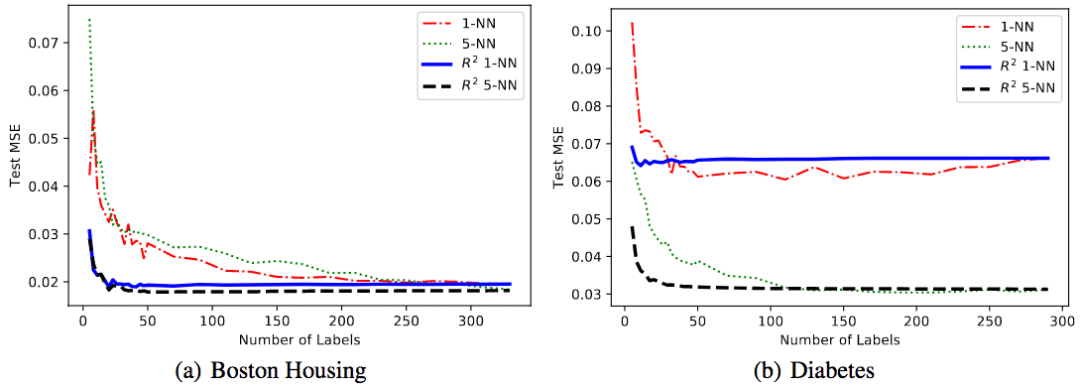
可以看到，相比不使用序信息的基线，R2在两个数据集上的表现都更好。

根据肖像预测年龄

为了进一步在实践中验证R2算法，研究人员考虑了根据肖像估计人员年龄的任务。

研究人员使用了APPA-REAL数据集，该数据集包含7591张图像，每张图像都有相应的生物学年龄和表观年龄。生物学年龄为实际年龄，表观年龄基于众包收集。根据多人的估计的平均值得到表观年龄（平均有38个不同的估计者）。APPA-REAL同时提供了表观年龄估计的标准差。数据集分为三部分，4113张训练图像、1500张验证图像、1978张测试图像，研究人员的试验只使用了训练和验证样本。

研究人员使用FaceNet的最后一层从每张图像中提取了128个维度的特征，并缩放每项特征使每个样本X ∈ [0, 1]d。研究人员使用了5-NN和10-NN。除了像之前的试验一样，使用不包含序信息的5-NN、10-NN作为基线外，还比较了核支持向量回归（SVR）的表现。SVR的参数配置为scikit-learn的标准配置，惩罚参数C = 1，RBF核，tolerance值为0.1.

研究人员试验了两个任务：

第一个任务的目标是预测生物学年龄。标签为生物学年龄，而序信息基于表观年龄生成。这是为了模拟现实场景，有一小部分样本的真实年龄信息，但希望通过众包的方式收集更多样本的年龄信息。而在众包时，让人对样本的长幼进行排序，要比直接估计年龄要容易一点，也精确一点。

第二个任务的目标是预测表观年龄。在这一任务中，标签和排序根据APPA-REAL提供的标准差生成。具体而言，标签取样自一个高斯分布，其均值等于表观年龄，标准差为数据集提供的标准差。排序的生成分两步，首先根据同样的分布生成标签，然后根据标签排序。这是为了模拟现实场景中，让人同时估计样本的年龄，并对样本的长幼进行排序。注意，在真实应用中，相比试验，排序的噪声会低一点。

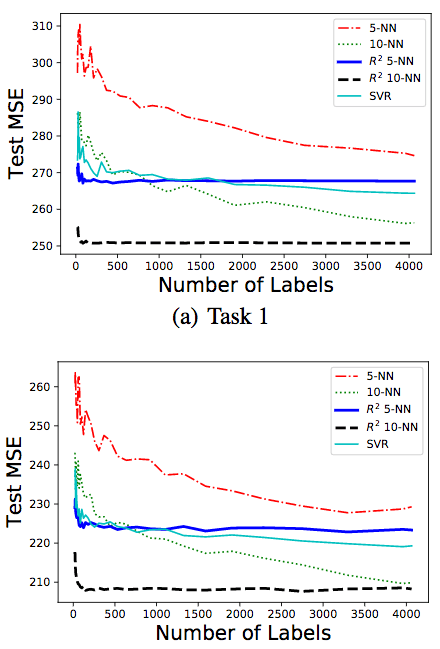
结果如上图所示。我们可以看到，10-NN版本的R2的表现最好。而当样本数少于500时，R2的10-NN版本和5-NN版本均优于其他算法。

结语

论文可通过预印本文库获取：arXiv:1806.03286

另外，本文作者将在ICML 2018上做口头报告（Wed Jul 11th 11:00 -- 11:20 AM @ A6）。