

经典的采样方法有哪些?
电子说
描述
▌引子
最近开始拾起来看一些 NLP 相关的东西,特别是深度学习在 NLP 上的应用,发现采样方法在很多模型中应用得很多,因为训练的时候如果预测目标是一个词,直接的 softmax 计算量会根据单词数量的增长而增长。恰好想到最开始深度学习在 DBN 的时候采样也发挥了关键的作用,而自己对采样相关的方法了解不算太多,所以去学习记录一下,经典的统计的方法确实巧妙,看起来非常有收获。
本篇文章先主要介绍一下经典的采样方法如 Inverse Sampling、Rejective Sampling 以及 Importance Sampling 和它在 NLP 上的应用,后面还会有一篇来尝试介绍 MCMC 这一组狂炫酷拽的算法。才疏学浅,行文若有误望指正。
▌Why Sampling
采样是生活和机器学习算法中都会经常用到的技术,一般来说采样的目的是评估一个函数在某个分布上的期望值,也就是
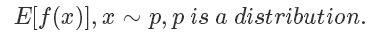
比如我们都学过的抛硬币,期望它的结果是符合一个伯努利分布的,定义正面的概率为 p ,反面概率为 1-p 。最简单地使 f(x)=x,在现实中我们就会通过不断地进行抛硬币这个动作,来评估这个概率p。
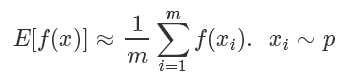
这个方法也叫做蒙特卡洛法(Monte Carlo Method),常用于计算一些非常复杂无法直接求解的函数期望。
对于抛硬币这个例子来说:
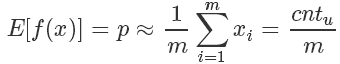
其期望就是抛到正面的计数 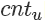 除以总次数 m。
除以总次数 m。
而我们抛硬币的这个过程其实就是采样,如果要用程序模拟上面这个过程也很简单,因为伯努利分布的样本很容易生成:
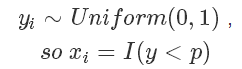
而在计算机中的随机函数一般就是生成 0 到 1 的均匀分布随机数。
▌Sampling Method
可以看到蒙特卡洛法其实就是按一定的概率分布中获取大量样本,用于计算函数在样本的概率分布上的期望。其中最关键的一个步骤就是如何按照指定的概率分布 p 进行样本采样,抛硬币这个 case 里伯努利分布是一个离散的概率分布,它的概率分布一般用概率质量函数(pmf)表示,相对来说比较简单,而对于连续概率分布我们需要考虑它的概率密度函数(pdf):
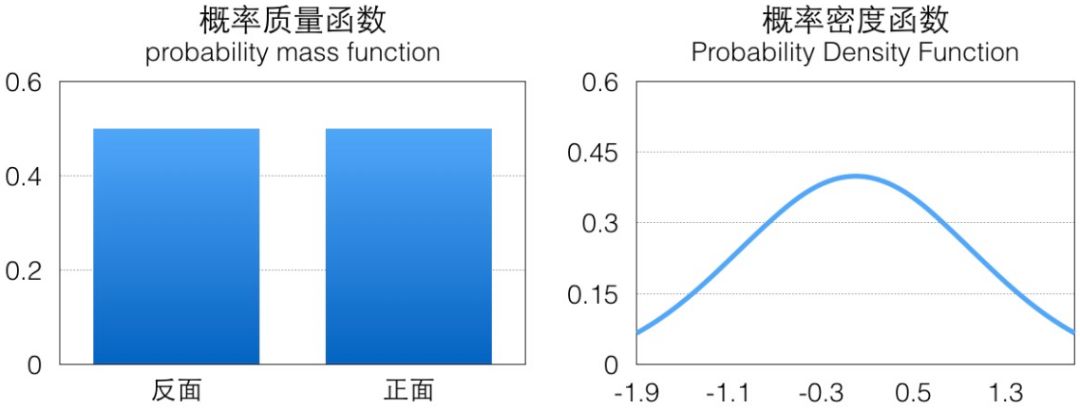
比如上图示例分别是标准正态分布概率密度函数,它们的面积都是 1(这是概率的定义),如果我们可以按照相应概率分布生成很多样本,那这些样本绘制出来的直方图应该跟概率密度函数是一致的。
而在实际的问题中,p 的概率密度函数可能会比较复杂,我们由浅入深,看看如何采样方法如何获得服从指定概率分布的样本。
▌Inverse Sampling
对于一些特殊的概率分布函数,比如指数分布:
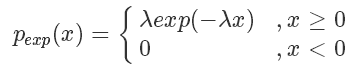
我们可以定义它的概率累积函数(Cumulative distribution function),也就是(ps.这个’F’和前面的’f’函数并没有关系)
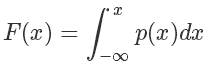
从图像上看就是概率密度函数小于 x 部分的面积。这个函数在 x≥0 的部分是一个单调递增的函数(在定义域上单调非减),定义域和值域是[0,+∞)→[0,1),画出来大概是这样子的一个函数,在 p(x) 大的地方它增长快(梯度大),反之亦然:
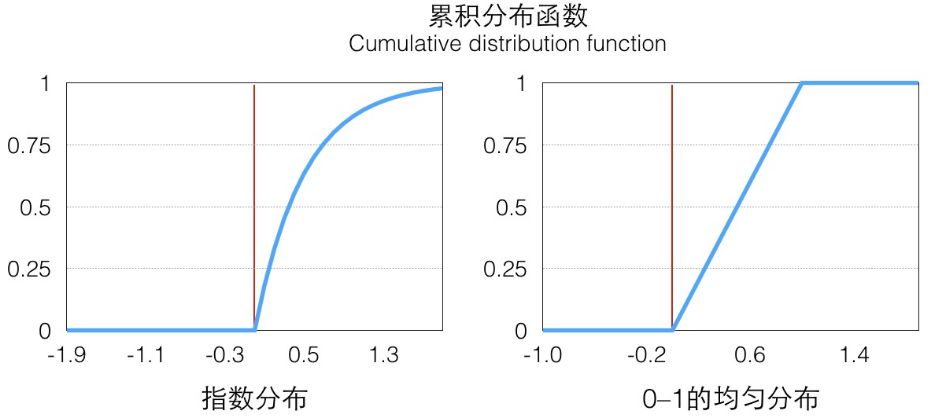
因为它是唯一映射的(在>0的部分,接下来我们只考虑这一部分),所以它的反函数可以表示为 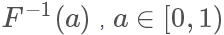 ,值域为[0,+∞)
,值域为[0,+∞)
因为F单调递增,所以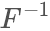 也是单调递增的:
也是单调递增的:
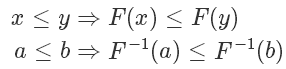
利用反函数的定义,我们有:
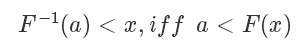
我们定义一下 [0,1] 均匀分布的 CDF,这个很好理解:
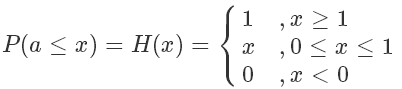
所以
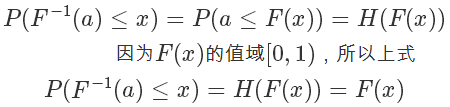
根据 F(x) 的定义,它是 exp 分布的概率累积函数,所以上面这个公式的意思是 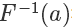 符合 exp 分布,我们通过 F 的反函数将一个 0 到 1 均匀分布的随机数转换成了符合 exp 分布的随机数,注意,以上推导对于 cdf 可逆的分布都是一样的,对于 exp 来说,它的反函数的形式是:
符合 exp 分布,我们通过 F 的反函数将一个 0 到 1 均匀分布的随机数转换成了符合 exp 分布的随机数,注意,以上推导对于 cdf 可逆的分布都是一样的,对于 exp 来说,它的反函数的形式是:
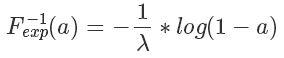
具体的映射关系可以看下图(a),我们从 y 轴 0-1 的均匀分布样本(绿色)映射得到了服从指数分布的样本(红色)。
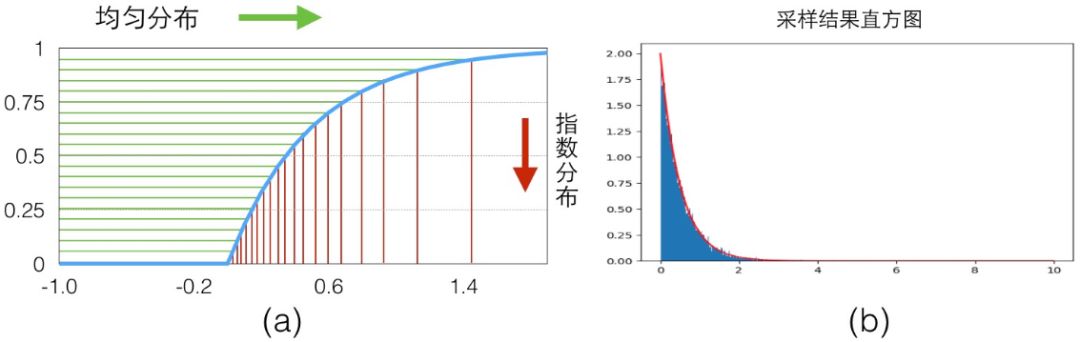
我们写一点代码来看看效果,最后绘制出来的直方图可以看出来就是 exp 分布的图,见上图(b),可以看到随着采样数量的变多,概率直方图和真实的 CDF 就越接近:
def sampleExp(Lambda = 2,maxCnt = 50000): ys = [] standardXaxis = [] standardExp = [] for i in range(maxCnt): u = np.random.random() y = -1/Lambda*np.log(1-u) #F-1(X) ys.append(y) for i in range(1000): t = Lambda * np.exp(-Lambda*i/100) standardXaxis.append(i/100) standardExp.append(t) plt.plot(standardXaxis,standardExp,'r') plt.hist(ys,1000,normed=True) plt.show()
▌Rejective Sampling
我们在学习随机模拟的时候通常会讲到用采样的方法来计算 π 值,也就是在一个 1×1 的范围内随机采样一个点,如果它到原点的距离小于 1,则说明它在1/4 圆内,则接受它,最后通过接受的占比来计算 1/4 圆形的面积,从而根据公式反算出预估的ππ值,随着采样点的增多,最后的结果 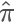 会越精准。
会越精准。

上面这个例子里说明一个问题,我们想求一个空间里均匀分布的集合面积,可以尝试在更大范围内按照均匀分布随机采样,如果采样点在集合中,则接受,否则拒绝。最后的接受概率就是集合在‘更大范围’的面积占比。
当我们重新回过头来看想要 sample 出来的样本服从某一个分布 p,其实就是希望样本在其概率密度函数 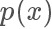 高的地方出现得更多,所以一个直觉的想法,我们从均匀分布随机生成一个样本
高的地方出现得更多,所以一个直觉的想法,我们从均匀分布随机生成一个样本 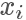 ,按照一个正比于
,按照一个正比于 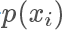 的概率接受这个样本,也就是说虽然是从均匀分布随机采样,但留下的样本更有可能是
的概率接受这个样本,也就是说虽然是从均匀分布随机采样,但留下的样本更有可能是 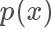 高的样本。
高的样本。
这样的思路很自然,但是否是对的呢。其实这就是 Rejective Sampling 的基本思想,我们先看一个很 intuitive 的图
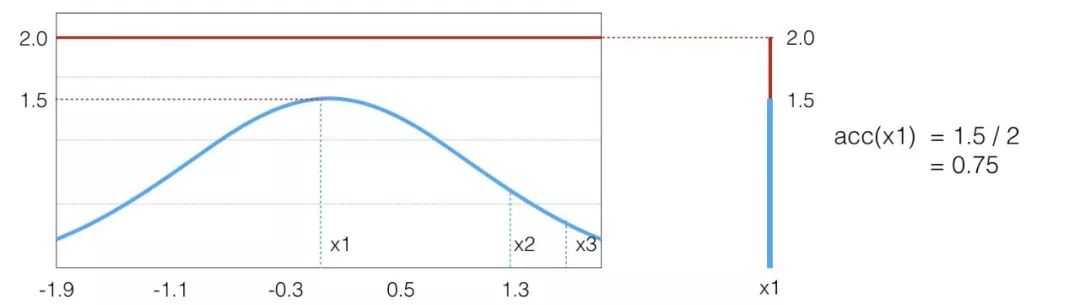
假设目标分布的 pdf 最高点是 1.5,有三个点它们的 pdf 值分别是
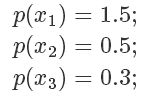
因为我们从 x 轴上是按均匀分布随机采样的,所以采样到三个点的概率都一样,也就是
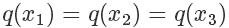
接下来需要决定每个点的接受概率 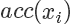 ,它应该正比于
,它应该正比于 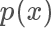 ,当然因为是概率值也需要小于等于 1.
,当然因为是概率值也需要小于等于 1.
我们可以画一根 y=2 的直线,因为整个概率密度函数都在这根直线下,我们设定
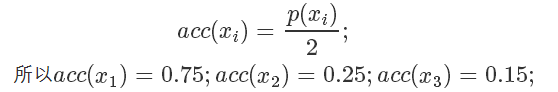
我们要做的就是生成一个 0-1的随机数 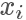 ,如果它小于接受概率
,如果它小于接受概率 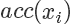 ,则留下这个样本。因为
,则留下这个样本。因为 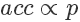 ,所以可以看到因为
,所以可以看到因为 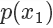 是
是 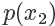 的3倍,所以
的3倍,所以 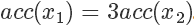 。同样采集 100 次,最后留下来的样本数期望也是 3 倍。这根本就是概率分布的定义!
。同样采集 100 次,最后留下来的样本数期望也是 3 倍。这根本就是概率分布的定义!
我们将这个过程更加形式化一点,我们我们又需要采样的概率密度函数
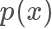 ,但实际情况我们很有可能只能计算出
,但实际情况我们很有可能只能计算出 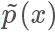 ,有
,有
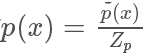
我们需要找一个可以很方便进行采样的分布函数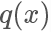 并使
并使
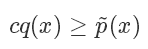
其中 c 是需要选择的一个常数。然后我们从 q 分布中随机采样一个样本 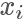 ,并以
,并以
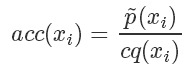
的概率决定是否接受这个样本。重复这个过程就是「拒绝采样」算法了。
在上面的例子我们选择的 q 分布是均匀分布,所以从图像上看其 pdf 是直线,但实际上 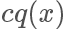 和
和 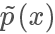 越接近,采样效率越高,因为其接受概率也越高:
越接近,采样效率越高,因为其接受概率也越高:
▌Importance Sampling
上面描述了两种从另一个分布获取指定分布的采样样本的算法,对于1.在实际工作中,一般来说我们需要 sample 的分布都及其复杂,不太可能求解出它的反函数,但 p(x) 的值也许还是可以计算的。对于2.找到一个合适的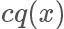
那我们回过头来看我们sample的目的:其实是想求得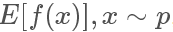 ,也就是
,也就是
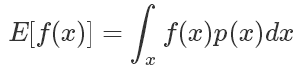
如果符合 p(x) 分布的样本不太好生成,我们可以引入另一个分布 q(x),可以很方便地生成样本。使得
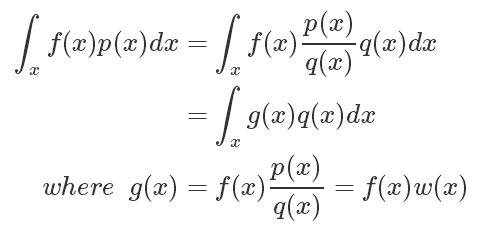
我们将问题转化为了求 g(x) 在 q(x) 分布下的期望!!!
我们称其中的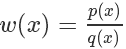 叫做 Importance Weight.
叫做 Importance Weight.
▌Importance Sample 解决的问题
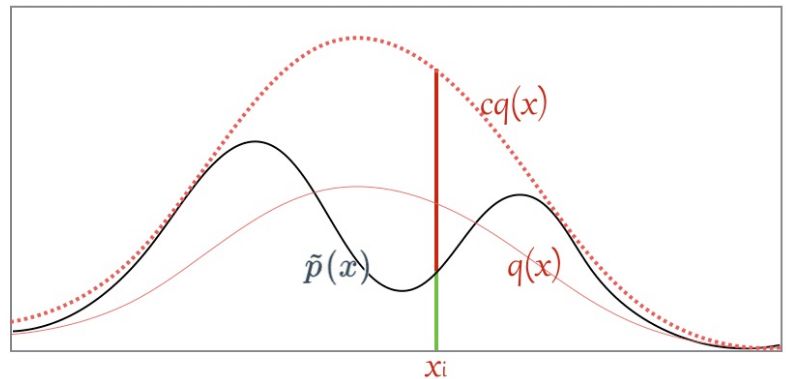
首先当然是我们本来没办法 sample from p,这个是我们看到的,IS 将之转化为了从 q 分布进行采样;同时 IS 有时候还可以改进原来的 sample,比如说:
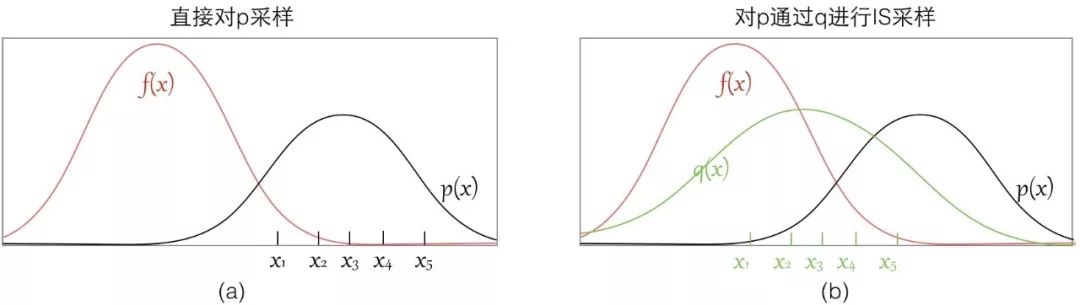
可以看到如果我们直接从 p 进行采样,而实际上这些样本对应的 f(x) 都很小,采样数量有限的情况下很有可能都无法获得 f(x) 值较大的样本,这样评估出来的期望偏差会较大;
而如果我们找到一个 q 分布,使得它能在 f(x)*p(x) 较大的地方采集到样本,则能更好地逼近 [Ef(x)],因为有 Importance Weight 控制其比重,所以也不会导致结果出现过大偏差。
所以选择一个好的p也能帮助你sample出来的效率更高,要使得 f(x)p(x)较大的地方能被 sample出来。
▌无法直接求得p(x)的情况
上面我们假设 g(x) 和 q(x) 都可以比较方便地计算,但有些时候我们这个其实是很困难的,更常见的情况市我们能够比较方便地计算 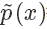 和
和 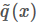
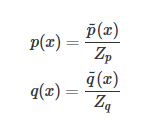
其中 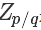 是一个标准化项(常数),使得
是一个标准化项(常数),使得 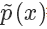 或者
或者 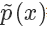 等比例变化为一个概率分布,你可以理解为 softmax 里面那个除数。也就是说
等比例变化为一个概率分布,你可以理解为 softmax 里面那个除数。也就是说
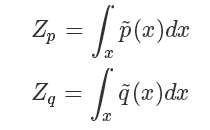
这种情况下我们的 importance sampling 是否还能应用呢?
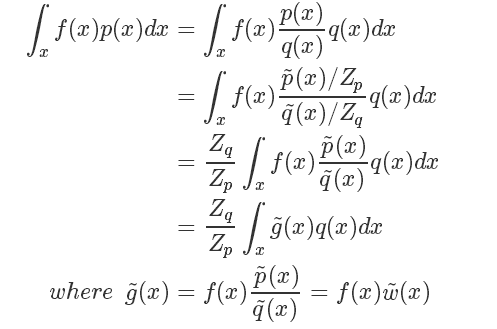
而 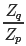 我们直接计算并不太好计算,而它的倒数:
我们直接计算并不太好计算,而它的倒数:
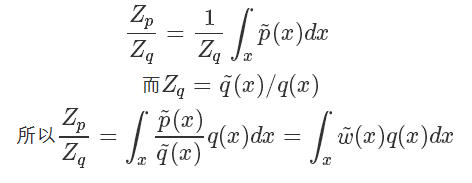
因为我们家设能很方便地从 q 采样,所以上式其实又被转化成了一个蒙特卡洛可解的问题,也就是
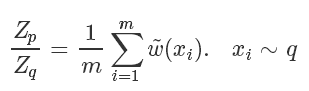
最终最终,原来的蒙特卡洛问题变成了:
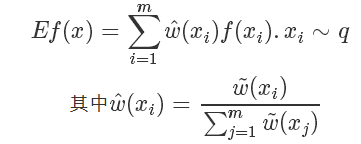
所以我们完全不用知道 q(x) 确切的计算值,就可以近似地从中得到在 q 分布下 f(x) 的取值!!amazing!
▌Importance Sampling在深度学习里面的应用
在深度学习特别是NLP的Language Model中,训练的时候最后一层往往会使用 softmax 函数并计算相应的梯度。
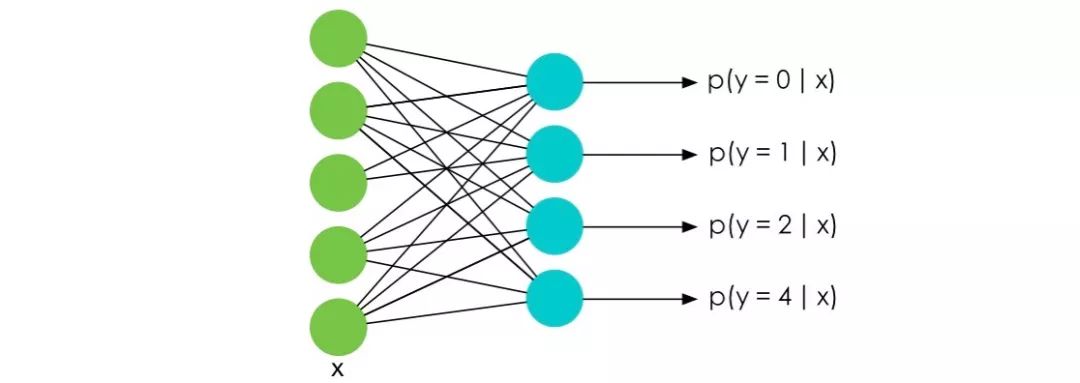
而我们知道 softmax 函数的表达式是:
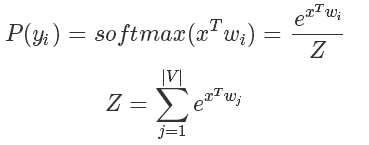
要知道在 LM 中 m 的大小是词汇的数量决定的,在一些巨大的模型里可能有几十万个词,也就意味着计算Z的代价十分巨大。
而我们在训练的时候无非是想对 softmax 的结果进行求导,也就是说
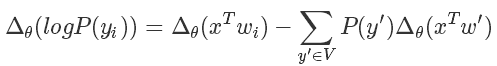
后面那一块,我们好像看到了熟悉的东西,没错这个形式就是为采样量身定做似的。
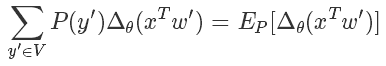
经典的蒙特卡洛方法就可以派上用途了,与其枚举所有的词,我们只需要从 V 里 sample 出一些样本词,就可以近似地逼近结果了。
同时直接从 P 中 sample 也不可取的,而且计算 P是非常耗时的事情(因为需要计算Z),我们一般只能计算 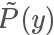 ,而且直接从 P 中 sample 也不可取,所以我们选择另一个分布 Q 进行 Importance Sample 即可。
,而且直接从 P 中 sample 也不可取,所以我们选择另一个分布 Q 进行 Importance Sample 即可。
一般来说可能选择的 Q 分布是简单一些的 n-gramn 模型。下面是论文中的算法伪代码,基本上是比较标准的流程(论文图片的符号和上面的描述稍有出入,理解一下过程即可):

References
【1】mathematicalmonk’s machine learning course on y2b. machine learing
【2】Pattern Recognition And Machine Learning
【3】Adaptive Importance Sampling to Accelerate Training of a Neural Probabilistic Language Model.Yoshua Bengio and Jean-Sébastien Senécal.
采样方法 2
▌引子
在上面我们讲到了拒绝采样、重要性采样一系列的蒙特卡洛采样方法,但这些方法在高维空间时都会遇到一些问题,因为很难找到非常合适的可采样Q分布,同时保证采样效率以及精准度。
本文将会介绍采样方法中最重要的一族算法,MCMC(Markov Chain Monte Carlo),在之前我们的蒙特卡洛模拟都是按照如下公式进行的:
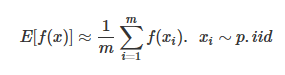
我们的x都是独立采样出来的,而在MCMC中,它变成了
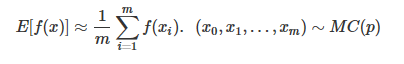
其中的MC(p)就是我们本文的主角之一,马尔可夫过程(Markov Process)生成的马尔可夫链(Markov Chain)。
▌Markov Chain(马尔可夫链)
在序列的算法(一·a)马尔可夫模型中(https://blog.csdn.net/dark_scope/article/details/61417336)我们就说到了马尔可夫模型的马尔可夫链,简单来说就是满足马尔可夫假设
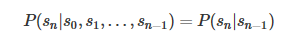
的状态序列,由马尔可夫过程(Markov Process)生成。
一个马尔可夫过程由两部分组成,一是状态集合 Ω,二是转移概率矩阵 T。
其流程是:选择一个初始的状态分布 π0,然后进行状态的转移:
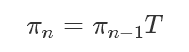
得到的 π0,π1,π2 ...πn 状态分布序列。
注意:我们在这里讲的理论和推导都是基于离散变量的,但其实是可以直接推广到连续变量。
马尔可夫链在很多场景都有应用,比如大名鼎鼎的 pagerank 算法,都用到了类似的转移过程;
马尔可夫链在某种特定情况下,有一个奇妙的性质:在某种条件下,当你从一个分布 π0 开始进行概率转移,无论你一开始 π0 的选择是什么,最终会收敛到一个固定的分布 π,叫做稳态(steady-state)。
稳态满足条件:
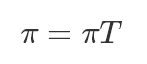
这里可以参考《LDA数学八卦0.4.2》的例子,非常生动地描述了社会阶层转化的一个例子,也对MCMC作了非常好的讲解
书归正传,回到我们采样的场景,我们知道,采样的难点就在于概率密度函数过于复杂而无法进行有效采样,如果我们可以设计一个马尔可夫过程,使得它最终收敛的分布是我们想要采样的概率分布,不就可以解决我们的问题了么。
前面提到了在某种特定情况下,这就是所有MCMC算法的理论基础 Ergodic Theorem:
如果一个离散马尔可夫链 (x0,x1...xm)是一个与时间无关的 Irreducible 的离散,并且有一个稳态分布 π,则:

它需要满足的条件有这样几个,我们直接列在这里,不作证明:
1.Time homogeneous: 状态转移与时间无关,这个很好理解。 2.Stationary Distribution: 最终是会收敛到稳定状态的。 3.Irreducible: 任意两个状态之间都是可以互相到达的。 4.Aperiodic:马尔可夫序列是非周期的,我们所见的绝大多数序列都是非周期的。
虽然这里要求是离散的马尔可夫链,但实际上对于连续的场景也是适用的,只是转移概率矩阵变成了转移概率函数。
▌MCMC
在上面马尔可夫链中我们的所说的状态都是某个可选的变量值,比如社会等级上、中、下,而在采样的场景中,特别是多元概率分布,并不是量从某个维度转移到另一个维度,比如一个二元分布,二维平面上的每一个点都是一个状态,所有状态的概率和为 1! 这里比较容易产生混淆,一定小心。
在这里我们再介绍一个概念:
Detail balance:一个马尔可夫过程是细致平稳的,即对任意 a,b 两个状态:
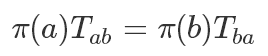
细致平稳条件也可以推导出一个非周期的马尔可夫链是平稳的,因为每次转移状态i从状态j获得的量与 j 从 i 获得的量是一样的,那毫无疑问最后 πT=π.
所以我们的目标就是需要构造这样一个马尔可夫链,使得它最后能够收敛到我们期望的分布 π,而我们的状态集合其实是固定的,所以最终目标就是构造一个合适的 T,就大功告成了。
一般来说我们有:
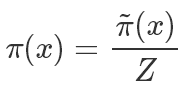
其中Z是归一化参数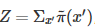 ,因为我们通常能够很方便地计算分子
,因为我们通常能够很方便地计算分子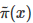 ,但是分母的计算因为要枚举所有的状态所以过于复杂而无法计算。我们希望最终采样出来的样本符合 π 分布。
,但是分母的计算因为要枚举所有的状态所以过于复杂而无法计算。我们希望最终采样出来的样本符合 π 分布。
▌Metropolis
原理描述
Metropolis 算法算是 MCMC 的开山鼻祖了,它这里假设我们已经有了一个状态转移概率函数T来表示转移概率,T(a,b) 表示从 a 转移到 b 的概率(这里T的选择我们稍后再说),显然通常情况下一个T是不满足细致平稳条件的:
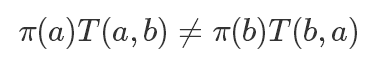
所以我们需要进行一些改造,加入一项 Q 使得等式成立:
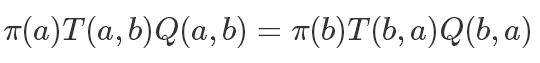
基于对称的原则,我们直接让
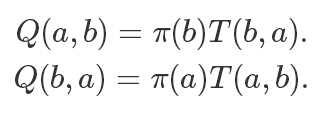
所以我们改造后的满足细致平稳条件的转移矩阵就是:
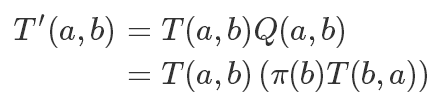
在 Metropolis 算法中,这个加入的这个 Q 项是此次转移的接受概率,是不是和拒绝采样有点神似。

但这里还有一个问题,我们的接受概率 Q 可能会非常小,而且其中还需要精确计算出 π(x′),这个我们之前提到了是非常困难的,再回到我们的细致平稳条件:
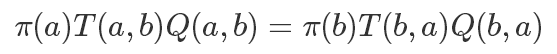
如果两边同时乘以一个数值,它也是成立的,比如
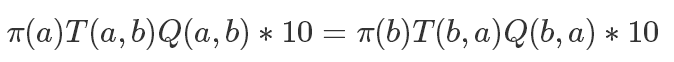
所以我们可以同步放大Q(a,b)和Q(b,a),使得其中最大的一个值为1,也就是说:
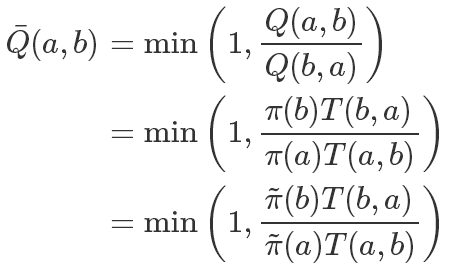
这样在提高接受率的同时,因为除式的存在我们还可以约掉难以计算的 Z。

代码实验
我们之前提到状态转移函数T的选择,可以看到如果我们选择一个对称的转移函数,即 T(a,b)=T(b,a),上面的接受概率还可以简化为
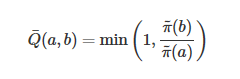
这也是一般 Metropolis 算法中采用的方法,T使用一个均匀分布即可,所有状态之间的转移概率都相同。
实验中我们使用一个二元高斯分布来进行采样模拟
其概率密度函数这样计算的,x是一个二维坐标:
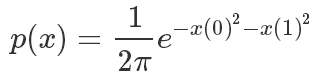
def get_p(x): # 模拟pi函数 return 1/(2*PI)*np.exp(- x[0]**2 - x[1]**2)def get_tilde_p(x): # 模拟不知道怎么计算Z的PI,20这个值对于外部采样算法来说是未知的,对外只暴露这个函数结果 return get_p(x)*20
每轮采样的函数:
def domain_random(): #计算定义域一个随机值 return np.random.random()*3.8-1.9def metropolis(x): new_x = (domain_random(),domain_random()) #新状态 #计算接收概率 acc = min(1,get_tilde_p((new_x[0],new_x[1]))/get_tilde_p((x[0],x[1]))) #使用一个随机数判断是否接受 u = np.random.random() if u
然后就可以完整地跑一个实验了:
def testMetropolis(counts = 100,drawPath = False): plotContour() #可视化 #主要逻辑 x = (domain_random(),domain_random()) #x0 xs = [x] #采样状态序列 for i in range(counts): xs.append(x) x = metropolis(x) #采样并判断是否接受 #在各个状态之间绘制跳转的线条帮助可视化 if drawPath: plt.plot(map(lambda x:x[0],xs),map(lambda x:x[1],xs),'k-',linewidth=0.5) ##绘制采样的点 plt.scatter(map(lambda x:x[0],xs),map(lambda x:x[1],xs),c = 'g',marker='.') plt.show() pass
可以看到采样结果并没有想象的那么密集,因为虽然我们提高了接受率,但还是会拒绝掉很多点,所以即使采样了5000次,绘制的点也没有密布整个画面。
▌Gibbs Sampling
算法分析
通过分析 Metropolis 的采样轨迹,我们发现前后两个状态之间并没有特别的联系,新的状态都是从 T 采样出来的,而因为原始的分布很难计算,所以我们选择的T是均匀分布,因此必须以一个概率进行拒绝,才能保证最后收敛到我们期望的分布。
如果我们限定新的状态只改变原状态的其中一个维度,即
只改变了其中第 j 个维度,则有
其中
结论很清晰:这样一个转移概率函数T是满足细致平稳条件的,而且和Metropolis里面不同:它不是对称的。
我们能够以 1 为概率接受它的转移结果。
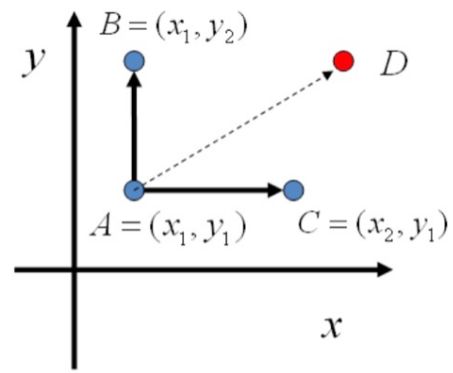
以一个二元分布为例,在平面上:
A 只能跳转到位于统一条坐标线上的 B,C 两个点,对于 D,它无法一次转移到达,但是可以通过两次变换到达,仍然满足 Irreducible 的条件。
这样构造出我们需要的转移概率函数T之后,就直接得到我们的 Gibbs 采样算法了:
代码实验
想必大家发现了,如果要写代码,我们必须要知道如何从
在我们之前实验的场景(二元正态分布),确实也能精确地写出这个概率分布的概率密度函数(也是一个正态分布)。
但退一步想,现在我们只关心一元的采样了,所以其实是有很多方法可以用到的,比如拒绝采样等等。
而最简单的,直接在这一维度上随机采几个点,然后按照它们的概率密度函数值为权重选择其中一个点作为采样结果即可。
代码里这样做的目的主要是为了让代码足够简单,只依赖一个均匀分布的随机数生成器。
def partialSampler(x,dim): xes = [] for t in range(10): #随机选择10个点 xes.append(domain_random()) tilde_ps = [] for t in range(10): #计算这10个点的未归一化的概率密度值 tmpx = x[:] tmpx[dim] = xes[t] tilde_ps.append(get_tilde_p(tmpx)) #在这10个点上进行归一化操作,然后按照概率进行选择。 norm_tilde_ps = np.asarray(tilde_ps)/sum(tilde_ps) u = np.random.random() sums = 0.0 for t in range(10): sums += norm_tilde_ps[t] if sums>=u: return xes[t]
主程序的结构基本上和之前是一样的,
def gibbs(x): rst = np.asarray(x)[:] path = [(x[0],x[1])] for dim in range(2): #维度轮询,这里加入随机也是可以的。 new_value = partialSampler(rst,dim) rst[dim] = new_value path.append([rst[0],rst[1]]) #这里最终只画出一轮轮询之后的点,但会把路径都画出来 return rst,pathdef testGibbs(counts = 100,drawPath = False): plotContour() x = (domain_random(),domain_random()) xs = [x] paths = [x] for i in range(counts): xs.append([x[0],x[1]]) x,path = gibbs(x) paths.extend(path) #存储路径 if drawPath: plt.plot(map(lambda x:x[0],paths),map(lambda x:x[1],paths),'k-',linewidth=0.5) plt.scatter(map(lambda x:x[0],xs),map(lambda x:x[1],xs),c = 'g',marker='.') plt.show()
采样的结果:
其转移的路径看到都是与坐标轴平行的直线,并且可以看到采样 5000 词的时候跟 Metropolis 相比密集了很多,因为它没有拒绝掉的点。
▌后注
本文我们讲述了MCMC里面两个最常见的算法 Metropolis和Gibbs Sampling,以及它们各自的实现
从采样路径来看:
Metropolis 是完全随机的,以一个概率进行拒绝;
而 Gibbs Sampling 则是在某个维度上进行转移。
如果我们仍然希望最后使用独立同分布的数据进行蒙特卡洛模拟,只需要进行多次 MCMC,然后拿每个 MCMC 的第 n 个状态作为一个样本使用即可。
完整的代码见链接:
https://github.com/justdark/dml/blob/master/dml/tool/mcmc.py
因为从头到尾影响分布的只有 get_p() 函数,所以如果我们想对其他分布进行实验,只需要改变这个函数的定义就好了,比如说我们对一个相关系数为0.5 的二元正态分布,只需要修改 get_p() 函数:
def get_p(x): return 1/(2*PI*math.sqrt(1-0.25))*np.exp(-1/(2*(1-0.25))*(x[0]**2 -x[0]*x[1] + x[1]**2))
就可以得到相应的采样结果:
而且因为这里并不要求p是一个归一化后的分布,可以尝试任何>0的函数,比如
def get_p(x): return np.sin(x[0]**2 + x[1]**2)+1
也可以得到采样结果:
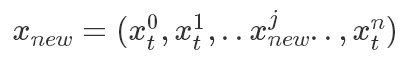
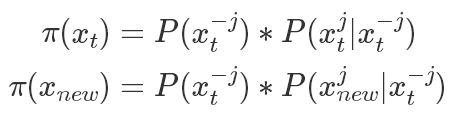
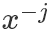 表示除了第j元其他的变量。 所以有(以
表示除了第j元其他的变量。 所以有(以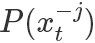 为桥梁作转换很好得到):
为桥梁作转换很好得到): 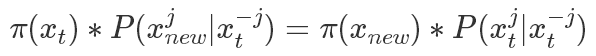


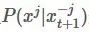 进行采样,这是一个后验的概率分布,在很多应用中是能够定义出函数表达的。
进行采样,这是一个后验的概率分布,在很多应用中是能够定义出函数表达的。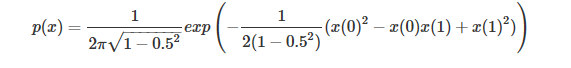
-
 寒天喻晓
2020-12-15
0 回复 举报直接用randn生成服从正态分布的随机数不就好了吗为什么要这么麻烦? 收起回复
寒天喻晓
2020-12-15
0 回复 举报直接用randn生成服从正态分布的随机数不就好了吗为什么要这么麻烦? 收起回复
-
示波器采样时间怎么设置 示波器的采样率有什么意义?2023-10-17 3629
-
请问A/D采样的调试方法有哪些?2019-09-11 0
-
STM32F中AD采样的方法有哪些2021-08-18 0
-
AD采样的方法有哪几种?2021-11-23 0
-
经典的软件滤波方法2009-04-17 1138
-
用于图像分类的有偏特征采样方法2012-03-22 685
-
传统的模拟电压采样保持电路方案2012-04-01 7617
-
10种经典的软件滤波方法2017-01-22 780
-
10种AD采样的软件滤波方法及例程2017-02-15 1074
-
空间曲线基于内在几何量的均匀采样方法2021-04-22 682
-
随机采样方法拒绝采样思想2021-10-14 979
-
AN059 提高ADC采样精度的方法2023-03-01 521
-
每周经典电路分析:采样保持放大器(2)2023-10-13 791
-
非常经典的FPGA设计方法论.zip2022-12-30 232
-
示波器实时采样与等效采样有何区别2023-12-21 1065
全部0条评论

快来发表一下你的评论吧 !

