

焊接温度场仿真和热变形、应力仿真的基本理论和仿真流程
制造/封装
描述
1 前言
焊接作为现代制造业必不可少的工艺,在材料加工领域一直占有重要地位。焊接是一个涉及到电弧物理、传热、冶金和力学等各学科的复杂过程,其涉及到的传热过程、金属的融化和凝固、冷却时的相变、焊接应力和变形等是企业制造部门和设计人员关心的重点问题。焊接过程中产生的焊接应力和变形,不仅影响焊接结构的制造过程,而且还影响焊接结构的使用性能。这些缺陷的产生主要是焊接时不合理的热过程引起的。由于高能量的集中的瞬时热输入,在焊接过程中和焊后将产生相当大的残余应力和变形,影响结构的加工精度和尺寸的稳定性。因此对于焊接温度场合应力场的定量分析、预测有重要意义。
传统的焊接温度场和应力测试依赖于设计人员的经验或基于统计基础的半经验公式,但此类方法带有明显的局限性,对于新工艺无法做到前瞻性的预测,从而导致实验成本急剧增加,因此针对焊接采用数值模拟的方式体现出了巨大优势。
ANSYS作为世界知名的通用结构分析软件,提供了完整的分析功能,完备的材料本构关系,为焊接仿真提供了技术保障。文中以ANSYS为平台,阐述了焊接温度场仿真和热变形、应力仿真的基本理论和仿真流程,为企业设计人员提供了一定的参考。
2 焊接数值模拟理论基础
焊接问题中的温度场和应力变形等最终可以归结为求解微分方程组,对于该类方程求解的方式通常为两大类:解析法和数值法。由于只有在做了大量简化假设,并且问题较为简单的情况下,才可能用解析法得到方程解,因此对于焊接问题的模拟通常采用数值方法。在焊接分析中,常用的数值方法包括:差分法、有限元法、数值积分法、蒙特卡洛法。
差分法:差分法通过把微分方程转换为差分方程来进行求解。对于规则的几何特性和均匀的材料特性问题,编程简单,收敛性好。但该方法往往仅局限于规则的差分网格(正方形、矩形、三角形等),同时差分法只考虑节点的作用,而不考虑节点间单元的贡献,常常用来进行焊接热传导、氢扩散等问题的研究。
有限元法:有限元法是将连续体转化为由有限个单元组成的离散化模型,通过位移函数对离散模型求解数值解。该方法灵活性强,适用范围广,因此广泛地应用于焊接热传导、焊接热弹塑性应力、变形和焊接结构的断裂分析等领域。
数值积分法:该方法采用辛普生法则等方式对很难求得原函数的问题进行积分求解,通过该方法避免了求解复杂的原函数问题,同时使用较少的点即可获得较高的精度。
蒙特卡洛法:该方法基于随机模拟技术,对随机过程的问题进行原封不动的数值模拟。
焊接模拟通常基于以上几种理论对焊接热传导、热弹塑性应力等问题进行模拟,而合理的选择热源函数和计算焊后应力等问题则需要设计人员选择合适的数学模型。
2.1 焊接数值模拟常用热源模型
焊接热过程是影响焊接质量和生产率的主要因素之一,因此焊接热过程的准确模拟,是准确进行焊接应力变形分析的前提。早期对于焊接热过程的解析,前人做了大量的理论研究工作,提出了多种热源分布模型:
集中热源:Rosenthai-Rykalin公式
该方法作为典型的解析方法,认为热源集中于一点,此方式仅对于研究区域远离热源时较为适用,同时此方法无法描述热源的分布规律,对于熔合区和热影响区影响较大。
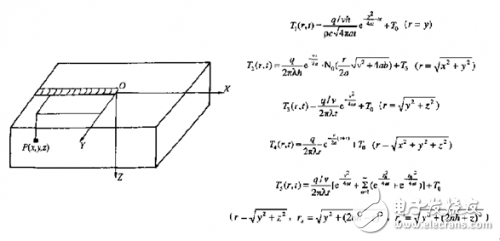
平面分布热源:高斯分布热源、双椭圆分布热源
高斯分布热源
高斯热源分布假设焊接热源具有对称分布的特点,在低速焊接时,效果良好,焊接速度较高时,热源不再对称分布,误差较大。此方法适合于电弧挺度较弱及电弧对熔池冲击较小的情况。
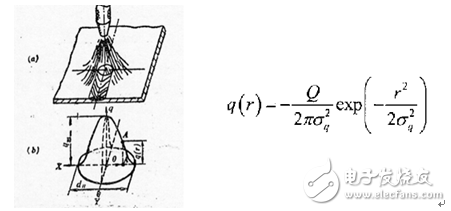
高斯分布虽然给出了热源分布,但没有考虑焊枪移动对热源分布的影响。实际上,由于焊缝加热和冷却的速度不同,因此电弧前方的加热区域比后方的加热区域小。
双椭圆分布热源
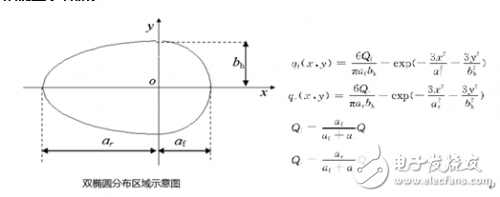
体积分布热源:半椭球分布热源、双椭球分布热源
半椭球分布热源
对于熔化极气体保护电弧焊或高能束流焊,焊接热源的热流密度不光作用在工件表面上,也沿工件厚度方向作用。此时,应该将焊接热源作为体积分布热源。为了考虑电弧热流沿工件厚度方向的分布,可以用椭球体模式来描述
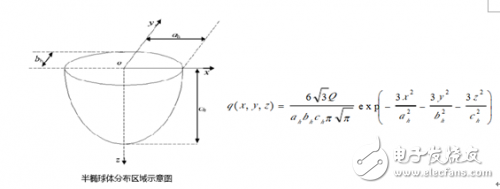
实际上,由于电弧沿焊接方向运动,电弧热流是不对称分布的。由于焊接速度的影响,电弧前方的加热区域要比电弧后方的小;加热区域不是关于电弧中心线对称的单个的半椭球体,而是双半椭球体,并且电弧前、后的半椭球体形状也不相同。
- 相关推荐
- 热点推荐
- 焊接
-
ANSYS软件进行焊接仿真有什么技巧?2019-08-06 8311
-
基于ANSYS的桥面铺装温度场与温度应力模拟分析2009-10-19 615
-
复杂目标红外辐射特性可视化仿真研究2009-12-31 749
-
焊接过程温度场和应力场三维数值仿真技术2010-01-26 675
-
基于ANSYS耦合场分析的电器装置温度场仿真2011-08-11 1116
-
电源管理模式最佳功率仿真的重要性2017-09-25 4800
-
基于CFD的锂电池温度场的仿真模型2017-10-11 1768
-
基于SolidWorks Simulation软件对户外机柜内部的流场、温度场进行计算及仿真分析2017-12-05 3916
-
非均匀温度场下涡旋压缩机涡旋盘数值仿真研究2018-03-15 755
-
应力测试的方法有哪些?功率LED瞬态温度场及热应力分布研究2018-10-24 6664
-
磨削温度场的计算机仿真技术的应用研究2019-10-11 2829
-
基于Fluent的商用车发动机舱过热分析与温度场仿真分析2022-11-21 5137
-
SMT焊接温度曲线智能仿真系统的功能介绍!2024-03-22 1301
-
金属焊接模拟全流程仿真:从初始参数到焊后热处理的完整解决方案2025-04-17 874
-
电磁遇上热与应力-CST多物理场仿真解决复杂工程挑战2025-07-29 697
全部0条评论

快来发表一下你的评论吧 !

