揭秘估算RMS周期间抖动及演示示例

在这篇文章中，我将回顾一个经验法则，该法则可用于估算RMS周期间抖动，前提是你知道RMS周期抖动。我首先在实验室中观察了这个经验法则，并随后了解了更多。

该经验法则是什么？

该法则很简单。如果周期抖动分布是高斯或正态分布，则周期间抖动可以根据周期抖动估算如下：

Jcc (RMS)= sqrt(3) * Jper (RMS)

我首先在定时知识库文章中记录了这一点，该文章是EstimatingRMS Cycle to Cycle Jitter from RMS Period Jitter (https://www.silabs.com/community/timing/knowledge-base.entry.html/2011/04/11/estimating_rms_cycle-Ab6s)。我今天会花更多时间在这个想法上，并从几个不同的角度来解决这个问题。

问题是什么？

在我们的应用笔记“A Primer On Jitter, Jitter Measurement and Phase-Locked Loops” (https://www.silabs.com/documents/public/application-notes/AN687.pdf)中，下图显示了后处理相位噪声进入定时抖动指标的下列斜率。周期抖动和周期间抖动分别显示为20dBc / dec和40dB / dec斜率的高通滤波器。要记住这样一个有用的例子。

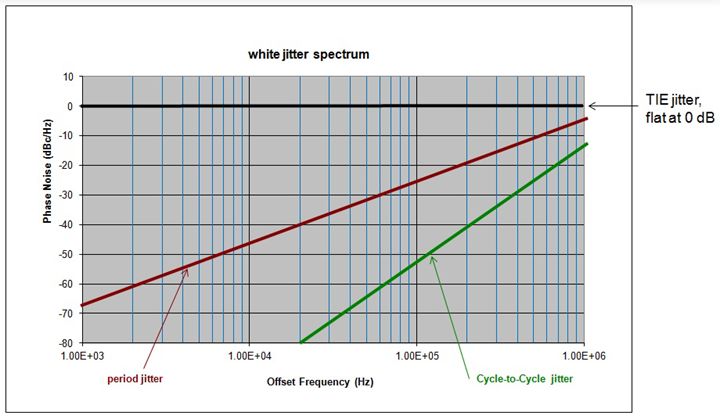
问题是，根据sqrt（3）规则，RMS周期间抖动如何大于RMS周期抖动，并且周期间抖动滤波器的斜率更陡？答案是，决定最终结果的不只是斜率。

重要术语

在继续之前，这里有几个来自AN279:Estimating Period Jitter from Phase Noise（https://www.silabs.com/documents/public/application-notes/AN279.pdf）的定义。

• 周期间抖动 - 相邻时钟周期之间的时钟周期中的短期变化。这种抖动测量（在此缩写为JCC）可以被特指为RMS或峰间量。

• 周期抖动 - 与平均时钟周期相比，所有测量时钟周期内时钟周期的短时变化。这种抖动测量（在此缩写为JPER）可以指定为RMS或峰间量。

实验室测量例子

首先，下面的示例实验测量直接来自知识库文章。为了方便起见，带注释的图像变得更加紧凑。

屏幕截图中有三个项目被调出。

1. 在100万次循环后的周期分布呈现高斯分布，并且非常接近于分别符合±1，±2和±3标准差的68-95-99.7％规则。

2. 测量的RMS周期抖动是周期抖动分布的标准偏差或约1.17 ps。因此，我们可以估算RMS周期以抖动为sqrt（3）*     1.17 ps或2.03 ps。

3. 实际测量的周期到周期抖动为2.05 ps，这与估算值相当接近。

Excel演示示例

您也可以在Excel模拟中演示此规则。为了探索效果，我生成了一个电子表格，其中我选取了一个理想的时钟边缘，然后通过从高斯分布中采集随机样本来抖动边缘。然后，我进行了周期测量和周期间测量，每个周期测量30个边沿，每个边沿100个，时钟边沿表示100MHz时钟抖动。请注意，由于周期间抖动结果是带符号的，即正或负，所以我们应该预期这些量的标准偏差会更大，其他都相等。100个边缘试验通常比30个边缘试验更接近sqrt（3）规则，但即使在30个边缘上仍然可以看到总体效果。

经验法则的解释

那么这个经验法则是如何产生的呢？如前所述，我多年前在实验室首次观察到这一点。然而，我几乎没有看到这方面的文字。最终我找到了StatekTechnical Note 35，An overview of oscillator jitter（http://www.statek.com/products/pdf/TN-35%20Rev%20B.pdf）。下面的解释是这个推导的一个稍微简化和修改的版本，其中数量是“大”时间序列的期望值（回想我对100条边优于30条边收敛的规则）。

让下面的变量代表单个边缘的时间抖动的方差，即抖动边缘与理想边缘的时间差异。

每个测量周期是2个连续边缘值之间的差值，其中每个边缘抖动具有方差s2j。周期抖动有时被称为定时抖动的第一个差异。由于周期间抖动是相邻周期之间的差异，所以它可以被称为定时抖动的第二差异。

如果每个边缘的抖动是独立的，那么周期抖动的方差可以写为：

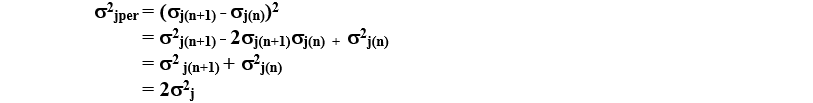
这正是我们所期望的每个“差异总和法”。你可以在这里看到一个例子，它指出了对于独立的（不相关的）变量：

然而，我们不能很容易地计算周期循环抖动，因为在每个周期到周期的测量中，我们使用两次“内部”时钟沿，因此我们必须考虑到这一点。相反，我们写道：

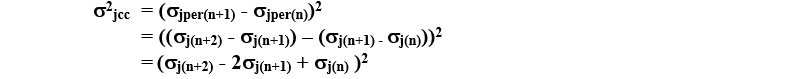
由于每个边缘的抖动被假定为独立的并且具有相同的统计特性，所以我们可以放弃互相关项并写出：

因此，差异的比例

这是一个有趣而意想不到的结果，至少对我来说:)

后处理阶段噪声

AN279:Estimating Period Jitter from Phase Noise（https://www.silabs.com/documents/public/application-notes/AN279.pdf），描述了如何根据对相位噪声积分应用4[sin（pi* f * tau）] ^ 2权重因子，从相位噪声中估计周期抖动。加权因子主要是+20dB / dec高通滤波器，直到在半载波频率达到峰值。

事实证明，您可以使用类似的方法计算周期间抖动。这需要应用主要是+40dB / dec高通滤波器的{4 [sin（pi * f * tau）] ^ 2} ^ 2或16 [sin（pi * f * tau）] ^ 4加权因子，直到在半载频处达到峰值。这正是AN687所指的。

那么如何整合一个更清晰的HPF裙，使得周期间抖动大于周期抖动和sqrt（3）规则？

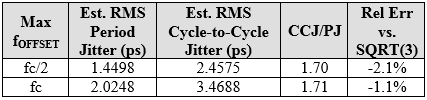
我不得不挖掘我在编写该应用笔记时使用的旧Matlab程序。幸运的是，我仍然拥有该文件和原始数据。然后我运行该程序的修改版本，并比较maxfOFFSET的结果，其中相位噪声数据集在fc / 2和fc处被扩展和截断。答案是，虽然周期到周期的HPF裙子更陡峭，但最大值也更高。看下面的情节。蓝色宽轨迹是周期抖动加权（滤波）相位噪声，红色宽轨迹是周期间抖动加权相位噪声。这是造成差异的更大的远偏移相位噪声贡献。

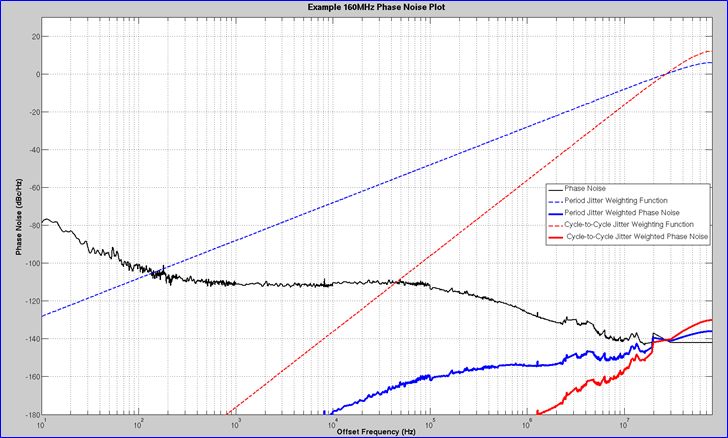
原始数据用于160 MHzCMOS振荡器，其在约2ps时具有示波器测量周期抖动。为了保守，正是出于这个原因，我经常比fc/ 2更进一步地进行整合。现在，示波器的噪声更低，找到待测试的原始设备并在更好的仪器上进行测量会很有趣。我的主要兴趣在于看sqrt（3）关系是否成立。正如你所看到的，两种情况下都遵循经验法则。

结论

我希望你喜欢这篇Timing 101文章。循环周期抖动的sqrt（3）经验法则在实验室，Excel电子表格模拟以及后处理相位噪声时都表现良好。