

主成分分析降维方法和常用聚类方法
电子说
描述
编者按:机器学习开放课程第七课,Snap软件工程师Sergey Korolev讲解了主成分分析降维方法和常用聚类方法。
对CIFAR-10应用t-SNE可视化技术(L2距离)
欢迎来到开放机器学习课程的第七课!
在这节课中,我们将讨论主成分分析(PCA)和聚类(clustering)这样的无监督学习方法。你将学习为何以及如何降低原始数据的维度,还有分组类似数据点的主要方法。
概览
介绍
主成分分析
直觉、理论、应用问题
用例
聚类分析
K均值
近邻传播
谱聚类
凝聚聚类
精确性测度
作业七
相关资源
介绍
和分类、回归方法相比,无监督学习算法的主要特性是输入数据是未标注过的(即没有给定的标签或分类),算法在没有任何铺助的条件下学习数据的结构。这带来了两点主要不同。首先,它让我们可以处理大量数据,因为数据不需要人工标注。其次,评估无监督算法的质量比较难,因为缺乏监督学习所用的明确的优秀测度。
无监督学习中最常见的任务之一是降维。一方面,降维可能有助于可视化数据(例如,t-SNE方法);另一方面,它可能有助于处理数据的多重共线性,为监督学习方法(例如,决策树)准备数据。
主成分分析
直觉、理论、应用问题
主成分分析是最简单、最直观、最频繁使用的降维方法之一,投射数据至其正交特征子空间。
更一般地说,所有观测可以被看成位于初始特征空间的一个子空间上的椭圆,该子空间的新基底与椭圆轴对齐。这一假定让我们移除高度相关的特征,因为基底向量是正交的。在一般情况下,所得椭圆的维度和初始空间的维度相当,但假定数据位于一个维度较小的子空间让我们可以在新投影(子空间)上移除“过多的”空间。我们以“贪婪”方式达成这一点,通过识别散度最大之处循序选择每个椭圆轴。
让我们看下这一过程的数学:
为了将数据的维度从n降至k(k <= n),我们以散度降序给轴列表排序,并移除其中最大的k项。
我们从计算初始特征的散度和协方差开始。这通常基于协方差矩阵达成。根据协方差的定义,两项特征的协方差据下式计算:
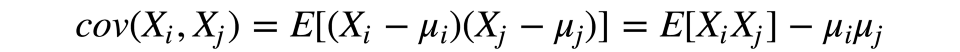
其中,µ是第i项特征的期望值。值得注意的是,协方差是对称的,一个向量自身的协方差等于其散度。
因此,在对角特征的散度上,协方差是对称的。非对角值为相应特征对的协方差。若X是观测的矩阵,则协方差矩阵为:
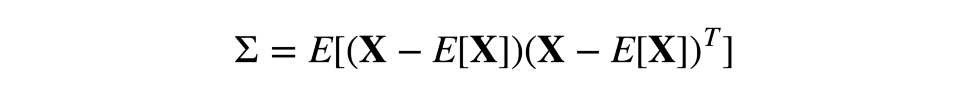
快速温习:作为线性操作的矩阵,有本征值和本征向量。它们非常方便,因为它们描述了我们的空间在应用线性操作时不会翻转只会拉伸的部分;本征向量保持相同的方向,但是根据相应的本征值拉伸。形式化地说,矩阵M、本征向量w、本征值λ满足如下等式:
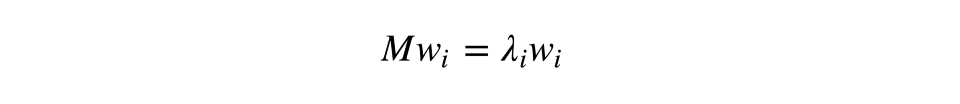
样本X的协方差矩阵可以写成转置矩阵X和X自身的乘积。据Rayleigh quotient,样本的最大差异沿该矩阵的本征向量分布,且和最大本征值相一致。因此,我们打算保留的数据主成分不过是对应矩阵的k个最大本征值的本征向量。
下面的步骤要容易理解一点。我们将数据X矩阵乘以其成分,以得到我们的数据在选中的成分的正交基底上的投影。如果成分的数目小于初始空间维数,记住我们在应用这一转换的过程中会丢失一点信息。
用例
让我们看两个例子。
iris数据集
首先我们先来查看下iris样本:
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns; sns.set(style='white')
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
from sklearn import decomposition
from sklearn import datasets
from mpl_toolkits.mplot3d importAxes3D
# 加载数据集
iris = datasets.load_iris()
X = iris.data
y = iris.target
# 创建美观的3D图
fig = plt.figure(1, figsize=(6, 5))
plt.clf()
ax = Axes3D(fig, rect=[0, 0, .95, 1], elev=48, azim=134)
plt.cla()
for name, label in [('Setosa', 0), ('Versicolour', 1), ('Virginica', 2)]:
ax.text3D(X[y == label, 0].mean(),
X[y == label, 1].mean() + 1.5,
X[y == label, 2].mean(), name,
horizontalalignment='center',
bbox=dict(alpha=.5, edgecolor='w', facecolor='w'))
# 变动标签的顺序
y_clr = np.choose(y, [1, 2, 0]).astype(np.float)
ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=y_clr, cmap=plt.cm.spectral)
ax.w_xaxis.set_ticklabels([])
ax.w_yaxis.set_ticklabels([])
ax.w_zaxis.set_ticklabels([]);
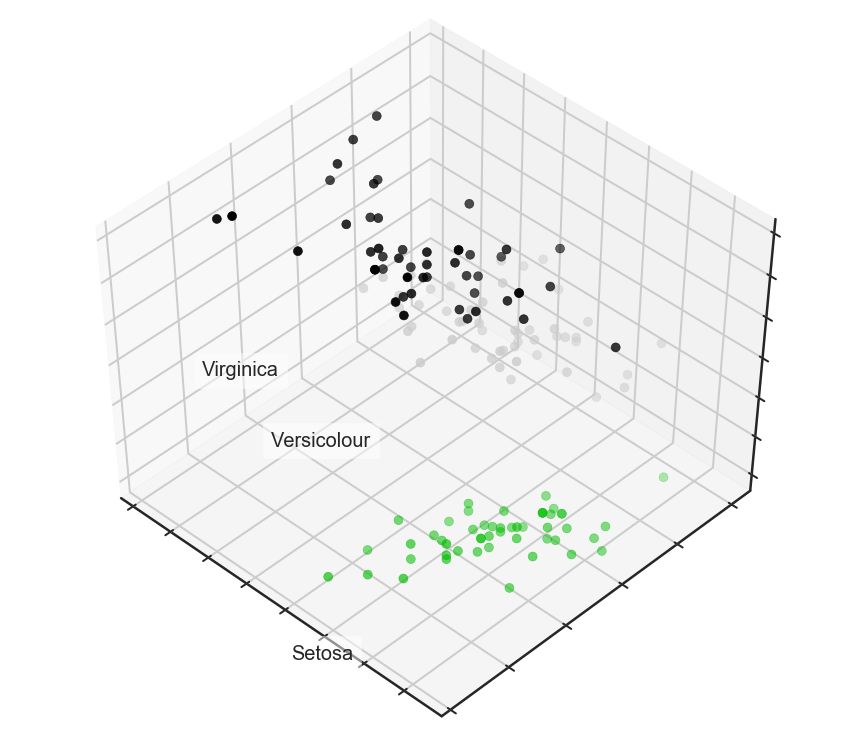
下面让我们看看PCA将如何提高一个不能很好地拟合所有训练数据的简单模型的结果:
from sklearn.tree importDecisionTreeClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, roc_auc_score
# 切分训练集、测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=.3,
stratify=y,
random_state=42)
# 深度为2的决策树
clf = DecisionTreeClassifier(max_depth=2, random_state=42)
clf.fit(X_train, y_train)
preds = clf.predict_proba(X_test)
print('Accuracy: {:.5f}'.format(accuracy_score(y_test,
preds.argmax(axis=1))))
Accuracy: 0.88889
让我们再试一次,不过这回我们将把维数降到2:
# 使用sklearn提供的PCA
pca = decomposition.PCA(n_components=2)
X_centered = X - X.mean(axis=0)
pca.fit(X_centered)
X_pca = pca.transform(X_centered)
# 绘制PCA结果
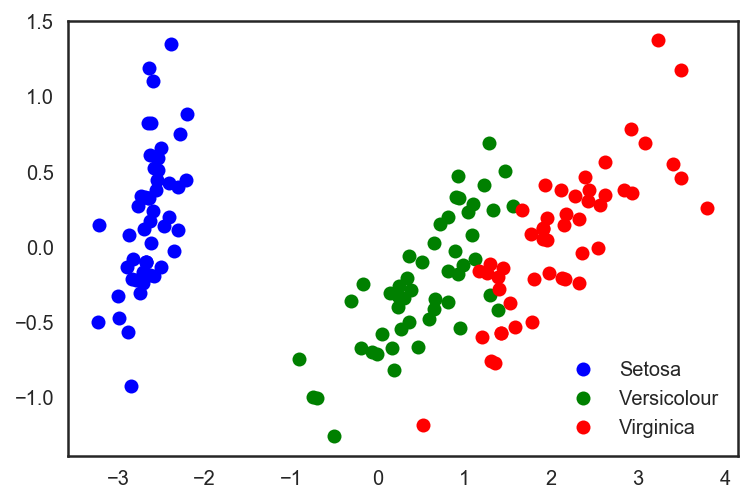
plt.plot(X_pca[y == 0, 0], X_pca[y == 0, 1], 'bo', label='Setosa')
plt.plot(X_pca[y == 1, 0], X_pca[y == 1, 1], 'go', label='Versicolour')
plt.plot(X_pca[y == 2, 0], X_pca[y == 2, 1], 'ro', label='Virginica')
plt.legend(loc=0);
# 分割测试集、训练集,同时应用PCA
X_train, X_test, y_train, y_test = train_test_split(X_pca, y, test_size=.3,
stratify=y,
random_state=42)
clf = DecisionTreeClassifier(max_depth=2, random_state=42)
clf.fit(X_train, y_train)
preds = clf.predict_proba(X_test)
print('Accuracy: {:.5f}'.format(accuracy_score(y_test,
preds.argmax(axis=1))))
Accuracy: 0.91111
在这个例子中,精确度的增加并不明显。但对其他高维数据集而言,PCA可以戏剧性地提升决策树和其他集成方法的精确度。
现在,让我们查看下可以通过每个选中成分解释的方差百分比。
for i, component in enumerate(pca.components_):
print("{} component: {}% of initial variance".format(i + 1,
round(100 * pca.explained_variance_ratio_[i], 2)))
print(" + ".join("%.3f x %s" % (value, name)
for value, name in zip(component,
iris.feature_names)))
1 component: 92.46% of initial variance 0.362 x sepal length (cm) + -0.082 x sepal width (cm) + 0.857 x petal length (cm) + 0.359 x petal width (cm)
2 component: 5.3% of initial variance 0.657 x sepal length (cm) + 0.730 x sepal width (cm) + -0.176 x petal length (cm) + -0.075 x petal width (cm)
手写数字数据集
让我们看下之前在第3课中用过的手写数字数据集。
digits = datasets.load_digits()
X = digits.data
y = digits.target
让我们从可视化数据开始。获取前10个数字。我们使用由每个像素的亮度值构成的8x8矩阵表示数字。每个矩阵压扁至由64个数字构成的向量,这样我们就得到了数据的特征版本。
# f, axes = plt.subplots(5, 2, sharey=True, figsize=(16,6))
plt.figure(figsize=(16, 6))
for i in range(10):
plt.subplot(2, 5, i + 1)
plt.imshow(X[i,:].reshape([8,8]), cmap='gray');
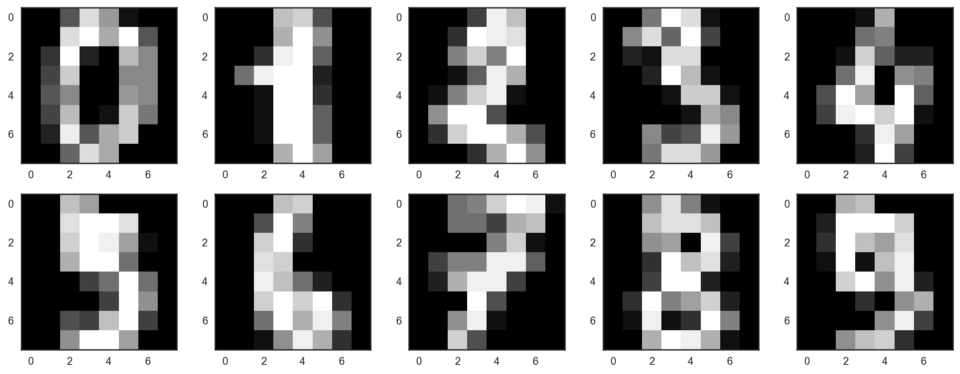
我们的数据有64个维度,不过我们将降维至2维。我们将看到,即使仅有2个维度,我们也可以清楚地看到数字分离为聚类。
pca = decomposition.PCA(n_components=2)
X_reduced = pca.fit_transform(X)
plt.figure(figsize=(12,10))
plt.scatter(X_reduced[:, 0], X_reduced[:, 1], c=y,
edgecolor='none', alpha=0.7, s=40,
cmap=plt.cm.get_cmap('nipy_spectral', 10))
plt.colorbar()
plt.title('MNIST. PCA projection');
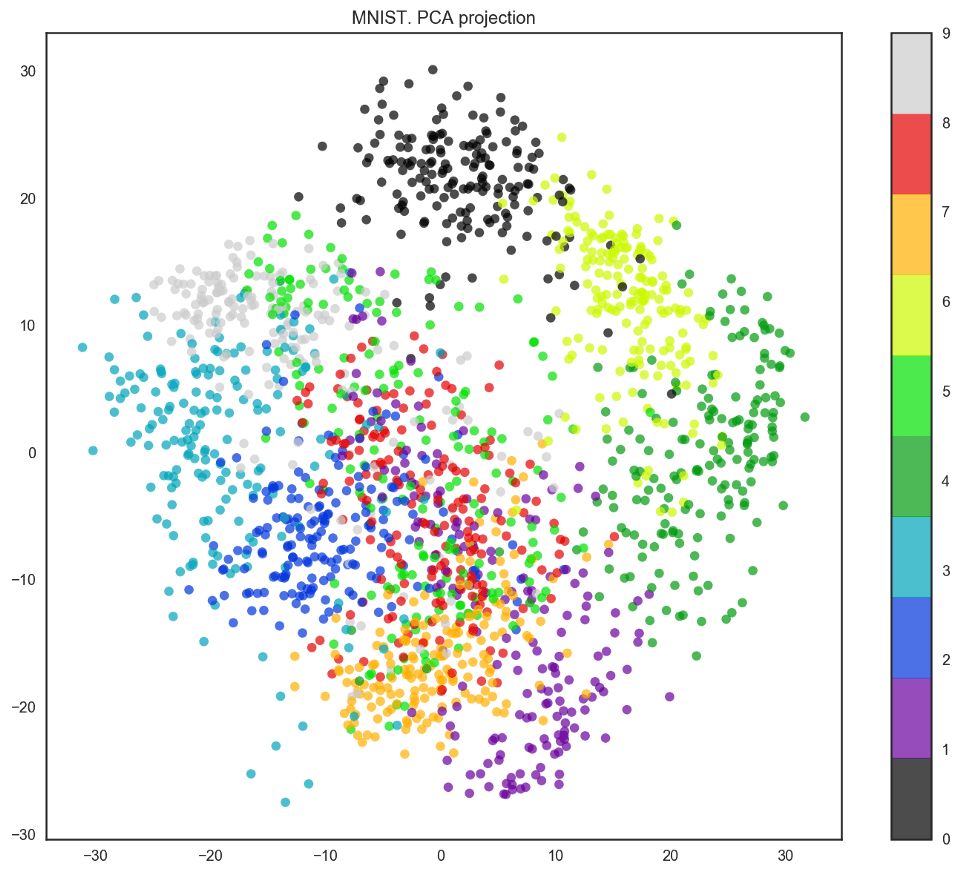
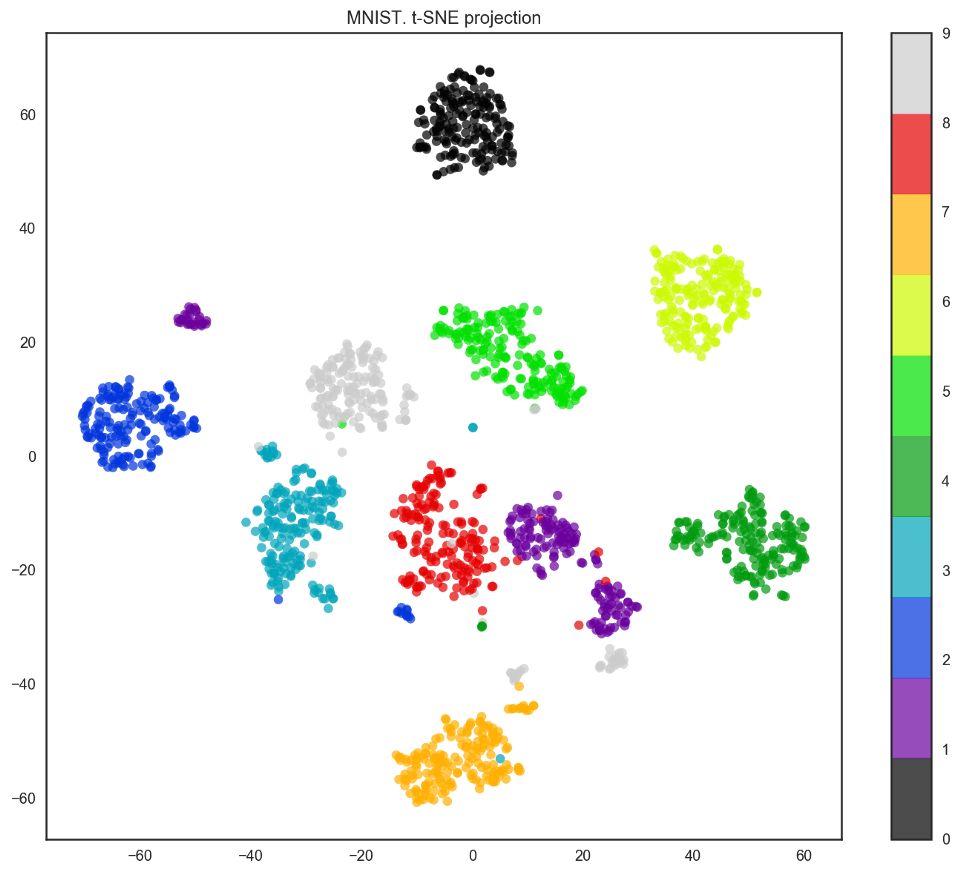
事实上,t-SNE的效果要更好,因为PCA有线性限制,而t-SNE没有。然而,即使在这样一个小数据集上,t-SNE算法的计算时间也明显高于PCA。
from sklearn.manifold import TSNE
tsne = TSNE(random_state=17)
X_tsne = tsne.fit_transform(X)
plt.figure(figsize=(12,10))
plt.scatter(X_tsne[:, 0], X_tsne[:, 1], c=y,
edgecolor='none', alpha=0.7, s=40,
cmap=plt.cm.get_cmap('nipy_spectral', 10))
plt.colorbar()
plt.title('MNIST. t-SNE projection');
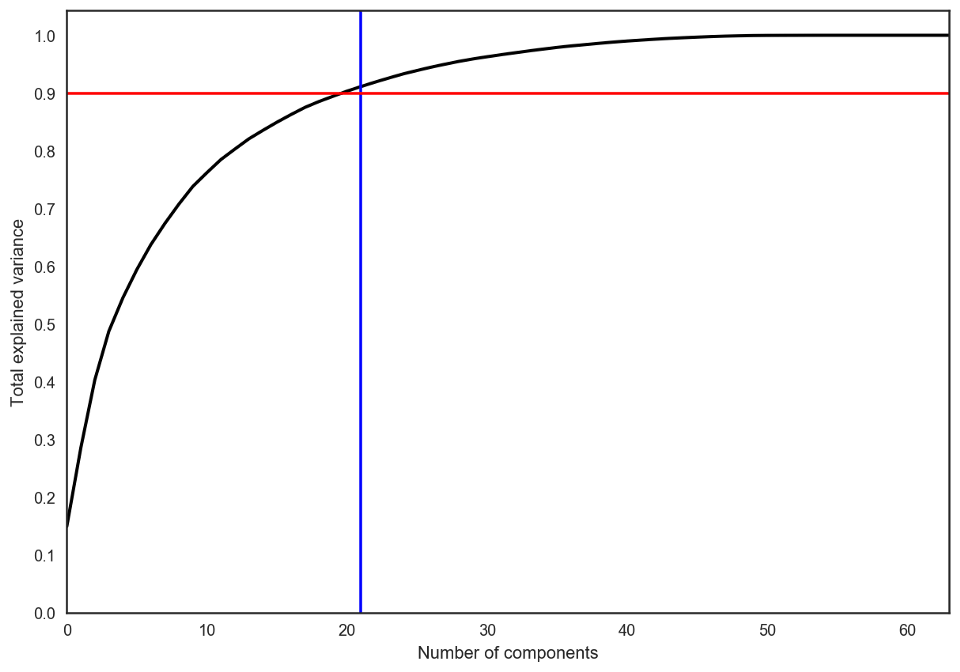
在实践中,我们选择的主成分数目会满足我们可以解释90%的初始数据散度(通过explained_variance_ratio)。在这里,这意味着我们将保留21个主成分;因此,我们将维度从64降至21.
pca = decomposition.PCA().fit(X)
plt.figure(figsize=(10,7))
plt.plot(np.cumsum(pca.explained_variance_ratio_), color='k', lw=2)
plt.xlabel('Number of components')
plt.ylabel('Total explained variance')
plt.xlim(0, 63)
plt.yticks(np.arange(0, 1.1, 0.1))
plt.axvline(21, c='b')
plt.axhline(0.9, c='r')
plt.show();
聚类
聚类背后的主要思路相当直截了当。基本上,我们这样对自己说:“我这里有这些数据点,并且我们可以看到它们的分组。如果能更具体地描述这些就好了,同时,当出现新数据点时,将它分配给正确的分组。”这个通用的想法鼓励探索多种多样的聚类算法。
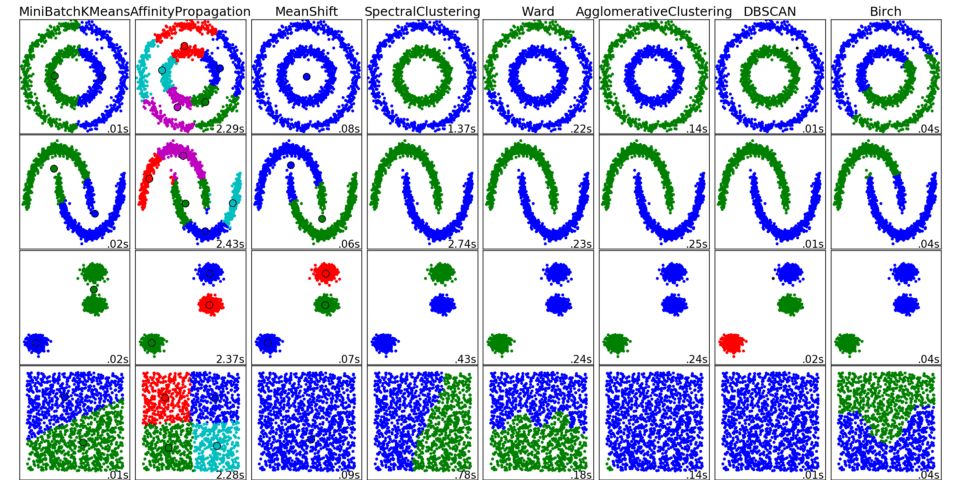
scikit-learn中的不同聚类算法的结果
下面列出的算法没有覆盖所有聚类方法,但它们是最常用的聚类方法。
K均值
在所有聚类算法中,K均值是最流行的,也是最简单的。它的基本步骤为:
选定你认为最优的聚类数k。
在数据空间中随机初始化k点作为“中心点”。
将每个观测分配至最近的中心点。
将中心点更新为所有分配至同一中心点的观测的中心。
重复第3、4步,重复固定次数,或直到所有中心点稳定下来(即在第4步中没有变化)。
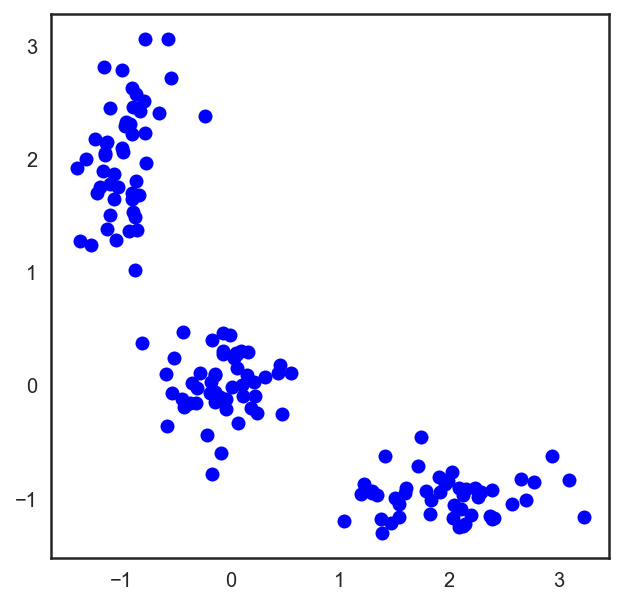
这一算法很容易描述和可视化。
# 让我们从分配3个聚类的点开始。
X = np.zeros((150, 2))
np.random.seed(seed=42)
X[:50, 0] = np.random.normal(loc=0.0, scale=.3, size=50)
X[:50, 1] = np.random.normal(loc=0.0, scale=.3, size=50)
X[50:100, 0] = np.random.normal(loc=2.0, scale=.5, size=50)
X[50:100, 1] = np.random.normal(loc=-1.0, scale=.2, size=50)
X[100:150, 0] = np.random.normal(loc=-1.0, scale=.2, size=50)
X[100:150, 1] = np.random.normal(loc=2.0, scale=.5, size=50)
plt.figure(figsize=(5, 5))
plt.plot(X[:, 0], X[:, 1], 'bo');
# Scipy有一个函数,接受2个元组,返回两者之间的距离
from scipy.spatial.distance import cdist
# 随机分配3个中心点
np.random.seed(seed=42)
centroids = np.random.normal(loc=0.0, scale=1., size=6)
centroids = centroids.reshape((3, 2))
cent_history = []
cent_history.append(centroids)
for i in range(3):
# 计算数据点至中心点的距离
distances = cdist(X, centroids)
# 检查哪个是最近的中心点
labels = distances.argmin(axis=1)
# 根据点的距离标记数据点
centroids = centroids.copy()
centroids[0, :] = np.mean(X[labels == 0, :], axis=0)
centroids[1, :] = np.mean(X[labels == 1, :], axis=0)
centroids[2, :] = np.mean(X[labels == 2, :], axis=0)
cent_history.append(centroids)
# 让我们绘制K均值步骤
plt.figure(figsize=(8, 8))
for i in range(4):
distances = cdist(X, cent_history[i])
labels = distances.argmin(axis=1)
plt.subplot(2, 2, i + 1)
plt.plot(X[labels == 0, 0], X[labels == 0, 1], 'bo', label='cluster #1')
plt.plot(X[labels == 1, 0], X[labels == 1, 1], 'co', label='cluster #2')
plt.plot(X[labels == 2, 0], X[labels == 2, 1], 'mo', label='cluster #3')
plt.plot(cent_history[i][:, 0], cent_history[i][:, 1], 'rX')
plt.legend(loc=0)
plt.title('Step {:}'.format(i + 1));

这里,我们使用了欧几里得距离,不过算法可以通过任何其他测度收敛。你不仅可以改动步骤的数目,或者收敛标准,还可以改动数据点和聚类中心点之间的距离衡量方法。
这一算法的另一项“特性”是,它对聚类中心点的初始位置敏感。你可以多次运行该算法,接着平均所有中心点结果。
选择K均值的聚类数
和分类、回归之类的监督学习任务不同,聚类需要花更多心思在选择优化标准上。使用K均值时,我们通常优化观测及其中心点的平方距离之和。
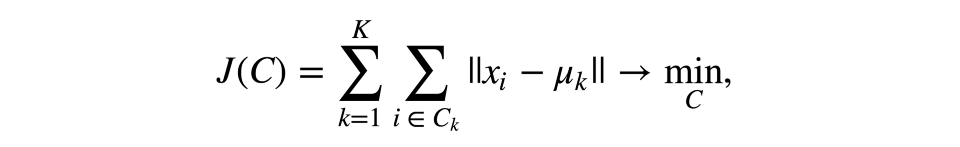
其中C为幂为K的聚类集合,µ为聚类中心点。
这个定义看起来很合理——我们想要观测尽可能地接近其中心点。但是,这里有一个问题——当中心点的数量等于观测的数量时,将达到最优值,所以最终你得到的每个观测自成一个聚类。
为了避免这一情形,我们应该选择聚类数,使这一数字之后的函数J(C)下降得不那么快。形式化一点来说:
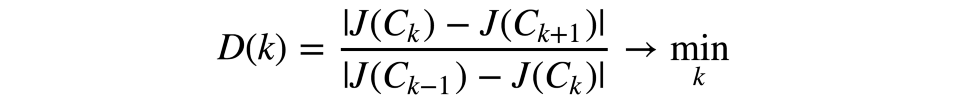
让我们来看一个例子。
from sklearn.cluster importKMeans
inertia = []
for k in range(1, 8):
kmeans = KMeans(n_clusters=k, random_state=1).fit(X)
inertia.append(np.sqrt(kmeans.inertia_))
plt.plot(range(1, 8), inertia, marker='s');
plt.xlabel('$k$')
plt.ylabel('$J(C_k)$');
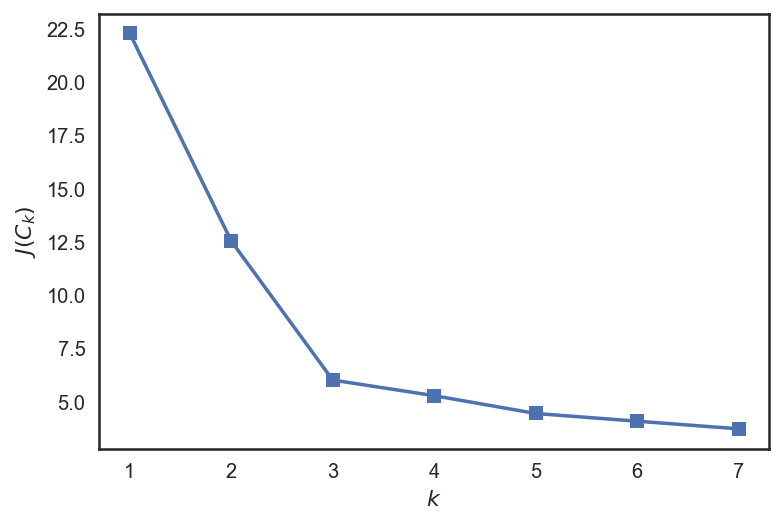
我们可以看到,J(C)在3之前下降得很快,在此之后变化不大。这意味着,聚类的最佳数字是3.
问题
K均值内在地是NP-hard的。对d维、k聚类、n观测而言,算法复杂度为O(n(dk+1))。有一些启发式的算法可以缓解这一问题;例如MiniBatch K均值,分批次处理数据,而不是一下子拟合整个数据集,接着通过对之前的步骤取平均数移动中心点。
scikit-learn的实现有一些优势,例如可以使用n_init函数参数声明初始化数,让我们识别更有鲁棒性的中心点。此外,算法可以并行运行,以减少计算时间。
近邻传播
近邻传播是聚类算法的另一个例子。和K均值不同,这一方法不需要我们事先设定聚类的数目。这一算法的主要思路是我们将根据观测的相似性(或者说,它们“符合”彼此的程度)聚类数据。
让我们定义一种相似性测度,对观测x、y、z而言,若x更接近y,而非z,那么s(x, y) > s(x, z)。s的一个简单例子是负平方距离s(x, y) = - ||x-y||2。
现在让我们通过两个矩阵来描述“相符程度”。其中一个矩阵ri,k将决定,相比七塔寺所有可能的“角色模型”,第k个观测是第i个观测的“角色模型”的合适程度。另一个矩阵ai,k将决定,第i个观测选择第k个观测作为“角色模型”的合适程度。这可能听起来有点困惑,但如果你自己想一个例子实际操作一下,就要好理解得多。
矩阵根据如下规则依次更新:
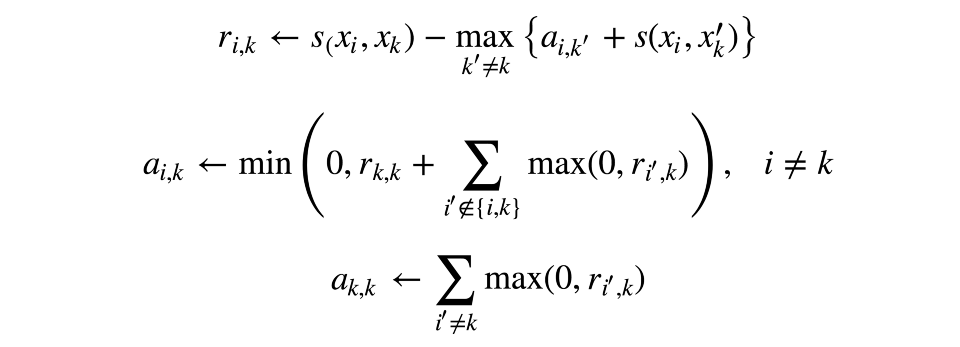
谱聚类
谱聚类组合了上面描述过的一些方法,创建了一种更强劲的聚类方法。
首先,该算法需要我们定义观测的相似性矩阵——邻接矩阵。这一步可以使用和近邻传播类似的方法做到,所以矩阵A将储存相应数据点之间的负平方距离。该矩阵描绘了一整张图,其中观测为顶点,每对观测之间的估计相似值为这对顶点间的边。就上面定义的测度和二维观测而言,这是相当直观的——如果两个观测之间的边最短,那么这两个观测相似。我们将把图分割为两张子图,满足以下条件:每张子图中的每个观测和这张子图中的另一个观测相似。形式化地说,这是一个Normalized cuts问题;建议阅读以下论文了解具体细节:
http://people.eecs.berkeley.edu/%7Emalik/papers/SM-ncut.pdf
凝聚聚类
在不使用固定聚类数目的聚类算法中,该算法是最简单、最容易理解的。
这一算法相当简单:
刚开始,每个观测自成其聚类
根据聚类中心两两距离降序排列
合并最近的两个相邻聚类,然后重新计算中心
重复第2、3步直到所有数据合并为一个聚类
搜索最近聚类有多种方法:
单链(Single linkage)
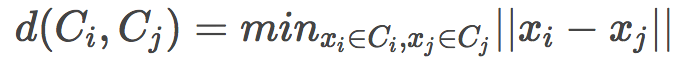
全链(Complete linkage)
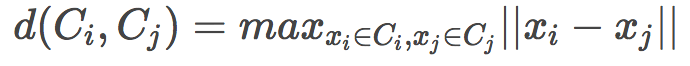
平均链(Average linkage)
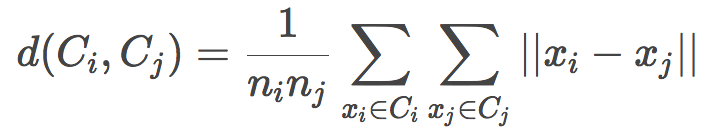
中心链(Centroid linkage)
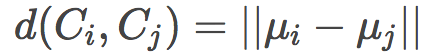
其中,第三个方法是最有效率的做法,因为它不需要在每次聚类合并后重新计算距离。
凝聚聚类的结果可以可视化为美观的聚类树(树枝形结构联系图),帮助识别算法应该停止的时刻,以得到最有结果。有很多Python工具可以构建这样的树枝形结构联系图。
让我们考虑之前的K均值聚类一节中所用的例子:
from scipy.cluster import hierarchy
from scipy.spatial.distance import pdist
X = np.zeros((150, 2))
np.random.seed(seed=42)
X[:50, 0] = np.random.normal(loc=0.0, scale=.3, size=50)
X[:50, 1] = np.random.normal(loc=0.0, scale=.3, size=50)
X[50:100, 0] = np.random.normal(loc=2.0, scale=.5, size=50)
X[50:100, 1] = np.random.normal(loc=-1.0, scale=.2, size=50)
X[100:150, 0] = np.random.normal(loc=-1.0, scale=.2, size=50)
X[100:150, 1] = np.random.normal(loc=2.0, scale=.5, size=50)
distance_mat = pdist(X) # pdist计算上三角距离矩阵
Z = hierarchy.linkage(distance_mat, 'single') # linkage为凝聚聚类算法
plt.figure(figsize=(10, 5))
dn = hierarchy.dendrogram(Z, color_threshold=0.5)
精确性测度
和分类相反,很难评估聚类所得结果的质量。这里,测度无法依赖于标签,只能取决于分割的质量。其次,当我们进行聚类时,我们通常不具备观测的真实标签。
质量测度分为内、外部。外部测度使用关于已知真实分割的信息,而内部测度不使用任何外部信息,仅基于初始数据评估聚类的质量。聚类的最优数目通常根据某些内部测度决定。
所有下面的测度都包含在sklearn.metrics中。
调整兰德指数(ARI)
这里,我们假定目标的真实标签是已知的。令N为样本中的观测数,a为标签相同、位于同一聚类中的观测对数,b为标签不同、位于不同聚类中的观测数。兰德指数可由下式得出:
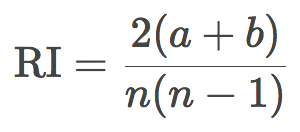
换句话说,兰德指数评估分割后的聚类结果和初始标签一致的比例。为了让任意观测数、聚类数的兰德指数接近零,我们有必要缩放其大小,由此得到了调整兰德指数:
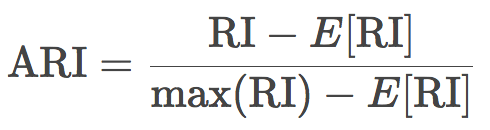
这一测度是对称的,不受标签排列的影响。因此,该指数是不同样本分割距离的衡量。ARI的取值范围是[-1, 1],负值意味着分割更独立,正值意味着分割更一致(ARI = 1意味着分割完全一致)。
调整互信息(AMI)
这一测度和ARI相似。它也是对称的,不受标签的具体值及排列的影响。它由熵函数定义,将样本分割视作离散分布。MI指数定义为两个分布的互信息,这两个分布对应于样本分割聚类。直观地说,互信息衡量两个聚类分割共享的信息量,即,关于其中之一的信息在多大程度上可以降低另一个的不确定性。
AMI的定义方式和ARI类似。这让我们可以避免因聚类数增长而导致的MI指数增长。AMI的取值范围为[0, 1]。接近零意味着分割更独立,接近1意味着分割更相似(AMI = 1意味着完全一致)。
同质性、完整性、V-measure
形式化地说,这些测度同样基于熵函数和条件熵函数定义,将样本分割视作离散分布:
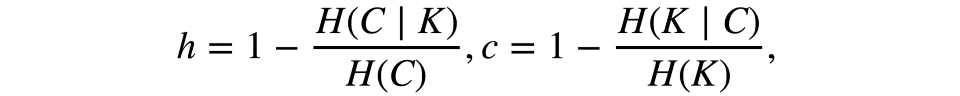
其中K为聚类结果,C为初始分割。因此,h评估是否每个聚类由相同分类目标组成,而c评估相同分类买的物品分属聚类的匹配程度。这些测度不是对称的。两者的取值范围均为[0, 1],接近1的值暗示更精确的聚类结果。这些测度的值不像ARI或AMI一样缩放过,因此取决于聚类数。当一个随机聚类结果的聚类数足够大,而目标数足够小时,这一测度的值不会接近零。在这样的情形下,使用ARI要更合理。然而,当观测数大于100而聚类数小于10时,这一问题并不致命,可以忽略。
V-measure结合了h和c,为h和c的调和平均数:v = (2hc)/(h + c)。它是对称的,衡量两个聚类结果的一致性。
轮廓
和之前描述的测度都不一样,轮廓系数(silhouette coefficient)无需目标真实标签的知识。它让我们仅仅根据未标注的初始样本和聚类结果估计聚类的质量。首先,为每项观测计算轮廓系数。令a为某目标到同一聚类中的其他目标的平均距离,又令b为该目标到最近聚类(不同于该目标所属聚类)中的目标的平均距离,则该目标的轮廓系数为:
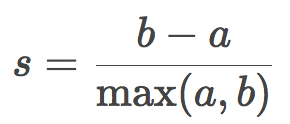
样本的轮廓系数为样本中所有数据点的轮廓系数的均值。该系数的取值范围为[-1, 1],轮廓系数越高,意味着聚类的结果越好。
轮廓系数有助于确定聚类数k的最佳值:选取最大化轮廓系数的聚类数。
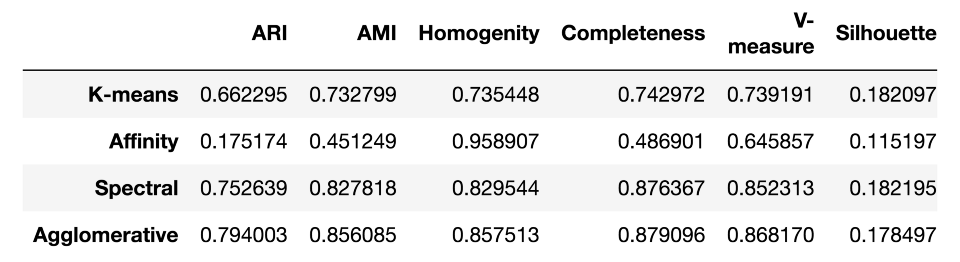
作为总结,让我们看看这些测度在MNIST手写数字数据集上的效果如何:
from sklearn import metrics
from sklearn import datasets
import pandas as pd
from sklearn.cluster importKMeans, AgglomerativeClustering, AffinityPropagation, SpectralClustering
data = datasets.load_digits()
X, y = data.data, data.target
algorithms = []
algorithms.append(KMeans(n_clusters=10, random_state=1))
algorithms.append(AffinityPropagation())
algorithms.append(SpectralClustering(n_clusters=10, random_state=1,
affinity='nearest_neighbors'))
algorithms.append(AgglomerativeClustering(n_clusters=10))
data = []
for algo in algorithms:
algo.fit(X)
data.append(({
'ARI': metrics.adjusted_rand_score(y, algo.labels_),
'AMI': metrics.adjusted_mutual_info_score(y, algo.labels_),
'Homogenity': metrics.homogeneity_score(y, algo.labels_),
'Completeness': metrics.completeness_score(y, algo.labels_),
'V-measure': metrics.v_measure_score(y, algo.labels_),
'Silhouette': metrics.silhouette_score(X, algo.labels_)}))
results = pd.DataFrame(data=data, columns=['ARI', 'AMI', 'Homogenity',
'Completeness', 'V-measure',
'Silhouette'],
index=['K-means', 'Affinity',
'Spectral', 'Agglomerative'])
results
-
薄膜材料成分分析方法2011-01-10 712
-
分享主成分分析源码2012-05-13 5015
-
深入认识主成分分析2019-09-26 1221
-
基于双向二维主成分分析的掌纹识别2009-12-16 913
-
基于Contourlet变换和主成分分析的高光谱数据噪声消除2010-02-10 890
-
主成分分析的图像压缩与重构2012-04-05 981
-
改进主成分分析贝叶斯判别方法2017-12-01 1168
-
关于机器学习PCA算法的主成分分析2018-06-27 3519
-
可提取非线性结构的子空间聚类方法2021-05-18 1044
-
基于稀疏双向二维主成分分析的人脸识别方法2021-05-24 819
-
基于主成分分析和支持向量机的滚动轴承故障诊断2021-05-31 872
-
基于信息增益和主成分分析的网络入侵检测2021-06-27 986
-
什么是成分分析?2024-11-08 1869
全部0条评论

快来发表一下你的评论吧 !

