线性纠错码的基石——奇偶校验

纠错编码的核心设计思想是通过增加冗余信息，使得原始信息的编码之间有足够大的区别。

编码距离

还记得蛋蛋表白的时候，信息为“我 喜 欢 你”四个字，为了防止女神听不到，他添加了冗余信息。经过蛋蛋添加冗余后变为了“我 我 我 喜 喜 喜 欢 欢欢 你 你 你”，其实女神收到的信号为（我 我 饿 T x x 欢 花 欢 x x 里），其中x表示为邻座大妈的霸气的笑声，女神是如何正确的捕捉到蛋蛋的意图呢？显然女神在这方面很有经验，识破了蛋蛋重复三遍的伎俩，电光火石间，在她脑海里飞速搜索比对推理，得出一个通顺而有意义的结论。换句话说，在女神的词典中，有意义的语句全都列出来，发现跟蛋蛋发出声音最相似的就是：“我我 我 喜 喜 喜 欢 欢 欢 你 你 你“

女神的词典可以看成所有可能编码的集合，如何衡量这个编码集合中，容易混淆的程度呢？这个参数就是编码距离。什么是距离呢，这里指的是汉明距离，指的是两个信号之间有多少bit 不同。比如信号（0，1，1）与（0，0，0）的距离为2，（1，1，1）与（0，0，0）的距离为3.

蛋蛋有4个信息，为00，01，10，11. 现在如何插入冗余呢？

首先想到的是重复法：

q 00 变为 00 00 00 00

q 01 变为 01 01 01 01

q 10 变为 10 10 10 10

q 11 变为 11 11 11 11

现在接收到信号 为 00 01 00 00， 我们发现跟这个信号最相似的是 00 00 00 00，距离为1.

一个编码集合里，大家不一定是均匀分布的，有些编码之间距离比较近，有些比较远，编码距离指的是最近的两个编码之间距离。

解码的时候，一个最暴力的方法就是一一比较接收到的信号和所有有效编码之间的编码距离，选择编码距离最小的。所以编码距离的重要作用是可以指示编码可以纠错的bit个数。蛋蛋和阿呆住在不同的地方，相距为d，蛋蛋养了一群羊，阿呆也养了一群羊。羊会乱跑，显然只要羊跑的距离小于d/2 距离，就可以判断羊属于蛋蛋还是阿呆。所以对纠错码而言，编码距离为d，只要bit翻转个数小于d/2，我们可以根据离得谁近就归谁的原则去纠错（赶羊回家 ）。

线性纠错码的基石——奇偶校验（parity-Check）

收钱的阿姨狐疑地拿起蛋蛋递过来的皱巴巴的100块钱，迎着灯光仔细打量过后，又取出了紫外线灯从头到尾照了一下，终于把钱放进钱盒子里，找了蛋蛋99块5。阿姨担心收到假币，她检查钞票可不敢马虎。

阿姨检查钞票的行为叫做信号校验，信号校验的基本模型是：

对信号进行某种特定的处理后，得到期望的结果是为校验通过，否则校验失败。

这里信号用表示，特定的处理用H表示，表示对信号y进行了处理。处理结果用CR表示。

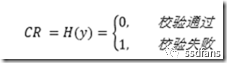
在二进制的世界里，最基础的校验方法是奇偶校验即parity-Check。

对于n bit 二进制信号:

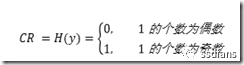
例如长度为16的二进制数据：1000100111011011，其中1的个数为9，故CR = 1。

判断信号里的1的个数为奇还是偶，有非常简单的方法。在二进制里，有一种异或

(即xor)运算，符号为 ，运算方式先进行加法运算，然后运算结果对2取余数（mod（2）），或者更简单的记忆为“相加不进位”：

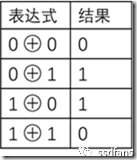
图1 异或运算表达式

可以验证只要把二进制的每一个bit依次进行xor运算，奇数个bit 1的结果为1，偶数个bit 1的结果为0，与bit 0的个数无关。

所以，用 表示第bit i的值（0或1），有

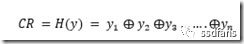
利用奇偶校验可以构造最简单的校验码——单bit校验码SPC（即single bit parity check code）。

把长度为n的二进制信息，增加1 bit 变成y’，使得：

现在y’构成了y的单bit校验码。（a）又叫做奇偶校验方程。

显然，y’中任意一个bit如果发生bit反转，无论从0到1，还是1到0，校验方程 CR = 1 。

SPC 可以探知任意单bit的反转。对于偶数个bit 反转SPC无法探知。而且校验方程并无法知道是bit反转的位置，所以无法纠错。

一个自然的想法是，增加SPC的个数，增加冗余的校验信息。同一个bit被好几个校验方程保护，当它出现错误时候，就不会被漏掉。

后面的文章中，用 + 代替

校验矩阵H 和 生成矩阵G

蛋蛋的丈母娘，在女儿结婚前对未来女婿有一个要求列表，前五条是1）一定是博士学位，2）脾气要好，3）人要长得帅，4）会做家务， 5）财政上交

这样，蛋蛋的丈母娘通过提出要求，就轻而易举实现了对地球上所有男性同胞的一个划分。每一条要求都是一个校验方程。什么样的校验方程组，决定了这个男性同胞群到底有哪些人组成。

多个校验方程可以表示为校验矩阵 H。有了H 就可以确定所有可能的编码。

对于所有x(〖x_0  ,x〗_1  ,x_2,x_3,x_4,x_5…)，只要满足

Hx^T= 0

x 就是合理的编码。如果不满足，x不属于合理的编码，认为在传输的过程中x出现了错误。

举例：长度为4的信号，x(x_0  ,x_1  ,x_2,x_3),有2个校验方程：

x_0+x_2=0

x_1+x_2+x_3=0

现在用 + 代替 ⨁，

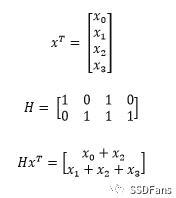
可见，H矩阵里每一行可以表示一个校验方程。行里的1的位置i表示信号中第i bit 参与校验方程。

所有满足奇偶校验方程的x组成了一个编码集合。一般来说，编码长度为n bit，有r个线性独立的校验方程，则可以提供k = （n – r）个有效信息bit，和r个校验bit。

对于线性分组编码而言，原始信号u经过一定的线性变换可以生成纠错码c。完成冗余的添加。线性变换可以写成矩阵的形式，这个矩阵就是生成矩阵G。

表示为，c =uG

c为 n bit 信号。u 为k bit 信号，G 为 k x n 大小的矩阵。由H 矩阵可以推导出生成矩阵G。