信号经过傅立叶变换所得频谱的物理意义

在对任何信号进行傅立叶分析时，得出的频谱为复数，且其频率范围将从-∞~∞。对于负频率以及该范围的频谱，应当如何理解?它有没有物理意义?是一个还缺乏讨论，因而没有统一看法的问题，本文将对此进行讨论。 

摘要：本文讨论了信号经过傅立叶变换所得频谱的物理意义，其中着重于负频率成分。许多信号与系统的教材中，都认为负频率成分没有物理意义。本文以多方面的实例证明了负频率成分不但具有明确的物理意义，而且有重要的工程应用价值。文章还用Matlab程序演示了如何用几何方法求傅立叶反变换，把集总频谱合成为时域信号，从中也可鲜明地看出负频率成分的意义。

1．负频率与复信号

频率 f 的原始定义是每秒出现的次数，可用以衡量机械运动、电信号、乃至任何事件重复出。

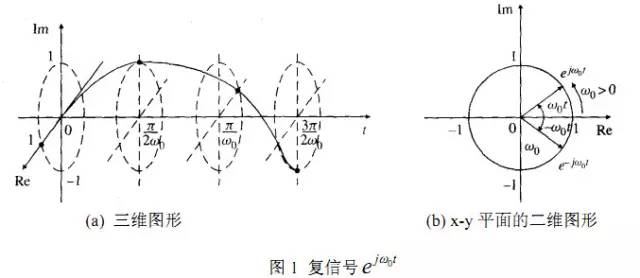
(a) 三维图形                                    

(b)x-y 平面的二维图形现的频度，这当然不存在      

有“负”的概念。当用频率描述圆周运动时（即进入了二维信号平面），产生了角频率 ω”的概念，从机械旋转运动出发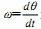，定义为角速度，对于周期运动，角速度也就是角频率。通常 θ以反时针为正，因此转动的正频率是反时针旋转角速度，负频率就是顺时针旋转角速度。正、负号是非常自然形成的，没有物理意义的有无问题。电的单位向量（电压或电流）围绕原点的转动，可以用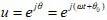表示，这是在电路中都清楚的。θ的正负所代表的物理意义从未有什么争议，它的导数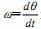的物理意义不言自明，取正取负都不影响定义，为什么取负就会失去物理意义了呢？在信号与系统课程中，为了简化问题，便于初学者掌握概念，开宗明义地把研究范围限定于实 信 号 f(t) ， 也就是 在 电 压 旋 转 向 量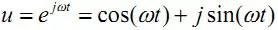

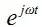
2．复信号与实信号的频谱

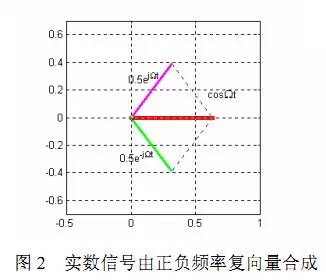
同样，用ejtω或 sin(ωt)或 cos(ωt)作为核来做傅立叶变换所得的结果也是前者全面，后者片面。对实信号做傅立叶变换时，如果用指数为核，将得到双边频谱。以角频率为Ω的余弦信号为例，它有具有位于±Ω两处的、幅度各为 0.5、相角为零的频率特性。它的几何关系可以用图2表示。两个长度为 0.5 的向量，分别以±Ω等速转动，它们的合成向量就是沿实轴方向的余弦向量。而沿虚轴方向的信号为零。可见必须有负频率的向量存在，才可能构成纯 粹的实信 号 。 所以欧公式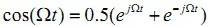

3．双边频谱的工程应用

正余弦信号中包括正负双边频谱，不仅有物理意义，而且具有重要的工程价值。

1）二相异步电机的设计

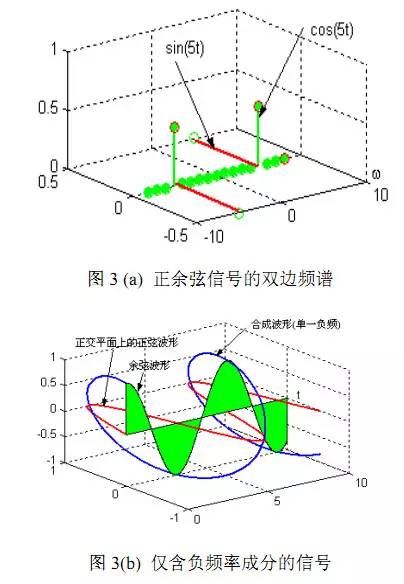
根据这个概念，可以用两路在空间正交的实信号来构成旋转电磁场，设计电动机。上面给出了单位余弦波在正负两个频率上有幅度相等，相角均为零的两根谱线；同样，单位正弦波在同样正负两个频率上也有幅度相等的谱线，不过它们的相角分别为±π/2。用立体图表示如图 3(a)。

如果把正弦和余弦两个信号的正频率成分设计得相等相反，则把它们合成以后，就只剩下负频率成分，它就构成一个单纯负向旋转的电信号。为此可以把正弦信号在空间上转动π/2，使它的正频率谱线恰好与余弦信号的正频率谱线反向，这样两个信号的合成（见图3(b)）就成为一个只有负频率谱线的信号，当然它在时域必然是复数信号。常用的二相异步电机就是这样负向转动的。而要使该电机正转，则要使两者的负频率成分互相抵消，只保留其正频率成分。

2）通信领域中的 Hilbert 变换

实信号的双边频谱是对称的。如果它的单边频带宽 W，考虑到负频率成分，实际占的频谱区域就是±W，所以通信中要传输这样的信号就需要占用 2W的频带宽度。为了节省频带，人们就发明了 Hilbert 变换，它可以把信号的正频率频谱移相-90°，把负频率频谱移相90°，然后再将这个信号移相90°与原信号相加，使两者的负频率成分互相抵消，正频率成分加倍，构成一个没有负频率频谱的复信号,（如同上面所说的二相异步电机那样）。这个复信号的带宽就只占 W 了。用这个方法，使频带节约了一半。在这里，可以看到负频率成分的重要性，在传送信号时。它是不可或缺的部分。另外，也看到负频率成分与复信号的密切关系。 3）产生任意的平面运动轨迹 文献[5]曾提出根据傅立叶反变换原理产生平面运动轨迹的方法。从上面欧拉公式的几何意义不难得知，傅立叶反变换公式其实表示了多个频谱旋转向量的合成，这些向量的频率规定了它信号的实部，在 y轴上的投影是信号的虚部。

不难设计出一个程序来演示这个过程，在[2,3]中编写了一个MATLAB 程序，程序名为 exn941。它把四个集总频谱合成起来。假如给出这些频谱分量如下：

a(1) = 1， ω(1) = 1； a(2) = 1， ω(2) = －1； a(3) = 0.5，ω(3) = 3；a(4) = 0.5，ω(4) = －4；

在此处，为了显示复信号，有意把输入频谱设成不对称的，见图5(d)。于是读者将看到四节杆的运动动画，并得到杆系及其末端在复平面上的轨迹（图4），改变了比例尺后为图 5 (a)。将它在x，y两方向的投影与时间轴的关系画在图5(b)和(c)中，就得到信号与系统课程中常见的实信号曲线。

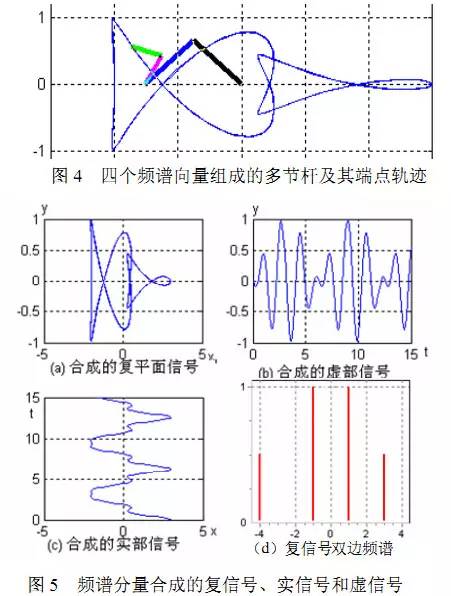
输入频谱的幅度可以是负数，也可以是虚数，甚至可以是复数，它不仅反映了频谱的大小，还反映了该向量的起始相位；频谱的频率则只能是有正负号的实数，正频率和负频率以及在该频率上频谱的意义在此不言自明。读者可以做各种各样的试验。例如当两组频率具有倍频关系时，得到的是周期信号，如果频率比是无理数，那将得出非周期的信号；另外，这样的演示只适用于集总频谱，对于分布的频谱密度，就要把它想象为若干小的集总频谱的叠合。

总之有了这样的形象演示，可以大大扩展时域信号与频域谱之间关系的思维空间。

4）多普勒频率

多普勒频率又是一个负频率的实例，如果信号的发射源向我们运动而来，那么多普勒频率就是正频率；如果信号的发射源向我们远离而去，那么多普勒频率就是负频率，在这里正负频率都是有明确物理意义的。多普勒频率虽是一种差频，它表现为合成信号的包络频率，因此仍然符合上述的原理，在实信号域只能求出多普勒频率的大小，但检测不出它的正负。要得到负频率，必须从复信号域考虑。可见，不懂得这一点，就无法找到多普勒测速的原理框图。

5）机械工程领域的应用

关于二维信号的傅立叶变换，国内早已有学者将其应用于工程领域，参见文献[4]、 [5]。这些都是说明频谱中负频率物理意义的实际例证。

4．在对负频率认识中存在的问题

频谱中负频率成分的物理意义往往不为某些人们理解，其主要原因是他们忘记了实信号平面内研究问题的局限性。因为在信号与系统课程中研究的信号通常只限于实信号。从实信号的x-t的波形图上根本看不出频率的转向和正负，频率只能表现为每秒信号重复的次数。分不清正负就以为是正频率，只是一种习惯性的思维方法而已。

归根到底，转角和频率的正负，必须在x-y平面或二维信号中才能观察到。因为观察的方法不对，看不到其意义，从而否认它的存在，这是认识论上的错误，不是科学的方法。这就和“瞎子摸象”的故事所说的那样，摸象腿的人否认象有鼻子，毛病出在他的验证方法。他老想在象腿（实信号域）上找到象鼻子（负频率），当然也永远找不到。正确的方法是必须换一个角度，摸别的部位（复信号域），才能得到全面的知识。

某些学者不承认负频率是由于把“频率是每秒钟循环的次数”的陈旧概念绝对化，其实频率的概念是不断发展充实的。每秒次数的概念只能粗糙地研究信号外部形态，无法涉及信号每周期内部的细微波形特征，而这恰好是傅立叶变换的任务。从它的核已经可以清楚地看到，正是它摒弃（或发展）了原始的频率定义，采用了角频率的概念。单位是弧度/秒，而且具有明确的方向和正负号。其实频率的概念还在继续发展，进入到数字信号处理时又进一步出现了数字频率，它的单位是弧度（去掉了分母上的“秒”），取值范围是[-π，π]。它的物理意义已变为两次采样时刻之间向量转过的角度，在文献[1]中对此有详细的说明。如果停留在“每秒次数”的旧概念上，那“数字信号处理”也就无法发展了。

5．从认识论角度纠正对负频率的错误说法

这个问题是从教学中提出的，作者在旁听“信号与系统”课程时，在老师的幻灯片上看到了 “关于双边谱，负频率只有数学意义，没有物理意义”的提法。我们觉得这是个错误，而且恐怕不是个别老师的想法。回来一查，果然如此，很多相当权威的主流教材上都这么写。

其实，“×××只有数学意义，没有物理意义”这样的“命题”谁也没有证明过，也是无法证明的，它最多只能算是猜想。只要有一个反例就可被推翻，本文已经举出了多个反例，说明它是完全错误的。教师绝不该把错误的猜想说成真理，更不能写在书上和幻灯片上去误导学生。数学是更抽象、更深刻地描述物理现象的工具，而物理是实证的科学。限于条件，人们往往暂时还认识不到数学定理的物理意义。数学超前物理是科学史上多次出现的现象，比如虚数、非欧氏几何等。这时应该努力去理解它，认识它，而不是轻易地放弃它、否定它。自己没想通，没找到的事物，不能说它不存在。给学生讲课时，只能说“我们目前还没有想通×××的物理意义”。这才能表明教师在科学上的严肃和谦逊，也有助于培养学生的科学钻研和创新精神。

6．结束语

讨论这个问题，不仅是理论上的探讨，对于提高教学质量是有重大意义的。今天，信息技术如此的发展，很大程度是由于深入大量地开发频谱资源的结果。在同学刚进入这个资源库的时候，我们要引导他们对这个宝藏发生极大的兴趣，非常珍惜这个宝藏，去深钻，去挖掘它的每一点潜力。不能为了省事，为了堵住学生的好奇提问，轻率地、毫无根据地一句话就把频谱的负频率半边扔掉了。在入门的时候，当然不可能把本文说的概念统统灌输给学生，要顺序渐进。但老师首先要有更宽广的知识面和更科学的思维方法，教出的学生的才会具备更多的想象力和创造性。