基于高频电磁的寻迹算法升级版介绍

摘要： 虽然一致性几何绕射理论（UTD）理论上可以应用于由非均匀有理B样条（NURBS）建模的任意形状的曲面，但UTD表面衍射场的计算中有一个巨大挑战，即难以确定爬行波在任意形状的NURBS表面上传播的测地线路径。在微分几何中，测地路径满足测地微分方程（GDE）。因此，引入了一种通用且高效的自适应变量欧拉法来解决任意形状的NURBS曲面上的GDE。与传统的欧拉法相比，所提出的方法采用形状因子（SF）ξ来有效提高跟踪精度，并扩展了UTD在实际工程中的应用。 算法的有效性和有用性可以通过数值计算结果进行验证。

0 引言

    在高频电磁问题中，一致性几何绕射理论（UTD）应用非常广泛[1]，例如目标散射特性预估。因此，在准确获得目标表面UTD绕射场问题上，表面爬行射线波追踪起着非常大的作用[2]。所以，首先要进行目标表面爬行波追踪（测地线轨迹）。但是，实际上除了一些典型形体能够直接得到测地线微分方程（GDE）外，在任意形状的光滑物体表面如何测定测地线轨迹是一个巨大的挑战。

    JHA R M[3-5]提出了Geodesic Constant解析方法，但只在一般的抛物旋转面适用。通常地，在工程应用上，很多目标被看作如木板、圆柱、圆锥和球等一些已经有爬行波寻迹解析解的典型形体。但很难用这些典型形体去估计复杂形体，这似乎就限制了UTD方法的应用。

    因此，需要介绍一下数值爬行波追踪算法，该方法基于离散三角面剖分模型表面，但是不能直接应用于UTD算法[6]。除了用离散三角形面片建立复杂模型，它还可以描述NURBS曲面。而且，NURBS曲面由于它的高精度、少面片的特性，被引用到高频电磁分析领域。当目标用NURBS曲面表示后，测地线轨迹可由GDE求解直接获得。所以，一些数值方法被用来计算GDE。为了获得NURBS曲面上的爬行波轨迹[7]，欧拉方法效率高但是精度低，精度依赖于剖分面片外形，对于任意形状模型可能会失效。

    为了提高在任意形状NURBS表面爬行波追踪的准确性和效率，本文提出了一种基于新型自适应变步长欧拉法的爬行波跟踪算法。由于自适应变步长欧拉方法是基于传统的欧拉法，从而保证了效率；并在数值迭代求解GDE的过程中引进形状因子ξ，离散的步长可以及时自适应地纠正。因此，与传统的欧拉法相比，该方法可以很容易地保证其准确性在任意形状的NURBS表面上的爬行光线跟踪。也就是说，它更适合于工程应用。

1 任意形状目标NURBS曲面建模

    非均匀有理B样条(Non-Uniform Rational B-Splines，NURBS)曲面是非均匀B样条曲面的有理推广。它被定义为：

    u、v参数域映射到3个空间可以在图1中看到。

 

 

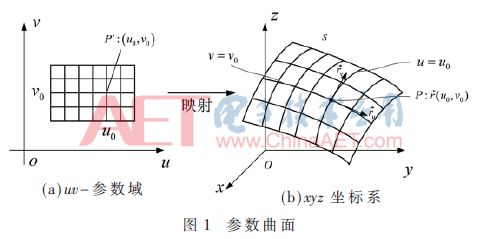
    下面在图2中给出3个NURBS建模结果。其中圆柱的表面是均匀网格表面，而其他表面是不均匀网格表面。

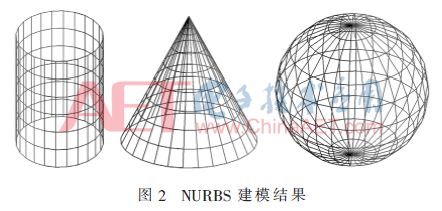
2 任意NURBS曲面表面的爬行波追踪算法

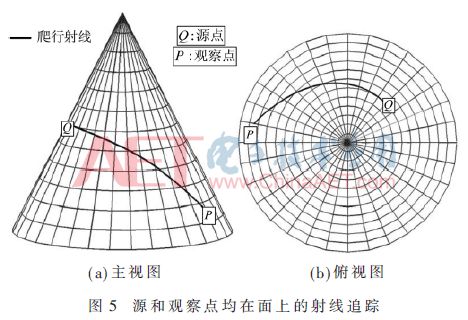
    对于源点和观察点的位置，光滑曲面表面的绕射问题有3种类型：(1)源点和观察点都不在表面且远离表面，这种情况属于光滑曲面散射问题；(2)源点在曲面上，观察点远离表面，此时为光滑曲面辐射问题；(3)源点与观察点都在表面上，这就属于耦合问题[10]。

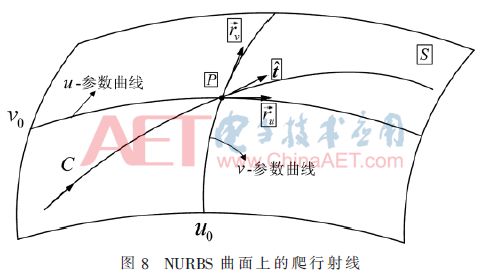
    所以，射线追踪也有3种类型，根据图3～图5所示，在所有这些情况下，表面上的射线轨迹称为爬行波，其被约束沿着测地线传播。本文主要关注爬行波的射线追踪，因为它是射线追踪过程中最困难的一部分。

 

 

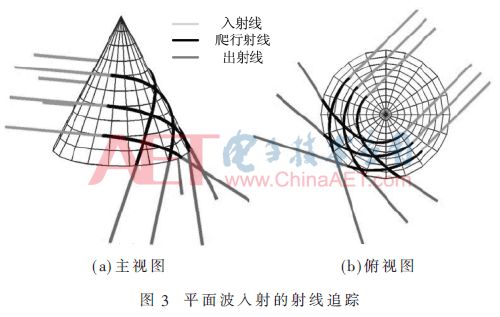
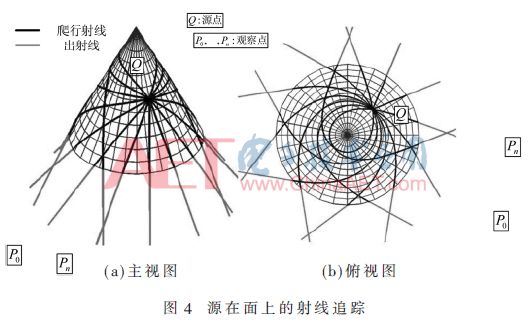
2.1 爬行波的入射点和出射点

    

 

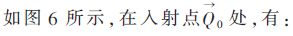
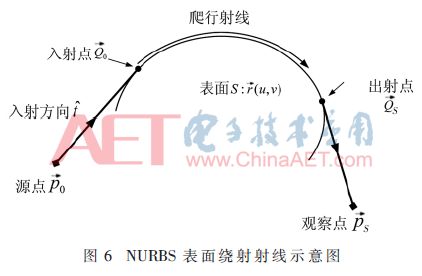
    根据这两个方程可以求解出NURBS曲面上大量的入射点与出射点。

2.2 基于自适应变步长欧拉法求解射线追踪GDE

    由于任意形状的表面上的爬行射线的路径满足GDE，因此可以将爬行射线的问题改为求解GDE的问题。一般来说，通过欧拉法求解GDE是一种简单快捷的方法。但是根据研究，在大多数情况下由于传统的欧拉法精度低，稳定性不好，导致求解效果不好。

    对于非线性问题，基本上需要步进控制校正程序。因此，本文中，为提高光线跟踪的准确性并确保效率，提出了自适应变步长欧拉方法来求解GDE。

    GDE方程如下：

 

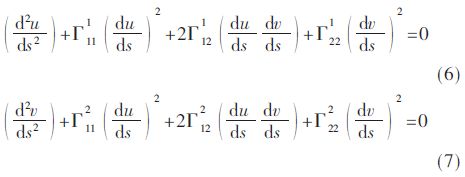
其中，h是两个相邻离散点之间的步长，并且确定它是非常重要的。ξ是形状因子（SF），用来自适应地控制每个离散步长。而ξ的值受制于对象的形状，关于ξ的更多细节将在2.3节中给出。

    在数值计算中，可以计算多个离散点(ui，vi)来表示爬行波，i=0，1，2…。因此，根据离散化，上式可以重写为：

    由式(13)可知，(ui+2，vi+2)能用(ui+1，vi+1)、(ui，vi)及ξi+1，i推导而出。必须计算出爬行射线最初的两个坐标(u0，v0)、(u1，v1)及ξ1，0，才能递推出整个爬行射线。

    可以通过方程(4)获得第一个点Q0(u0，v0)，然后由微分几何，第二个点可由Q0在u，v各自方向切向量之和近似表示，如图7所示。

    这里第二个点表示为：

    形状因子的一般表达式在2.3节中给出。根据表达式，可以确定得到ξ1，0。计算出(u0，v0)、(u1，v1)及ξ1，0后，(ui，vi)可以根据式(12)随着i的增加逐步迭代算出。

2.3 形状因子?孜的推导

    微分方程的精度与步长h有关，步长越小精度越高。然而，在迭代求解爬行波射线轨迹上的离散点的过程中，算法效率因离散点数的增加而减小，而且，离散点越多，累积误差越大，可能导致错误的结果。

    显然，为了逼近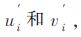

    但是在实际情况中，无法得知确定的(u(s)，v(s))表达式，所以导致离散点无法合理提取。于是本文提出用形状因子ξ来反映参数变化，用于确定离散步长。用ξ的离散值ξi+1，i来表示爬行射线相邻点参数变化率。ξi+1，i的表达式如下：

 

    设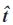

    对方程(17)中的变量s求微分，可得单位切向量：

3 数值算例与分析

    理论上可以在一些典型物体（如圆柱体、锥体）上计算爬行射线，因此，可以从这些对象的分析结果中验证所提出的方法是否有效。

3.1 圆柱体

    图9所示为圆柱表面（均匀网格）爬行波射线传播轨迹图。圆柱的半径为1 m，高为3 m。表1为爬行波寻迹结果，起始点为(1，0，0)。

 

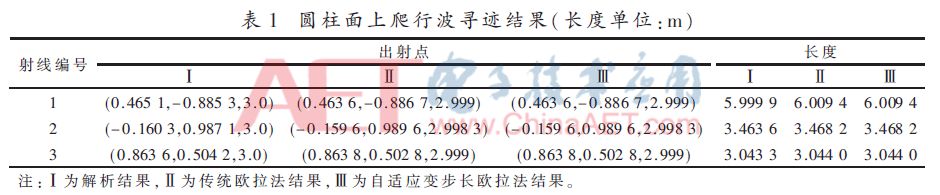
    从表1可知，采用自适应变步长欧拉法得到的数值结果与解析方法的结果吻合得非常好，由此可证明该寻迹算法正确性。

3.2 任意曲面目标

    图10所示为任意曲面表面（非均匀网格表面）爬行波射线传播轨迹图。根据微分几何知识，球面上的数值结果可以直接由理论值得到验证。表2为爬行波寻迹结果，起始点为(1.0，0.0，0.0)。

 

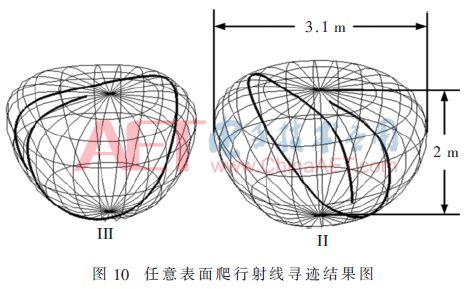
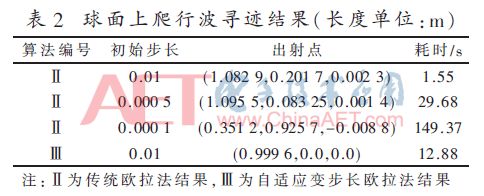
    如图10所示，提出的方法结果与理论结果吻合较好。从表2和图10可以看出，尽管随着离散步长的增加欧拉方法的误差减少了，但是耗时也增加了很多。更重要的是，如果离散步长继续增加下去，结果完全错误，这意味着欧拉方法不稳定。

4 结论

    对于任意形状NURBS目标表面爬行波射线轨迹寻迹，本文提出了基于自适应变步长欧拉法的快速有效的寻迹算法。为了验证该寻迹算法的正确性与有效性，给出了几个典型验证算例。相比于传统的欧拉法，自适应变步长欧拉法不仅继承了传统欧拉法的效率高的优势，而且该算法适用于任意的光滑曲面。