用两个日常的例子为我们讲解了决策树的原理

编者按：作为机器学习两大重要算法——随机森林和梯度树提升的基础，决策树是每位机器学习从业者都应该理解的概念。本文作者Brandon Rohrer用两个日常的例子为我们讲解了决策树的原理，过程清晰易读，适合入门学习。文末附有原文链接，感兴趣的读者可移步原文观看视频版本。以下是论智的编译。

决策树是我最喜欢的模型之一，它们非常简单但是很强大。事实上，Kaggle中大多数表现优秀的项目都是XGBoost和一些非常绝妙的特征工程的结合，XGBoost是决策树的一种变体。决策树背后的概念非常简洁明了，下面就用具体案例解释一下。

早上几点出门才能不迟到？

假设我们现在要创建一个数据集，记录每天上班离开家的时间以及能否准时到达公司。下图就记录了一些情况，可以看到大多数情况下，只要在8:15之前出门就能准时上班，在这之后就会经常迟到。

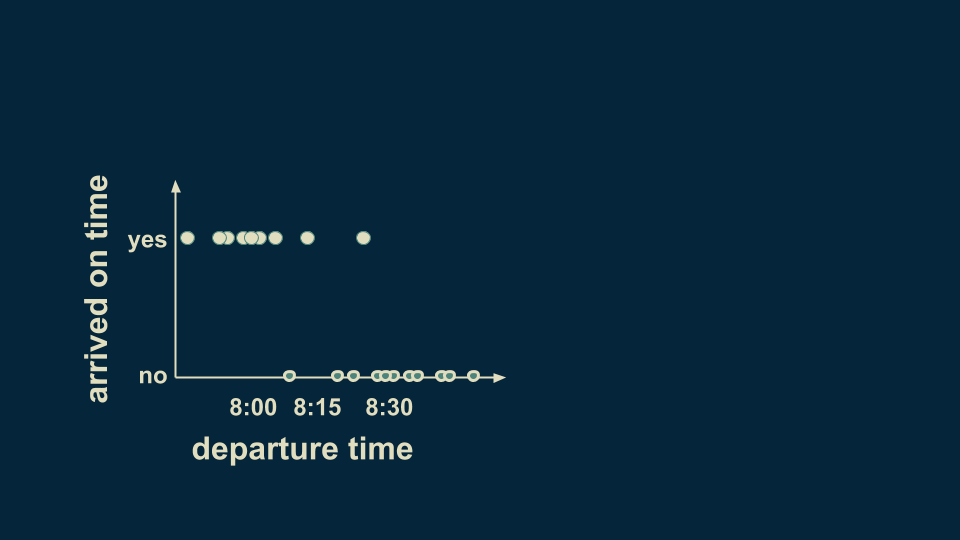
你可以在决策树中总结出这一情况。首先第一个分叉点可以问：“是否在8:15之前离开？”这里有两种回答：“是”或“否”。根据习惯我们将“是”放在左边，然后将数据分为两组，虽然有一些例外情况，但总体看来8:15是一个分水岭。如果在这之前出门，大概率不会迟到，反之亦然。

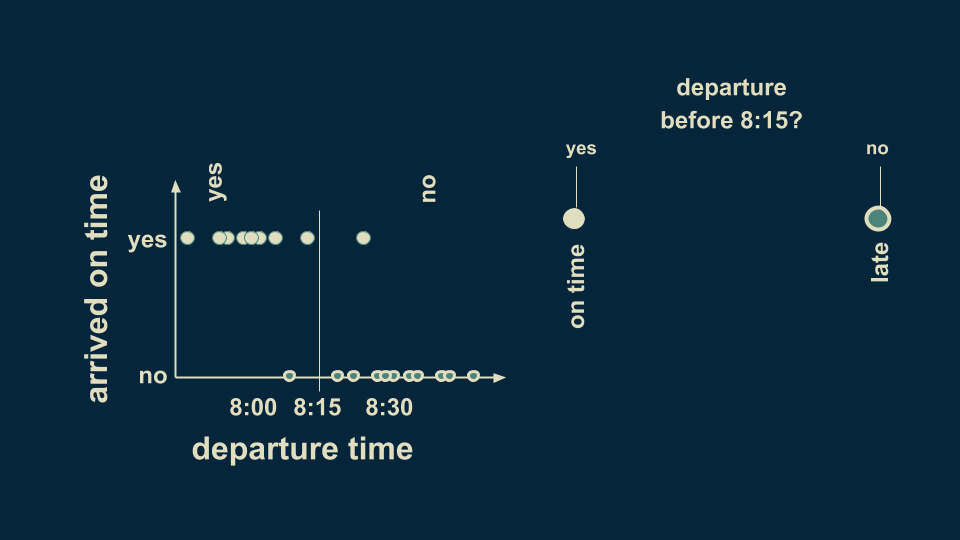
这就是最简单的决策树模型，只有一对选择分支。

接下来我们可以对这个模型进行微调，在两个分支上分别再进行分类，即加入8:00和8:30两个时间点，这样可以更全面地分析到达时间。下表显示，8:00之前出门绝对能准时到达，而8:00到8:15之间出门可能会准时到。而在8:15之后8:30之前几乎每次都会迟到，但也有可能不迟到。而8:30之后一定会迟到。

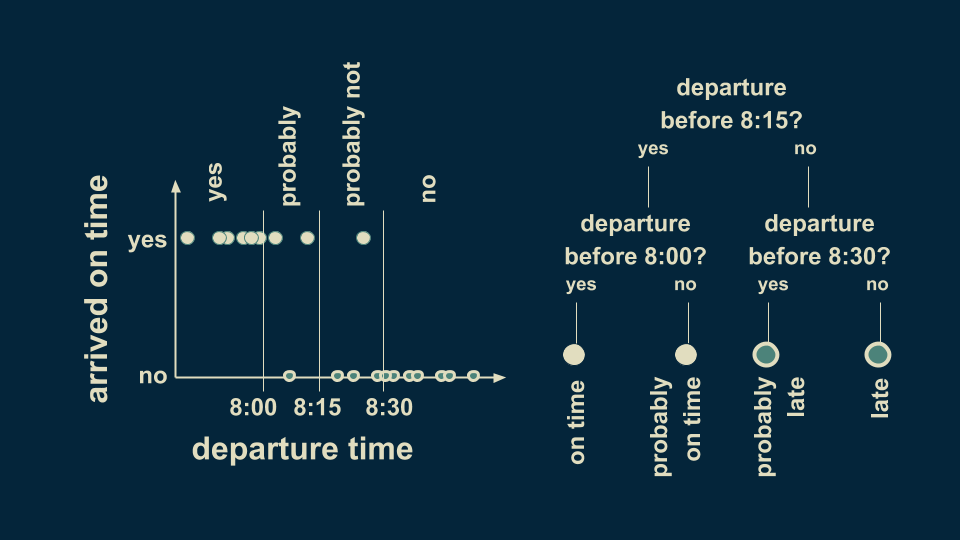
这样一来，决策树就变成了两层，你还可以根据自己的需要继续分层下去。大多数情况下，每个决策点只有两个分支。

上面的案例只有一个预测变量，以及一个类别目标变量。预测变量是“我们出门的时间”，目标变量是“是否准时上班”。由于只有两种明确的可能（是或不是），所以是分类的。有分类目标的决策树也被称为分类树。

我们可以将这一例子继续扩展，把它变成两个决策变量。将出门时间和工作日加入进去，将周一定为1，以此类推，周六为6，周日为7。数据显示，在周六和周日，绿色的点要更靠近左边一些。这说明在工作日，8:10出门也许足够了，但是周末可能会迟到。

为了在决策树中表示这一点，我们可以像之前一样，再在8:15时加上分界线，在这之后出发可能会迟到，但是在这之前却不好说，此前我们判断的是不会迟到，但现在看来这个推断不完全准确。

为了让我们更好地估计周末情况，我们可以进一步将8:15之前分为工作日和周末两种情况。工作日如果在8:15之前出发，那么一定不会迟到。但是周末如果在8:15之前出发，大多数情况会准时到达，但是也有例外。于是决策树可以如下图表示：

继续分类，将周末的8:15分继续分为8:00前和8:00后。如果8:00前出发，几乎每次都能准点到达，8:00至8:15之间出发，大部分都会迟到。现在我们有了一个二维决策树，将数据分成了四个不同区域。其中两个表示准点到达，另外两个表示迟到。

这是一个三层决策树，注意，并不是每个分支都需要继续细分下去（例如最右边的一支）。

现在我们可以分析一个具有连续目标变量的案例了。当模型对连续变量做出预测时，这也被称为回归树。我们已经解释了一维或二维的分类树了，接下来我们分析回归树。

你几点起床？

现在我们要加入某人的年龄以及他起床的时间。我们回归树模型的根节点就是对整个数据集的估计。在这种情况下，如果你不知道某人的年龄但还要估计他的起床时间，那么可能的时间是6:25，我们假设这是决策树的根节点。

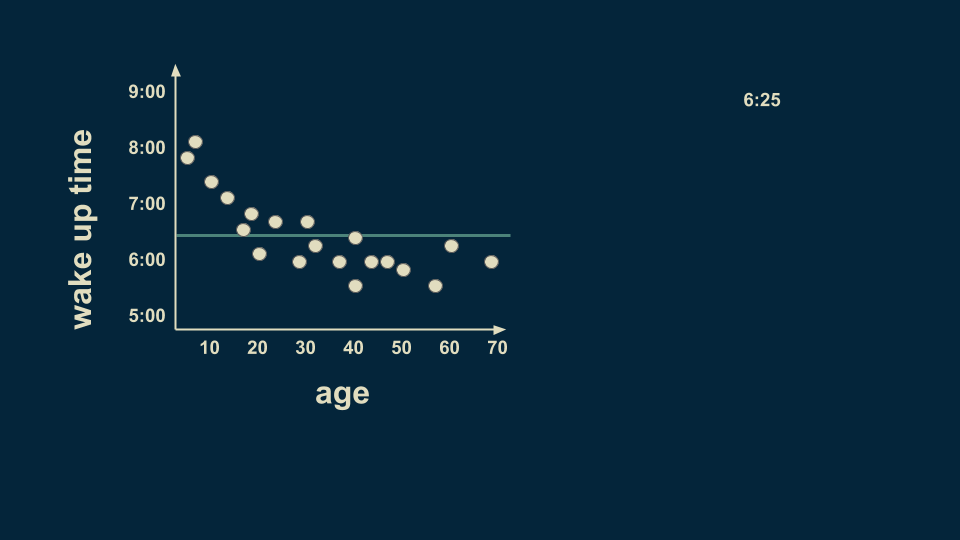
另一个关于年龄的分支我们定在25岁，经过数据收集，平均来说，25岁以下的人会在7:05起床，25岁以上的人会在6点钟起床。

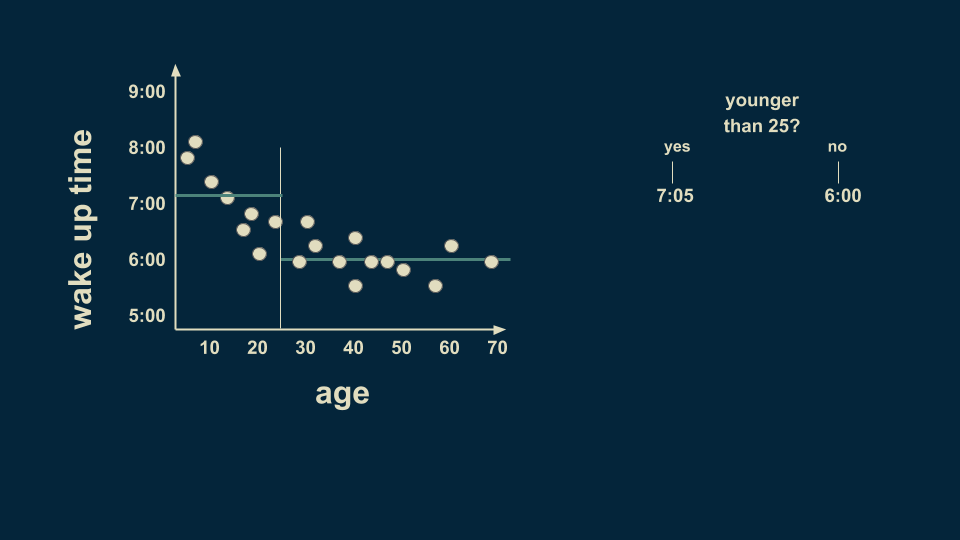
但是年轻人群体中也有变数，所以我们可以在进行分类。我们预计，12岁以下的人会在7:45起床，而12至25岁的人会在6:40起床。

25岁以上的人也可以进行细分。例如25至40岁的人平均在6:10起床，而40至70岁的人平均5:50起床。

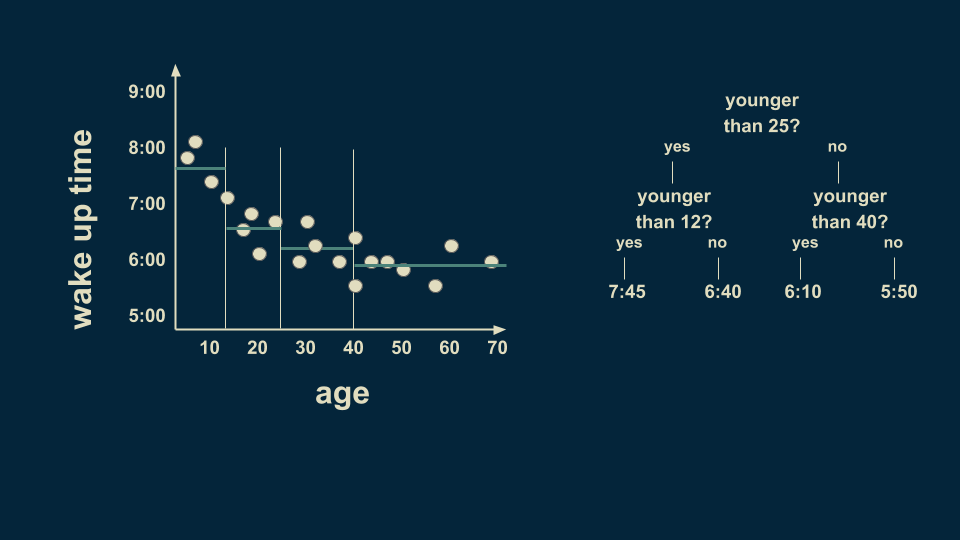
但是，年轻人群体中仍然有很多种情况，继续细分，以8岁为分界点，可以让预测的值更准确。我们也可以在40岁至70岁之间以58岁为分界点。注意，我们现在的某些“树叶”上只有一或两个数据点，这种情况很可能导致过度拟合，稍后我们会对其进行处理。

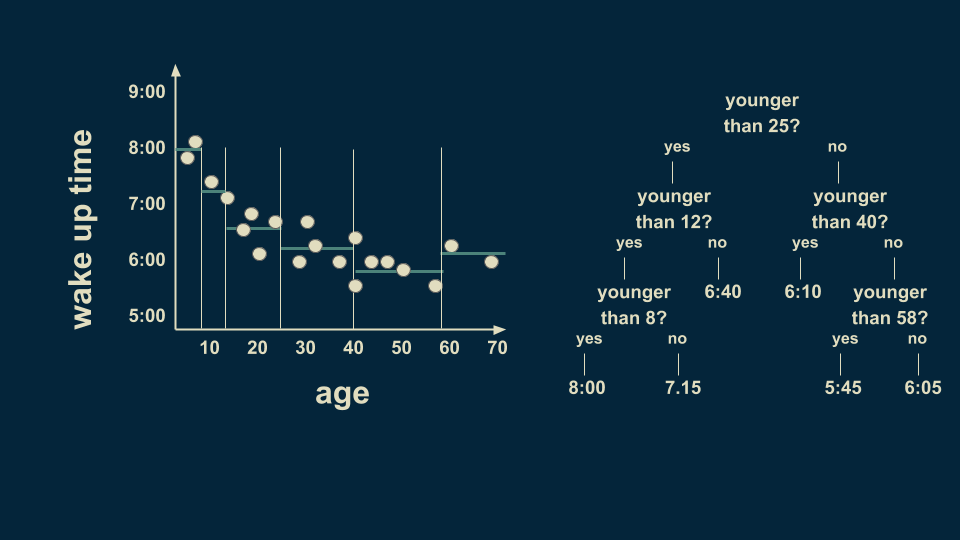
根据年龄，决策树能让我们做出多种判断。如果我要判断一名36岁的实验对象的起床时间，那么我可以从树的顶端开始。

他是否小于25岁？否，向右。低于40岁？是的，向左。最终估计的起床时间为6:10。

决策树的结构能让你将任何年龄的人分到各自的类别中，并且预测出他们的起床时间。

我们还可以将回归树模型扩展到有两个预测变量的形式。如果我们不仅考虑某人的年龄，还要考虑月份，那么我们会找到更加丰富的模式。目前北半球是夏季，昼长夜短，太阳日出时间较冬季更早。假设学生们没有课业压力（当然只是假设），他们的起床时间受太阳升起的影响，另一方面，成年人的起床时间就更加规律，只会随着季节变化进行轻微波动。另外，老年人在这个情况下会起的稍早。

我们创建的这个决策树和上一个很像。从根节点6:30开始（这里是用matplotlib进行的可视化）

之后我们寻找一个适合加入边界的地方，以35岁为分界线，35岁以下的人在7:06起床，35岁以下的人在6:12起床。

重复之前的过程，在年轻群体中细分时间，判断是否是9月中旬、是否是3月中旬。若在9月中旬之后，那么就判定为冬季，35岁以下的人起床时间估计为7:30，而夏季预计为6:56。

接着，我们可以在大于35岁的群体中继续以48岁为界线进行精确的分析。

我们同样还可以回过头，在35岁以下群体中分析18岁人群冬季的起床时间，如下图。18岁以下的人冬季在7:54起床，而18岁以上的人在6:48起床。

从这里，我们看到随着分支的增加，决策树模型的形状越来越接近原始数据的形状。同样，我们也会注意到决策树所区分的各个区域，颜色也越来越相近。

这一过程如果继续下去，模型就会不断接近数据原始形状，每个决策区域会变得越来越小，对数据的估计也会越来越准确。

如何处理过拟合

然而，决策树需要注意的一个重点是过度拟合。回到我们只有单一变量的回归树案例，即年龄对起床时间的影响中，假设我们继续细分年龄，直到每个类别中只有一两个数据。

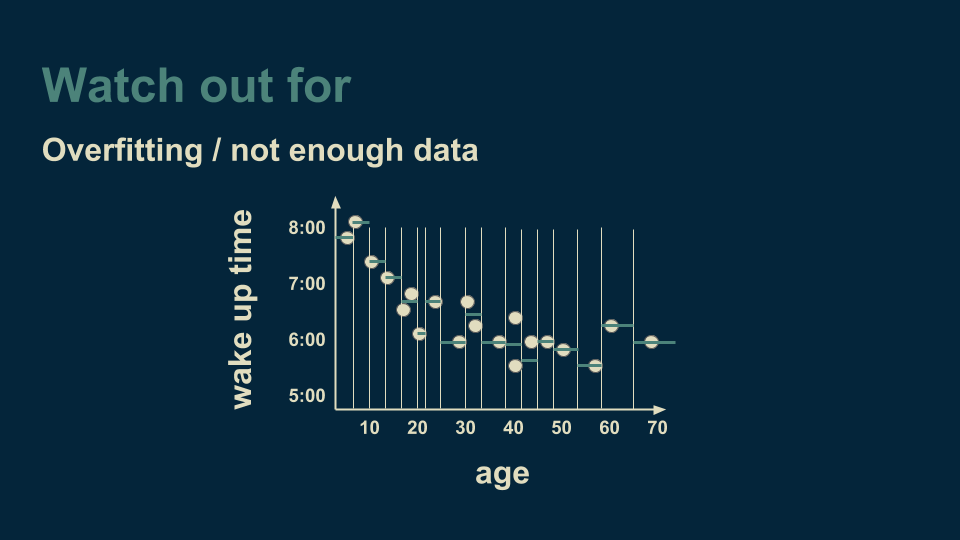
到了这时，决策树能非常好地解释并拟合数据，它不仅能掌握基本趋势，还能捕捉噪声。如果用该模型对新数据进行预测，那么训练数据中的噪声会让预测精确度降低。理想情况下，我们想让决策树捕捉趋势但不要夹杂噪声。要达到这一效果，比较有保障的方法就是在每片“树叶”上有多个数据，这样一来，噪声就会被平均掉。

另一种需要警惕的现象是变量过多的情况。我们一开始的回归树是一维的，后来加上了“月份”数据，成为了二维回归树。但是决策树不在乎有多少个维度，我们甚至可以加上地区纬度、某人锻炼量、身体的大数据或任何可能想到的变量。

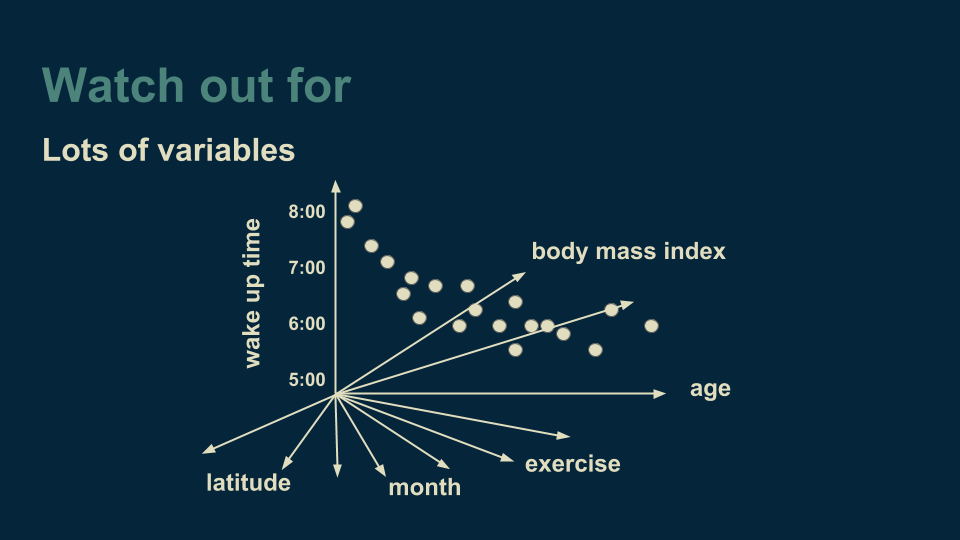
变量一多，接下来就要考虑细分哪些变量了。如果变量很多，就需要大量计算。同时我们加入的变量越多，所需要的数据就越多，所以处理起来要耗费大量精力。

当你相对数据进行必要解读时，决策树真的非常有用，它们很普遍，可以处理预测变量和目标变量之间非线性的关系。二次方程、指数关系、周期循环等等关系都能在决策树中表示，只要你有足够的数据支持。决策树同样可以发现不平滑的趋势，例如突然下降或上升，或者其他人工神经网络等模型的隐藏趋势。作为数据分析的工具，决策树的优势还是很明显的。