排序算法如何在机器学习技术中发挥重要作用

在机器学习中，支持向量机（SVM）算法是针对二分类任务设计的，可以分析数据，识别模式，用于分类和回归分析。训练算法构建一个模型，将新示例分配给一个类别或另一个类别，使其成为非概率二元线性分类器；使用核技术还可以有效地执行非线性分类。迄今为止线性核技术仍是文本分类的首选技术。

今天，人工智能头条将首先从支持向量机的基础理论知识入手，和大家探讨一个良好的排序算法如何在解决 SVM 问题过程中，在机器学习技术中发挥的重要作用。

▌前言

当前，机器学习(ML) 正在迅速成为现实社会中最重要的计算技术之一。作为人工智能(AI)的一个分支，这项技术适用于诸多领域，包括自然语言翻译和处理领域(如Siri 和Alexa)、医学研究，自动驾驶及商业战略发展等。一些令人眼花缭乱的算法正在被不断创造来解决ML 问题，并从数据流中学习模式以构建AI 的基础设施。

然而，有时候我们需要回头思考并分析一些基本算法是如何在这场机器学习革命中发挥作用及其所带来的影响。下面我就举一个非常重要的案例。

▌支持向量机

支持向量机(SVM) 是过去几十年发展中出现的最重要的机器学习技术之一。它的核心思想是给定一组训练样本，每个样本标记属于二分类中的一类，SVM 将构建一个用于对一个新的样本进行分类的模型，也就是说，它其实是一个非概率的二元线性分类器，广泛用于工业系统，文本分类，模式识别，生物ML 应用等。

SVM 的核心思想主要如下图所示，它的最终目标是将二维平面中的点分为红蓝两类，这可以通过在两组点集之间创建分类器边界(利用分类算法从带标记的数据中学习边界信息) 来实现。下图中展示了一些可能的分类器，它们都将正确地对数据点进行分类，但并非所有分类器都能使得分类后最接近边界的数据点具有相同的边距(距离)。从下图中我们可以看出，其中只有一个分类器能够最大化红色和蓝色点之间的距离，我们用实线表示该分类器而用虚线表示其他分类器。这种边距最大化的效用是尽可能地放大两个类别之间的距离，以便对新的点分类时分类器的泛化误差尽可能小。

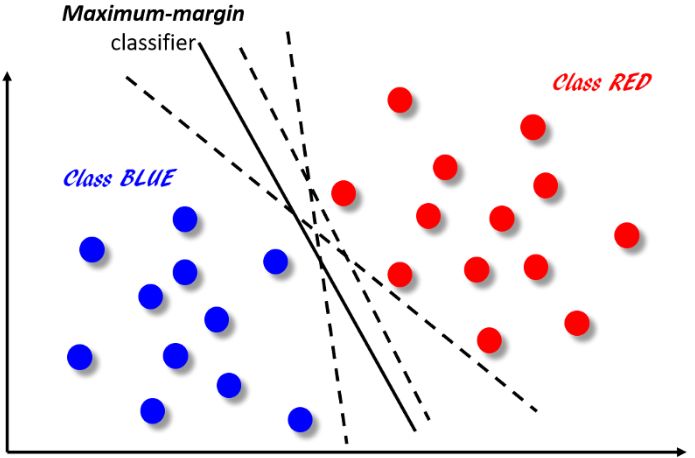
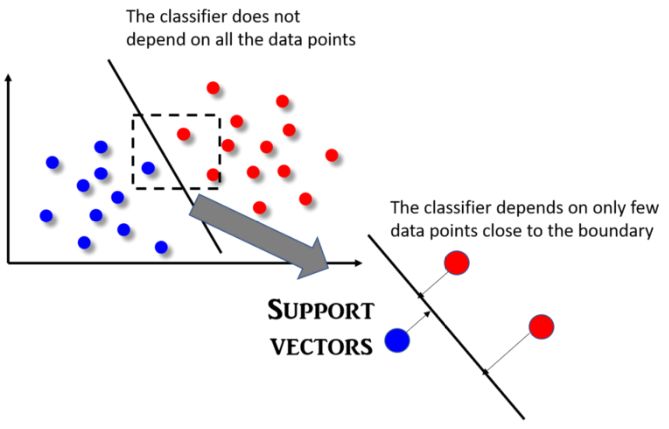
SVM 算法最明显的特征是分类器不依赖于所有数据点，这不同于依赖每个数据点特征并将其用于构造分类器边界函数的逻辑回归算法。实际上，SVM 分类器会依赖于一个非常小的子数据点集，这些数据点最接近边界，同时它们在超平面中的位置可以影响分类器边界线。由这些点构成的向量唯一地定义并支持分类器函数，因此我们把这种分类器称之为“支持向量机”，它的概念图解如下图所示。

这里，我们为大家准备了一个关于 SVM 的精彩视频教程。

▌关于SVM工作背后的几何解释：Convex Hull

SVM 算法背后的形式数学相当复杂，但从直观地我们可以理解为这是一种称为 Convex Hull 的特殊几何结构。

什么是Convex Hull 呢？形式上，在欧几里德平面（Euclidean plan）或欧几里德空间（Euclidean space）中的一组 X 点的凸包（convex hull）或凸壳（convex envelope）或闭包（convex closure），是包含 X 点的最小凸集。我们可以通过类比“橡皮筋”来更容易地理解这个概念。想象一下，橡皮筋在一组钉子（类比我们的感兴趣点）周围伸展。如果橡皮筋被释放，它会缠绕在钉子周围，从而形成一个紧密的边界，这是我们开始定义的集合。由此产生的形状就是凸包，我们可以通过那些由橡皮筋产生的边界钉子集来描述它，下面的图解将有助于更直观地感受这个概念。

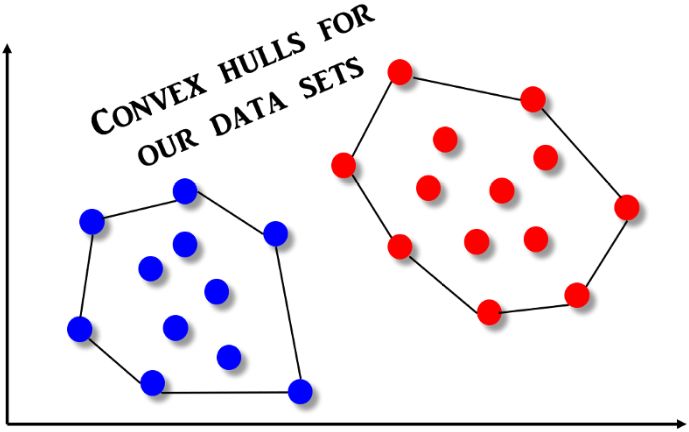
现在，我们可以很容易想象SVM 分类器只不过是一种线性分类器，它通过二分法将连接这些凸包的线一分为二。因此，确定SVM 分类器也就解决了找到一组点的凸包问题。

▌那么，如何确定凸包呢？

我们通过下面这个动画来说明这个问题！这里，我将展示用于确定一组点的凸包的Graham’s scan 算法。该算法能够沿着凸包的边界顺序，依次找到其所有的顶点，并通过堆栈的方法有效地检测和去除边界中的凹陷区域。

现在还有个问题是这种算法的效率如何，即Grahan’s scan 算法的时间复杂度是多少呢？

事实证明，Grahan’s scan 算法的时间复杂性取决于它用于寻找构成凸包的正确点集的基础排序算法。但是，一开始的排序算法又是什么呢？

Grahan’s scan 算法的基本思想来自凸包的两种特性：

只能通过逆时针转动来横穿凸包区域 

关于具有最低y 坐标的点p 而言，凸包的顶点将以极角递增的顺序出现。

首先，这些点以数组 points 的形式存储。因此，算法由定位的参考点开始，这是具有最低 y 坐标的点（在有捆绑关系(ties) 的情况下，我们通过选择具有最低 x 和 y坐标的点来解绑）。一旦我们找到参考点，我们可以将该点移动到数组 points 的开头，使其与数组中第一个点互换位置。

接着，利用剩余点相对于参考点的极角关系，我们对其进行排序。经过排序后，相对于参考点的极角最小点将位于数组的开始处，而具有最大的极角点将位于数组的末尾。

随着所有的点都被正确地排序，现在我们可以运行算法的主循环部分。当我们处理主数组中的点时，循环并将增长和缩小第二个列表。基本上，如果我们顺时针地旋转点，那么这些点将被推到堆栈上；反之，则如果我们以逆时针地方向，则拒绝并从堆栈弹出这些点。第二个列表一开始是个空列表，在算法结束时，构成凸边界的点将出现在此列表中。堆栈数据结构正用于此目的。

# Three points are a counter-clockwise turn if ccw > 0, clockwise if# ccw < 0, and colinear if ccw = 0 because ccw is a determinant that #gives twice the signed  area of the triangle formed by p1, p2, and #p3.function ccw(p1, p2, p3):    return (p2.x - p1.x)*(p3.y - p1.y) - (p2.y - p1.y)*(p3.x - p1.x)let N be number of pointslet points[N] be the array of pointsswap points[0] with the point with the lowest y-coordinate# This is the most time-consuming stepsort points by polar angle with points[0]let stack = NULLpush points[0] to stackpush points[1] to stackpush points[2] to stackfor i = 3 to N:    while ccw(next_to_top(stack), top(stack), points[i]) <= 0:        pop stack    push points[i] to stackend

因此，Graham’s scan 算法的时间复杂度取决于排序算法的效率。我们可以使用任何通用的排序算法，但对于时间复杂度为 O (n^2) 和 O (n.log(n)) 的算法而言（如下面的动画所示），它们之间的 Graham’s scan 算法的效率存在很大差异。

▌总结

在本文中，我们展示了简单排序算法在解决 SVM 问题过程中发挥的作用，以及它与广泛使用的机器学习技术之间的关系。虽然有许多基于离散优化的算法可以用来解决SVM问题，但在构建复杂的AI 学习模型方面，这种方法被视为是一种重要而基础高效的算法。