

以高通滤波器基础的快速协同设计方法详解
RF/无线
描述
滤波器是一种能从含有很宽频率的信号中选出所需要的部分,并将不需要部分衰减掉的电路,利用它来分开或组合不同的频率,如在放大器,混频器以及多路通信电路中等,总之,从超长波经微波到光波以上的所有电磁波段,都需要滤波器。有源模拟滤波器常用的设计方法是以插入衰减理论为基础的,称为插入衰减法或工作参数法,也称为综合法。此方法常包含4步:1)根据设计指标要求规定一个理想的衰减特性;2)用一个可实现的有理函数来逼近这个特性;3)用网络综合理论,把这个函数综合成一个实际的电路网络;4)利用仿真软件测试设计指标是否达到,并进一步完善设计。按照此流程设计的滤波器,其实际特性可以和预先规定的指标十分接近。根据网络综合的方法有许多可能的解,它们有不同的网络结构和不同的元件值。因此,根据各种准则,在涉及到成本、性能、灵敏度、方便性和工程技术鉴定等因素选择一个相对最佳的解,从许多可供选择的方案中选择一个方案也是设计的一个组成部分。
上述设计流程中的第2步即滤波器传递函数是设计中的关键部分,其设计时间的缩短将会大大提高整体设计的效率。获取传递函数的常用方法是由衰减指标和通带、阻带截止频率、逼近函数经手工计算或查表得到滤波器阶数和其传递函数中多项式系数或系统极点进而得到传递函数。但手工计算过程冗长且容易出错;可查的表格通常也只能列出阶数在10以内的传递函数多项式系数。就所查阅的文献显示,设计该类滤波器的方法众多,但很多文献是对阶数已知的低阶滤波器(如二阶)进行分析和改进设计,没有给出由详细指标要求到系统传递函数求取再到电路综合实现的全过程,即便给出综合过程的也是以手工计算或查表来获取滤波器阶数及传递函数。在现阶段计算机数值处理运算速度快和精度高的条件下,完全可以通过计算机处理繁琐、冗长的手工计算过程,特别是对阶数较高无法通过查表直接设计的滤波器。有源模拟滤波器的快速协同设计方法将滤波器参数的求取由计算机程序来完成,即在MATLAB程序中给入通带或阻带衰减指标要求和边界频率获得其原型滤波器阶数n和截止频率Ωc,利用这两个关键参数进一步求得具体的滤波器如高通、带通等滤波器传递函数H(S),也可经程序求得以双二次函数形式表达的滤波器传递函数的二阶级联基本形式,以此为基础再进行电路综合,缩短了高阶滤波器的设计时间,最后由EDA软件在电路模型基础上验证设计方案是否满足设计指标要求,并作进一步的完善和改进,由于篇幅有限,见文献。下面将以高通滤波器为例,介绍此快速协同设计方法。
1 基于频率变换的滤波器传递函数设计
1.1 频率变换流程
有源模拟滤波器设计流程是由低通滤波器开始经频带变换得到其他类型的滤波器,首先利用实频率域的频率变换方法,将高通、带通、带阻的技术指标转换为对低通的技术要求,然后按要求设计低通的转移函数,再利用复频率域中的频率变换方法,将设计好的低通转移函数转换为高通,带通和带阻的转移函数。如图1所示。
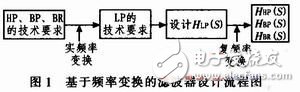
1.2 滤波器设计手工计算示例
以实现一个切比雪夫(Chebyshev)高通滤波器为例,其电压衰减指标为:通带的最大衰减αmax为0.1 dB,阻带内最小衰减αmin为20 dB;通带边界频率为ωp=1 250(rad/s)(fp=199 Hz),阻带边界频率为ωs=500(rad/s)(fs=79.6 Hz)。按上述要求经手工计算得到归一化复频率下的低通传递函数HLP(S)为:
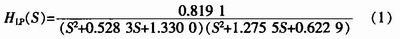
对HLP(S)施行复频率变换,利用复频率变换公式SLP=1/SHP,得高通(归一化复频率)的传递函数:
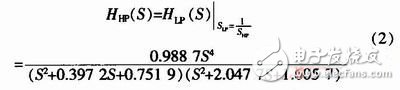
对归一化复频率的高通传递函数进行频率的去归一化,从而得出实际频率下的高通传递函数。为此应将HHP(S)中的S以s/ωp取代。从而得到实际的高通传递函数H(s)为:
上面只给出了手工计算过程中的几个关键结果,略去了冗长的手工计算过程,即便是通过查表进行计算,也只能对阶数有限的滤波器减少设计时间,下面将用程序实现滤波器传递函数的快速设计,此法对低阶或高阶的滤波器设计均适用。
2 滤波器的快速设计方法
对文1.2中切比雪夫高通滤波器的传递函数在MATLAB下重新进行求解,并和手工计算结果进行比较,给出两种在MATLAB环境下的实现方法。
2.1 滤波器设计的MATLAB实现
将图1设计流程程序化,首先将对高通滤波器的指标要求利用实频率变换转为对低通滤波器的指标要求,进而在MATLAB环境中求取低通滤波器传递函数即低通滤波器原型;再利用MATLAB在s域中的频带变换将低通原型变换为符合指标要求的高通滤波器二阶级联传递函数形式,为下一步的电路综合做好准备,具体程序如下:

如果少了这个变元,MATLAB会直接设计数字滤波器。该函数返回值为满足技术指标要求的滤波器的最小阶数n和滤波器3 dB带宽的截止频率OmegaC。对切比雪夫I滤波器该函数选OmegaC为OmegaP的大小。

GO=8.190 3e-001其结果与手工计算结果式(1)比较,可见精度很高。
以下为频率去归一化后高通滤波器传递函数二阶级联形式系数输出:

以上与手工计算结果式(3)比较,可见精度也很高。在该程序中,tf2sos()和lp2hp()是关键的函数,它们分别完成了传递函数形式到级联结构的转换和低通原型滤波器(归一化)到高通滤波器(去归一化)的设计。
2.2 滤波器快速设计的MATLAB实现
CHEBY1切比雪夫滤波器完全设计函数将式(1)中涉及到的实频率和复频率变换都封装成了函数,因此利用该函数程序实现起来更为直观和快捷,程序语句大为减少,具体程序如下:

可以看到,该结果也和手工计算结果式(3)相差无几而且较前一程序大为简化,只用了4条语句即可实现。故采用完全设计函数将使设计效率更高。
如前所述,一个高阶滤波器的传递函数可以表示为多个双二次函数乘积形式如(3)式,故高阶滤波器电路结构就是各双二次函数对应电路的级联,现利用负反馈双二次电路实现前面的切比雪夫高通滤波器,如图2所示。
3 EDA仿真实验结果
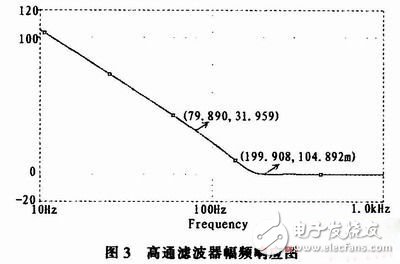
由于EDA的仿真结果更接近于真实电路的测试结果,是一种电路硬件级的仿真,利用EDA工具对实现的高阶滤波器电路进行性能测试仿真,来验证设计结果是否达到技术指标的要求,可以很好地协助MATLAB完成电路实现可行性的论证。在Pspice中进行AC分析后,启动图形后处理程序Probe并添加要显示的波形函数,如图3所示。从频率响应曲线可以看出,在阻带边界频率ωs=500(rad/s)、(fs=80 Hz)和在通带边界频率ωp=1 250(rad/s)、(fp=200 Hz)处的电压衰减值均可以满足滤波器指标设计要求。此后还可利用EDA软件中的容差分析功能为元器件进一步选择合适的容差,提高设计的成品率和稳定性。
4 结束语
提出了不同于传统有源模拟滤波器的设计方法,即不通过手工计算或查表而通过MATLAB程序实现滤波器传递函数或其二阶级联传递函数,之后再协同EDA软件在电路器件模型上进一步验证方案是否合理和可行的方法。由于在MATLAB程序中可方便地调用滤波器原型设计函数及频率变换函数,通过选择合适的设计参数,便可快速得到正确的设计结果。EDA环境下的仿真结果进一步验证设计结果是否具有可行性并做进一步的完善。实验结果证明,该方法大大提高了滤波器电路的设计效率,使得设计人员在设计时方向更加明确,硬件成本大大降低,产品开发周期大大缩短。但该法需要设计人员事先对所设计的滤波器原理及特性有较全面的了解,这样才能在MATLAB程序中灵活的调用各种函数,做到游刃有余。
- 相关推荐
- 热点推荐
- �
-
高通滤波器和低通滤波器判别方法2024-07-15 2841
-
高通滤波器、低通滤波器、带通滤波器怎样测幅频特性?2024-03-28 7870
-
如何判断高通滤波器和低通滤波器2023-06-26 6167
-
高通滤波器的原理_高通滤波器参数设计2023-02-25 12230
-
低通滤波器与高通滤波器有什么不同2023-02-17 15640
-
高通滤波器的幅频特性_高通滤波器的截止频率2023-02-16 14354
-
二阶有源高通滤波器原理详解2022-11-18 5100
-
高通滤波器和低通滤波器的区别是什么2020-08-12 43408
-
悬置线高通滤波器的设计原理和方法2020-07-17 1566
-
高通滤波器的定义、应用和实现方法2017-11-23 10646
-
VCVS高通滤波器电路原理及函数2010-05-23 5727
-
实用高通滤波器电路2009-12-07 4958
-
有源高通滤波器2009-09-16 3055
-
高通滤波器设计2008-12-01 3892
全部0条评论

快来发表一下你的评论吧 !

