激活函数中sigmoid、ReLU等函数的一些性质

本文主要是回答激活函数的使用

我们认识的激活函数中sigmoid、ReLU等，今天就是要讲解一下这些函数的一些性质

激活函数通常有一些性质：

非线性：当激活函数是线性的时候，一个两层的神经网络就可以基本逼近所有的函数，但是，如果激活函数是恒等激活函数的时候，就不满足这个性质了，而且如果MLP使用的是恒等激活函数，那么其实整个网络跟单层神经网络是等价的

可微性：当优化方法是基于梯度的时候，这个性质是必须的

单调性：当激活函数是单调的时候，这个性质是必须的

f(x)≈x： 当激活函数满足这个性质的时候，如果参数的初始化是random的很小的值，那么神经网络的训练将会很高效；如果不满足这个性质，那么就需要很用心的去设置初始值

输出值的范围：当激活函数输出值是有限的时候，基于梯度的优化方法会更加稳定，因为特征的表示，当激活函数的输出是无限的时候，模型训练会更加的高效，不过在这种情况很小，一般需要一个更小的学习率

Sigmoid函数

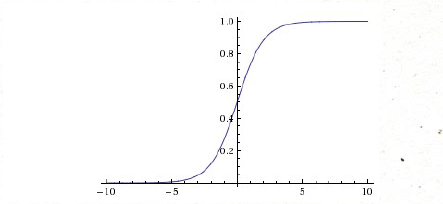
Sigmoid是常用的激活函数，它的数学形式是这样，

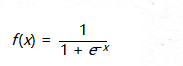
当如果是非常大的负数或者正数的时候，梯度非常小，接近为0，如果你的初始值是很大的话，大部分神经元都出在饱和的情况，会导致很难学习

还有就是Sigmoid的输出，不是均值为0为的平均数，如果数据进入神经元的时候是正的(e.g. x>0 elementwise in f=wTx+b)，那么 w 计算出的梯度也会始终都是正的。 

当然了，如果你是按batch去训练，那么那个batch可能得到不同的信号，所以这个问题还是可以缓解一下的。因此，非0均值这个问题虽然会产生一些不好的影响

tanh

和Sigmoid函数很像，不同的是均值为0，实际上是Sigmoid的变形

数学形式

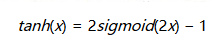
与Sigmoid不同的是，tanh是均值为0

ReLU

今年来，ReLU貌似用的很多

数学形式

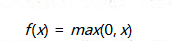
ReLU的优点

相比较其他的，ReLU的收敛速度会比其他的方法收敛速度快的多

ReLU只需要一个阈值就可以得到激活值，而不用去算一大堆复杂的运算

也有一个很不好的缺点：就是当非常大的梯度流过一个 ReLU 神经元，更新过参数之后，这个神经元再也不会对任何数据有激活现象了，所以我们在训练的时候都需要设置一个比较合适的较小的学习率

Leaky-ReLU、P-ReLU、R-ReLU

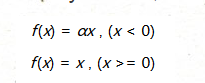
数学形式

f(x)=x，(x>=0)

这里的 α 是一个很小的常数。这样，即修正了数据分布，又保留了一些负轴的值，使得负轴信息不会全部丢失

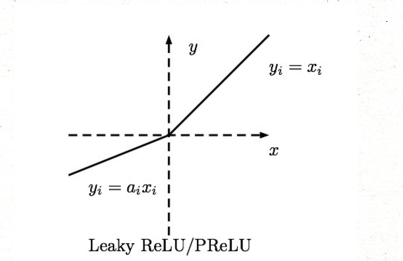
自己在写神经网络算法的时候还没尝试过这个激活函数，有兴趣的同学可以试试效果

对于 Leaky ReLU 中的α，通常都是通过先验知识人工赋值的。 

然而可以观察到，损失函数对α的导数我们是可以求得的，可不可以将它作为一个参数进行训练呢？ 

不仅可以训练，而且效果更好。

如何去选择

目前业界人都比较流行ReLU，