什么是神经算术逻辑单元？

众所周知，神经网络可以学习如何表示和处理数字式信息，但是如果在训练当中遇到超出可接受的数值范围，它归纳信息的能力很难保持在一个较好的水平。为了推广更加系统化的数值外推，我们提出了一种新的架构，它将数字式信息表示为线性激活函数，使用原始算术运算符进行运算，并由学习门控制。我们将此模块称为神经算术逻辑单元(NALU) ，类似于传统处理器中的算术逻辑单元。实验表明，增强的NALU 神经网络可以学习时间追踪，使用算术对数字式图像进行处理，将数字式信息转为实值标量，执行计算机代码以及获取图像中的目标个数。与传统的架构相比，我们在训练过程中不管在数值范围内还是外都可以更好的泛化，并且外推经常能超出训练数值范围的几个数量级之外。

▌简介

对数值表示和处理的能力在许多物种中普遍可见，这表明基本的定量推理是智力的一个组成部分。虽然神经网络可以在给定适当的学习信号的情况下成功地表示和处理数值量，但它们的学习行为缺乏系统的泛化。具体而言，当测试阶段的数值超出了训练阶段的数值范围，即使目标函数很简单也会导致出错。这表明学习行为的特点是记忆而不是系统抽象。

在本文中，我们设计了一个偏向于学习系统数值计算的新模块，该模块可以与标准的神经网络体系结构结合使用。我们的策略是将数值表示为无非线性的单个神经元，其中这些单值神经元采用的是类似于加减乘除的运算符来表示，运算符由参数来控制。

神经网络中的数值外推失效

为了说明标准网络中的系统性失效，我们展示了各种MLPs 在学习标量恒等函数的表现。图1表明即使采用简单的框架，所有非线性函数都无法学习到超出训练范围外的数量表示。

图1 MLPs 在学习标量恒等函数时的表现

▌神经累加器和神经算术逻辑单元

本文，我们提出了两种能够学习以系统的方式去表示和处理数字式信息的模型。第一种模型有支持对积累量进行累加的能力，这是线性外推的理想偏置项。该模型构成了第二个模型的基础，即支持乘法外推。此模型还阐述了如何将任意算术函数的偏置项有效地融合到端到端模型中。

第一个模型是神经累加器(NAC)，它是线性(仿射) 层的一种特殊应用，其变换矩阵W 只由-1,0和1组成。也就是说，它的输出是输入向量中行的加减算法，这也能够预防层在将输入映射到输出时改变数字的表示比例。

由于硬性的约束W 矩阵中的每个元素都为{-1,0,0}，这使得模型在学习中变得更加困难。为此我们提出了一种W 在无参数约束条件下的连续可微分参数化方法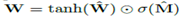： 。该方法给梯度下降学习带来了很大的方便，同时产生一个元素在[-1,1] 并且趋向于-1，0或1的矩阵。图2描述了一个神经算术逻辑单元(NALU)，它可以学习两个子单元间的加权和，一个能够进行加减运算，另一个则可以执行乘除以及幂运算，如 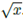。更重要的优点是，其能够展示如何在门控的子操作中扩展NAC，从而增强了新类型数值函数的端到端学习。

图2 (a) 神经累加器 (b)神经算术逻辑单元

图2中，NAC 是输入的一次线性变换，变换矩阵是tanh(W) 和 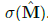元素的乘积。NALU 使用两个带有固定系数的NACs 来进行加减运算(图2中较小的紫色单元) 以及乘除运算(图2中较大的紫色单元)，并由门(图2中橙色的单元)来控制。

▌实验

我们跨域各种任务领域 (图像、文本、代码等)，学习信号 (监督和强化学习)，结构 (前馈和循环) 进行实验，结果表明我们提出的模型可以学习到数据中潜在数值性质的表示函数，并推广到比训练阶段的数值大几个数量级的数值。相比于线性层我们的模块有更小的计算偏差。在一个具体实例中，我们的模型超过了目前最先进的图像计数网络，值得一提的是，我们所做的修改仅是用我们的模型替换了其最后一个线性层。

简单的函数学习任务

在这些初始合成实验中，我们展示了NAC 和NALU 在学习选择相关输入并应用不同算术函数的能力。其中测试任务分为两类：第一类为静态任务，即以单个向量一次性输入；第二类是循环任务，即输入按时间顺序来呈现。通过最小化平方损失来端到端地训练模型，模型的性能评估由两个部分组成：训练范围内(插值) 的留存值和训练范围外(外推) 的值。表1表明了几种标准体系结构在插值情况下成功完成任务，但在进行外推时都没有成功。而不管是在插值还是外推上，NAC 都成功地建立加法和减法模型，NALU 在乘法运算上也获得成功。

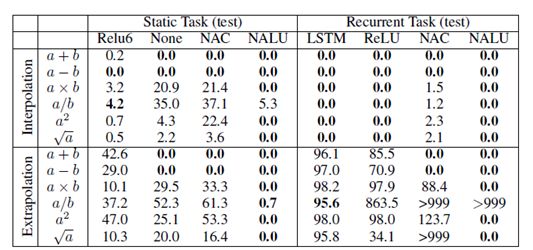
表 1 静态和循环任务的插值和外推误差率

MNIST 计数和算术任务

在这项任务中，我们给模型10个随机选择的MNIST 数字，要求模型输出观察到的数值和每种类型的图像数量，在MNIST 数字加法任务中，模型还必须学会计算所观察到的数字之和。在插值(长度为10) 和外推(长度为100和长度为1000) 任务上测试模型的计数和算术的性能。表2表明标准体系结构在插值任务上成功，但在外推任务上失败。但是NAC 和NALU 都能很好地完成插值和外推任务。

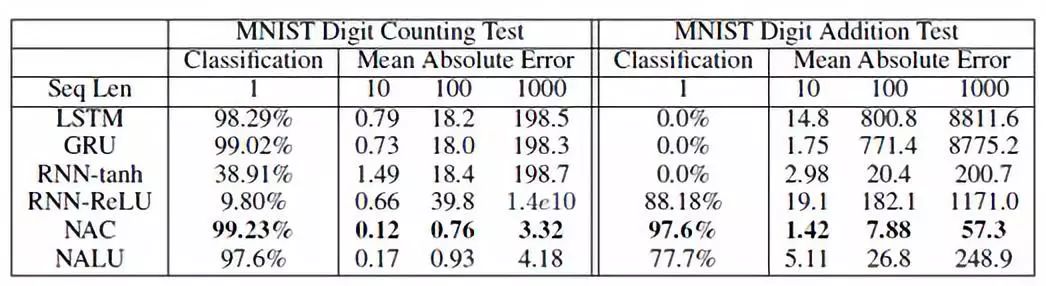
表2 长度为1，100，1000的序列的 MNIST 计数和加法任务的准确度

语言到数字的翻译任务

为了测试数字词语的表示是否是以系统的形式来学习，我们设计了一个新的翻译任务：将文本数字表达式(例如五百一十五) 转换为标量表示(515)。训练和测试的数字范围在0到1000之间，其中训练集、验证集和测试集的示例分别为169、200和631。在该数据集上训练的所有网络都以embedding 层开始，通过LSTM 进行编码，最后接一个NAC 或NALU。表3表明了LSTM + NAC 在训练和测试集上都表现不佳。LSTM + NALU 可以大幅度地实现最佳的泛化性能，这说明乘数对于此任务来说非常重要。这里还给出了一个NALU 测试的例子如图3所示。

表3 将数字串转换为标量的平均绝对误差(MSE) 比较

图3  NALU 的预测样例

程序评估

程序评估部分我们考虑两个方面：第一个为简单地添加两个大整数，第二个为包含若干个操作(条件声明、加和减)。此次评估专注于外推部分即：网络是否可以学习一种推广到更大数值范围的解决方案。用[0,100) 范围内的两位数整数来训练，并用三位或四位的随机整数来评估。图4比较了四种不同模型(UGRNN、LSTM、DNC 和NALU) 的评估结果，其中只有NALU 是能够推广到更大的数字。我们可以看到即使域增加了两个数量级，外推效果也是较为稳定。

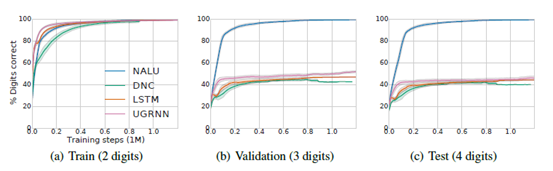
图4 简单的程序评估，外推到更大的值

学习在网格世界环境中追踪时间

到目前为止，在所有实验中，我们训练的模型已经可以进行数值预测了。然而，正如引言部分所说，系统化的数值推算似乎是各种智能行为的基础。因此，我们进行了一项任务，测试NAC 能否被RL-trained 智能体“内部”使用。

如图5所示，该任务中，每一帧都是从初始值开始(t=0)，红色的目标随机定位于5*5的网络世界方格中。每个时间步中，智能体接收一个56*56像素网格以表示整个网格世界环境状态，并且必须从{上移，下移，左移，右移，忽略} 选择其中的一个操作。测试开始前，智能体还会接收一个数字(整数) 指令T ,用来传达代理到底目的地的确切时间。

达到最大帧时，奖励m，智能体必须选择操作并四处移动。第一次移动至红色区域时就是t=T 的时候，当智能体到达红色区域或者时间结束时(t=L) 训练结束。

图5网格世界环境中时间追踪任务

MNIST 奇偶校验预测任务和消融研究

在我们的最后一项任务：MNIST 奇偶校验中，输入和输出都不是直接用数字提供的，而是隐式地对数字量进行推理。在这个实验中，NAC 或其变体取代了由Segui 等人提出的模型中的最后一个线性层。我们系统地研究了每个约束的重要性。表4总结了变体模型的性能，我们可以看到去除偏置项和运用非线性权重的方法显著提高了端到端模型的准确性，NAC 将先前最佳结果的误差减少了54%。

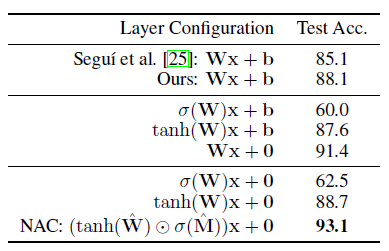
表4 关于MNIST 奇偶校验任务的affine 层和NAC 之间的消融研究

▌结论

目前，神经网络中数值模拟方法还不够完善，因为数值表示方法不能够对其训练观察到的数值范围外对信息进行较好的概括。本文，我们已经展示了NAC 与NALU是如何解这两个不足之处，它改善了数值表示方法以及数值范围外的函数。然而，NAC 或NALU 不太可能很完美的解决每一个任务。但它们可以被作为解决创建模型时目标函数存在偏置项的一种通用策略。该策略是由我们提出的单元神经数值表示方式实现的，它允许将任意(可微) 数值函数添加到模块中，并通过学习门进行控制。