SOA增益饱和特性仿真分析

引言

为了更好的理解SOA的特性，见合八方近期将会发布【SOA仿真】系列文章。

SOA的仿真，通常离不开载流子速率方程、传输方程、以及增益方程这三大方程，本文根据增益方程分析行波半导体光放大器TW-SOA的增益饱和特性。

关键词

半导体光放大器SOA、增益、小信号增益、增益饱和、仿真

1.增益方程

对行波半导体光放大器，示意图如下（图1）。

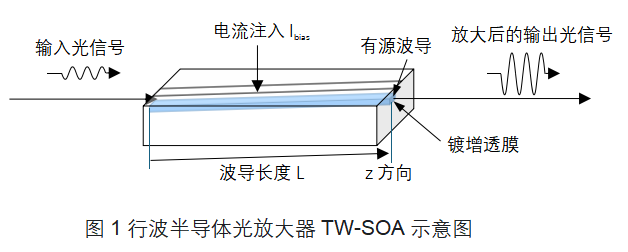
当光和偏置电流注入半导体光放大器时，SOA的有源区的增益会发生变化，放大器增益G(线性)可通过以下公式计算得出，对公式推导感兴趣的详见附录或文献[1]：

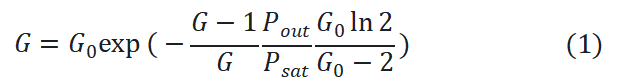
其中G0为增益峰值波长处的小信号增益（对某个特定偏置电流，该值为常数），Pout为输出光功率，Psat为饱和光功率（同样的，对某个特定偏置电流，其也是常数），公式中均为线性单位。

2.仿真

可以看出，公式1是指数方程，因此可采用迭代法求解，具体如下：

第一步：设置参数

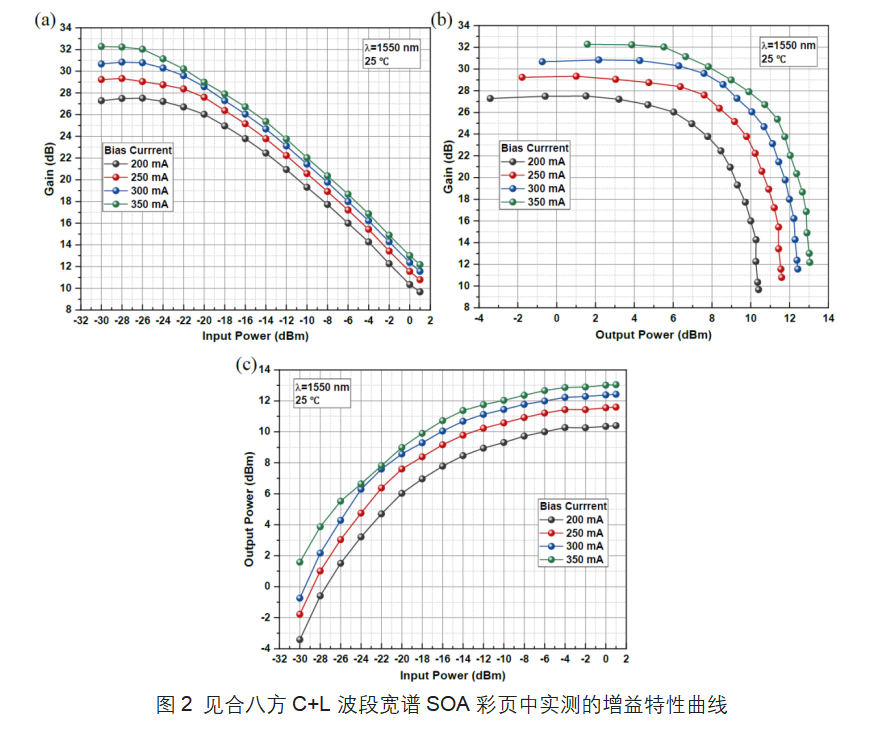
我们以见合八方C+L波段宽谱半导体光放大器（型号为JSA-BT5615G25）为例进行仿真，以验证仿真效果。根据其彩页中的数据设定Psat和G0，如图2所示（半导体光放大器SOA-天津见合八方-产品系列）
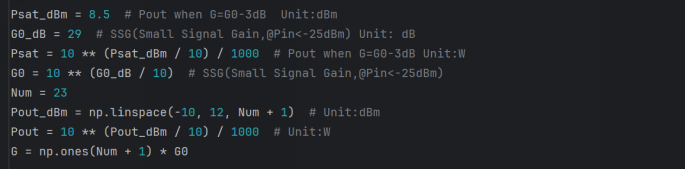
，在这里，我们选取Ibias=250mA时的数据，G0(dB)≈29dB，Psat_out(dBm)≈8.5dBm，Pout(dBm)设定取值范围-10dBm~12dBm。为通过公式1进行计算，我们将所有对数参数转换为线性值。

Python代码：

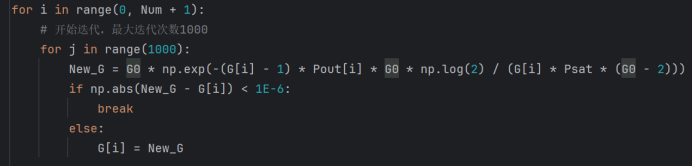
第二步：迭代求解增益方程

根据公式1给出的增益方程，针对不同的Pout取值，求解对应的G。

1.设置G的初始值为G0；

2.将G代入增益方程，求得新的New_G值；

3.比较New_G和G值，判断是否收敛，本仿真采用判决方法为|New_G-G|<1E-6；

4.如收敛则中止迭代，否则将G=New_G，重复步骤2。

Python代码：

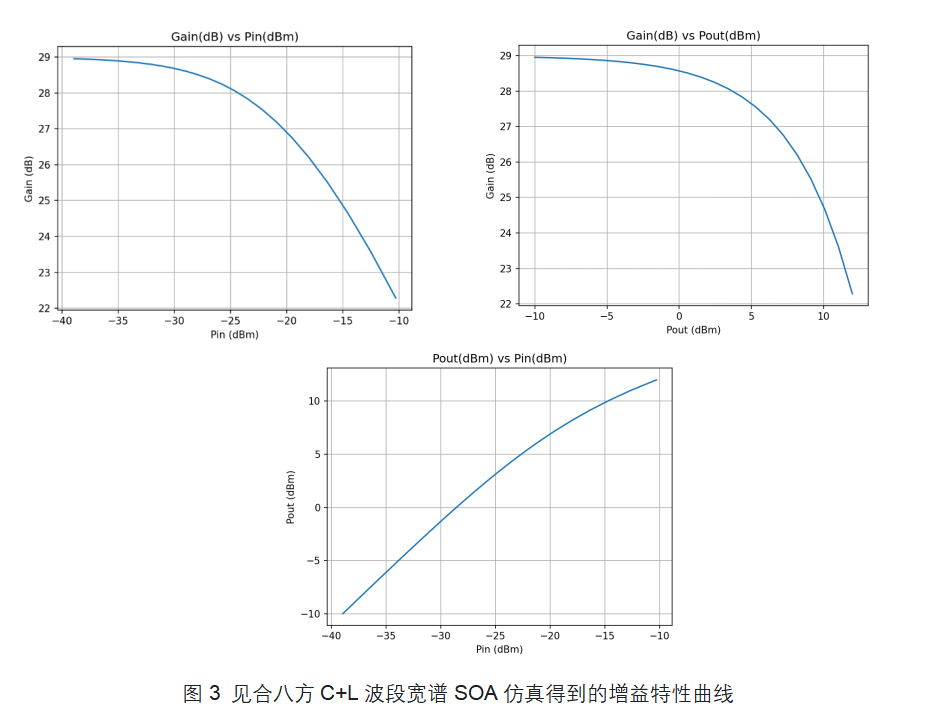
第三步：绘制仿真增益曲线

将所有计算结果重新转换为我们习惯的对数坐标，绘制增益曲线（图3）可以发现，与图2中的实测增益曲线相比，曲线重合度较高，并观察到了增益饱和特性（文献[2]）。

Python代码：

3.结果

由仿真结果可知，在半导体光放大器达到饱和状态之前，输出功率与输入功率呈线性增长关系；当半导体光放大器达到饱和状态后，有源区的载流子会逐渐耗尽，进而导致放大器增益下降。

本文对SOA增益饱和特性进行了初步仿真，后续我们还会对增益相关特性做进一步仿真。

附录.增益方程推导

增益方程的公式推导主要参考文献[1]，具体如下：

根据增益G的定义，有如下公式：

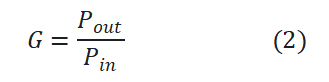
其中Pin和Pout分别是SOA的输入和输出光功率。

小信号输入时：

在小输入信号（Pin较小时），有下面公式：

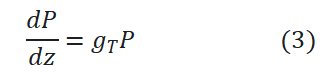
其中gT为净增益系数，单位为m-1，代表波导单位长度的放大倍数。由公式3可得到：

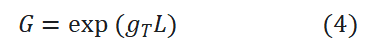
其中G为SOA的总增益，L为有源区波导总长度。

饱和输入时：

当Pin较大时，此时载流子大量消耗，进而导致增益降低，增益饱和，此时公式3修正为：

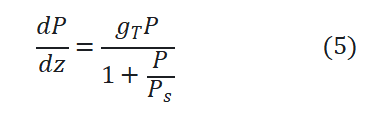
其中Ps是一个与饱和光功率Psat相关的参数（见后面的公式），由公式5可得到：

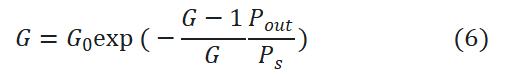
其中G0是最大增益（增益峰值波长处的小信号增益）。我们知道饱和输出光功率Psat_out的定义是当增益降低为小信号增益的一半时G=G0/2（如以对数来衡量时，对应降低3dB）的输出光功率，代入公式6得到：

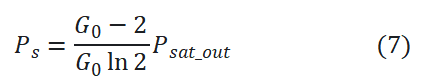
将公式7带入公式6，可得到增益方程（公式1）。

参考文献

[1] Niloy K. Dutta and Qiang Wang, “Semiconductor Optical Amplifiers,” Hackensacks, NJ: World Scientific Publishing Company, 2006.

[2] 王光全，沈世奎，王伟，曾志超等，“半导体光放大器SOA技术与应用白皮书”，2024版

天津见合八方光电科技有限公司，是一家专注国产半导体光放大器SOA研发和生产的高科技企业，目前已推出多款半导体光放大器SOA产品(850nm,1060nm,1270nm,1310nm, 1550nm,1625nm)以及增益芯片RSOA产品(850nm,1310nm,1550nm)，公司已建立了万级超净间实验室，拥有较为全面的光芯片的生产加工、测试和封装设备，并具有光芯片的混合集成微封装能力。目前公司正在进行NLL/ECL+SOA的混合集成器件、大功率SOA器件的研发工作，并可对外承接各种光电器件测试、封装和加工服务。