卷积编码是什么 卷积编码原理

本文主要是关于卷积编码的相关介绍，并着重阐述了卷积编码的原理。

卷积编码

在信道编码研究的初期，人们探索、研究出各种各样的编码构造方法，其中包括卷积码。早在1955年，P.Elias首先提出了卷积码。但是它又经历了十几年的研究以后，才开始具备应用价值。在这十几年期间，J.M.Wozencraft提出了适合大编码约束度的卷积码的序列译码，J.L.Massey提出了实现简单的门限译码，A.J.Viterbi提出了适合小编码约束度的卷积码Viterbi算法。20年后，即1974年，L.R.Bahl等人又提出一种支持软输入软输出（SISO，Soft-Input Soft-Output）的最大后验概率（MAP，Maximum A Posteriori）译码——BCJR算法。其中，Viterbi算法有力地推动了卷积码的广泛应用，BCJR算法为后续Turbo码的发现奠定了基础。

编码技术

在卷积码的编码过程中，对输入信息比特进行分组编码，每个码组的编码输出比特不仅与该分组的信息比特有关，还与前面时刻的其他分组的信息比特有关。同样，在卷积码的译码过程中，不仅从当前时刻收到的分组中获取译码信息，还要从前后关联的分组中提取相关信息。正是由于在卷积码的编码过程中充分利用了各组的相关性，使得卷积码具有相当好的性能增益。

1．编码器卷积码编码器实质上是一个有限状态的线性移位寄存器。这个移位寄存器由若干个寄存器单元组成，这些寄存器单元分成组，每组个寄存器单元，相应地可以存储个信息比特。寄存器单元按一定的规则连接到代数运算单元，这样运算单元通过接收这些寄存器单元的输入信息，进行代数运算，将运算结果作为编码比特输出。

编码器的每组输入包含k0个信息比特，第一组寄存器单元存储当前时刻的k0个信息比特，而其他组寄存器单元存储前面时刻的（K−1）k0个信息比特。编码器有n0个编码输出，每个编码输出Yi由当前时刻的输入信息分组以及其他（K−1）个寄存器单元内的信息分组根据相应的连接关系进行模2运算来确定。

因此，一般定义K为编码约束度，说明编码过程中相互关联的分组个数，定义 m=k-1 为编码存储级数，码率 R=k0/n0，这类码通常称为（n0，k0，K）卷积码。在许多实际应用场合，往往采用编码约束度比较小、码率为的卷积码。它们的存储级数都是8，加法器完成二进制加法（模2加）。图中省略了存储当前时刻输入的寄存器单元。

2，1，9）卷积码编码器有一个输入端口、两个输出端口，这两个输出端口分别对应两个生成多项式（使用八进制表示）：561和753。该码率是1/2。在图3-29（b）中，（3，1，9）卷积码编码器有一个输入端口、3个输出端口，这3个输出端口分别对应3个生成多项式（使用八进制表示）：557、663和711。该码率是1/3。TD-LTE系统中采用了（3，1，7）卷积码，存储级数是6，使用了6个寄存器。

这个卷积码的主要优点包括最优距离谱、咬尾编码、译码复杂度小。具体描述见后续章节内容。另外，卷积码也可以按照其他方式进行分类，比如系统码或者非系统码，递归码或者非递归码，最大自由距离码或者最优距离谱码。常用的卷积码一般是非递归的非系统码，而Turbo码常常使用递归的系统卷积码。2．咬尾编码通常卷积码编码器开始工作时都要进行初始化，常常将编码器的所有寄存器单元都进行清零处理。而在编码结束时，还要使用尾比特进行归零的结尾操作（Tailed Termination）。

相对于编码比特而言，尾比特增加了编码开销。TD-LTE系统的卷积码编码器采用了咬尾编码方法，如图3-30所示，编码器开始工作时要进行特殊的初始化，将输入信息比特的最后m个比特依次输入编码器的寄存器中，当编码结束时，编码器的结束状态与初始状态相同。由于这个编码方法没有出现尾比特，因此称为咬尾编码。咬尾编码减少了尾比特的编码开销。对于咬尾编码方法，在译码过程中，由于编码器的初始状态和结尾状态是未知的，因此就需要增加一定的译码复杂度，才能确保好的译码性能。3．性能界卷积码的性能一般使用误比特率（BER，Bit Error Rate）来统计，其理论上界（Upper Bound）一般使用联合界（Union Bound）来确定，即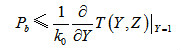（3-13）其中，卷积码的转移函数（Transfer Function），代表非零输入信息比特的转移分支，Y的指数表示输入信息比特的汉明重量，Z代表输出编码比特的转移分支，Z的指数表示输出编码比特的汉明重量。为了进一步分析上述性能界，一般假设最大似然译码（ML，Maximum-Likelihood）、BPSK调制和加性高斯白噪声（AWGN，Additive White Gaussian Noise）信道，则有

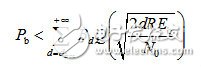
（3-14）其中，Bd是所有重量为d的码字的非零信息比特的重量，为卷积码的自由距离。当信噪比很高时，则式（3-14）近似为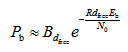（3-15）BPSK调制性能为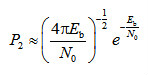（3-16）考虑到误码性能主要是指数项占据主导作用，与未编码系统相比，卷积码的编码增益为（3-17）式（3-17）说明卷积码的渐近性能主要是由自由距离（）决定的。因此，相对而言，卷积码的自由距离越大，其性能越好。以上述二进制卷积码（2，1，9）和（3，1，9）为例，自由距离分别为12和18，编码增益都为7.78dB。实际上，性能最佳的卷积码往往具有最优的距离谱（ODS，Optimum Distance Spectrum）或者重量分布，而且，具有最优距离谱的卷积码也具有最大的自由距离（MFD，Maximum Free Distance）。TD-LTE系统采用了最优距离谱的卷积码。

卷积编码原理

卷积码在一个二进制分组码(n,k)当中，包含k个信息位，码组长度为n，每个码组的(n-k)个校验位仅与本码组的k个信息位有关，而与其它码组无关。为了达到一定的纠错能力和编码效率(=k/n)，分组码的码组长度n通常都比较大。编译码时必须把整个信息码组存储起来，由此产生的延时随着n的增加而线性增加。

为了减少这个延迟，人们提出了各种解决方案，其中卷积码就是一种较好的信道编码方式。这种编码方式同样是把k个信息比特编成n个比特，但k和n通常很小，特别适宜于以串行形式传输信息，减小了编码延时。

与分组码不同，卷积码中编码后的n个码元不仅与当前段的k个信息有关，而且也与前面(N-1)段的信息有关，编码过程中相互关联的码元为nN个。因此，这N时间内的码元数目nN通常被称为这种码的约束长度。卷积码的纠错能力随着N的增加而增大，在编码器复杂程度相同的情况下，卷段积码的性能优于分组码。另一点不同的是：分组码有严格的代数结构，但卷积码至今尚未找到如此严密的数学手段，把纠错性能与码的结构十分有规律地联系起来，目前大都采用计算机来搜索好码。

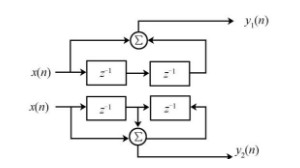
下面通过一个例子来简要说明卷积码的编码工作原理。正如前面已经指出的那样，卷积码编码器在一段时间内输出的n位码，不仅与本段时间内的k位信息位有关，而且还与前面m段规定时间内的信息位有关，这里的m=N-1通常用(n，k，m)表示卷积码(注意：有些文献中也用(n，k，N)来表示卷积码)。图1就是一个卷积码的编码器，该卷积码的n = 2，k = 1，m = 2，因此，它的约束长度nN = n×(m+1) = 2×3 = 6。

图1 (2，1，2)卷集码编码器

在图1中，与 为移位寄存器，它们的起始状态均为零。、与、、之间的关系如下：

(1)

假如输入的信息为D = [11010]，为了使信息D全部通过移位寄存器，还必须在信息位后面加3个零。表1列出了对信息D进行卷积编码时的状态。

表1 信息D进行卷积编码时的状态

输入信息D 1 1 0 1 0 0 0 0

b3b2 00 0 1 1 1 1 0 0 1 1 0 0 0 0 0

输出C1C2 1 1 0 1 0 1 0 0 1 0 1 1 0 0 0 0

描述卷积码的方法有两类，也就是图解表示和解析表示。解析表示较为抽象难懂，而用图解表示法来描述卷积码简单明了。常用的图解描述法包括树状图、网格图和状态图等。基于篇幅原因这里就不详细介绍了。

卷积码的译码方法可分为代数译码和概率译码两大类。代数译码方法完全基于它的代数结构，也就是利用生成矩阵和监督矩阵来译码，在代数译码中最主要的方法就是大数逻辑译码。概率译码比较常用的有两种，一种叫序列译码，另一种叫维特比译码法。虽然代数译码所要求的设备简单，运算量小，但其译码性能(误码)要比概率译码方法差许多。因此，目前在数字通信的前向纠错中广泛使用的是概率译码方法。

维特比译码法简介

viterbi译码算法是一种卷积码的解码算法。缺点是随着约束长度的增加算法的复杂度增加很快。约束长度N为7时要比较的路径就有64条，为8时路径变为128条。 (2<<(N-1))。所以viterbi译码一般应用在约束长度小于10的场合中。

编码(举例约束长度为7)：编码器7个延迟器的状态(0，1)组成了整个编码器的64个状态。每个状态在编码器输入0或1时，会跳转到另一个之中。比如110100输入1时，变成101001(其实就是移位寄存器)。并且输出也是随之而改变的。

解码的过程就是逆过程。算法规定t时刻收到的数据都要进行64次比较，就是64个状态每条路有两条分支(因为输入0或1)，同时，跳传到不同的两个状态中去，将两条相应的输出和实际接收到的输出比较，量度值大的抛弃(也就是比较结果相差大的)，留下来的就叫做幸存路径，将幸存路径加上上一时刻幸存路径的量度然后保存，这样64条幸存路径就增加了一步。在译码结束的时候，从64条幸存路径中选出一条量度最小的，反推出这条幸存路径(叫做回溯)，得出相应的译码输出。

这样的算法在TI的C54x的dsp上使用100M的速率运行，都无法达到数传速度的要求，主要的时间消耗在每条路径的两次比较上，两次比较的时候一共需要从内存中取3个数(上一时刻幸存路径的量度，两个状态跳转相应的输出值)，比较结束以后，还需要对内存写入2个数(幸存路径新的总量度，下一个跳转的状态)，这样，每个时钟节拍需要比较的次数就是64*2次，每次存取数就要5次。一个数据包是256byte，知道解码一包所大概需要的时间。加上其他的开销，最后实验出来的结果是大概0.06m，但是用64k速率传输的时候只要0.03m即可传完。

结语

关于卷积编码的介绍就到这了，希望通过本文能让你对卷积编码有更深的认识。

相关阅读推荐：什么是卷积码

相关阅读推荐：基于VHDL语言并选用FPGA设计了一个卷积码编码器