卷积编码与分组编码的区别及应用案例

　　本文主要是关于卷积编码和分组编码的相关介绍，分别叙述了他俩的不同及其应用案例。

　　一般来说，在编码器复杂性相同的情况下，卷积码的性能优于分组码。

　　卷积码

　　若以（n，k，m）来描述卷积码，其中k为每次输入到卷积编码器的bit数，n为每个k元组码字对应的卷积码输出n元组码字，m为编码存储度，也就是卷积编码器的k元组的级数，称m+1= K为编码约束度m称为约束长度。卷积码将k元组输入码元编成n元组输出码元，但k和n通常很小，特别适合以串行形式进卷积码的编码器行 传输，时延小。与分组码不同，卷积码编码生成的n元组元不仅与当前输入的k元组有关，还与前面m-1个输入的k元组有关，编码过程中互相关联的码元个数为n*m。卷积码的纠错性能随m的增加而增大，而差错率随N的增加而指数下降。

　　线性分组码

　　一个［n，k］线性分组码，是把信息划成k个码元为一段（称为信息组），通过编码器变成长度为n个码元的一组，作为［n，k］线性分组码的一个码字。若每位码元的取值有q种（q为素数幂，q进制），则共有q的k次方个码字。

　　卷积编码的应用

　　卷积码又称连环码，他是非分组（没有固定长度）有记忆编码，但也是一种线性码，码的结构简单，其性能在许多实际情况优于分组码，通常更适用于向前纠错，是一种较为常见的纠错编码。卷积码其编码器在任一规定时间内产生的n个码元，不仅取决于k个信息位，还取决于前N-1段规定时间内的信息位。整个编码过程可以看成是输入信息序列与由移位寄存器和模2加法器的连接方式所决定的另一个序列的卷积，卷积码由此得名。这N段时间内产生的码元数目nN称为卷积码的约束长度。通常将卷积码记作（n，k，N），其中k为一次移入编码器的比特数，n为对应于k比特输入的编码输出。其编码效率为R=k/n。

　　卷积码结构是“信息码、监督位、信息码、监督位…（m1，c1，m2，c2，m3，c3.。.）”。

　　c1=0+m1

　　c2=m1+m2

　　c3=m2+m3

　　

　　（1） 有k个输入信息端，n个输出端（k《n），K-1节移位寄存器（共 需k（K-1）个寄存器单元），称做（n，k，k）卷积码。

　　（2） 通常称K为约束长度（一般来说，约束长度越大，则码字纠错 性能越好）。

　　（3） 码的效率：k/n

　　（4） 编码前，k（K-1）个寄存器单元全部复位清零。

　　（5） 由于一段消息不仅影响当前段的编码输出，还影响其后m段的 编码输出，所以称参量K=m+1为卷积吗的约束比特长度为 K*n·==。

　　（6）注意进入卷积编码器的最后m段消息仍是要编码输出的消息，对这最后m段消息的编码处理，称作卷积编码的结尾处理。一种常见的结尾处理方法是额外输入m段无效的0数据比特，一方面将存储的m段消息编码全部推出，另一方面保证编码器回到全0的初态。

　　function ［out_put，out_G，out_k0］ = convolution（baseband_out）

　　G = ［1，0，1，1;1，1，1，1］; % Generation Matrix G of CC（卷积编码器）

　　k0 = 1; % Number of bits was input into CC

　　input = baseband_out; % input data

　　%查看是否需要补0，输入input必须是k0的整数倍

　　if rem（length（input），k0） 》 0 % whether add 0

　　input=［input，zeros（size（1:k0 - rem（length（input），k0）））］;

　　end

　　n=length（input） / k0; %% 把输入比特按k0分组，n为所得的组数。

　　%检查生成矩阵G的维数是否和k0一致

　　if rem（size（G，1），k0） 》 0 % check the row of G whether identical to k0 %size（A， dim）dim=1表示取矩阵的行数，dim=2表示取矩阵A的列数。

　　error（‘Error，G is not of the right size.’）

　　end

　　%得到约束长度K和输出比特数n0

　　K=size（G，2） / k0; % restrict length

　　n0=size（G，1）; % ouput length

　　%在信息前后加0，使存贮器归0，加0个数为（K-1）*k0个

　　u=［zeros（size（1：（K - 1） * k0）），input，zeros（size（1：（K - 1） * k0））］; % add 0 2（K-1）*k0个以保证编码器是从全0开始，并回到全0状态。

　　u1=u（K * k0：-1:1）; % UU matrix

　　%将加0后的输入序列按每组K*k0个分组，分组是按k0比特增加

　　%从1到K*k0比特为第一组，从1+k0到K*k0+k0为第二组，。。。。，

　　%并将分组按倒序排列。

　　for i=1:n + K - 2 % Grouping 加零以后总共组数

　　u1=［u1，u（（i + K） * k0：-1:i * k0 + 1）］; % Grouping

　　end

　　uu=reshape（u1，K * k0，n + K - 1）; % generate uu， a matrix whose columns are the contents of %生成一列是一组共n+K-1（列）组

　　% conv. encoder at various clock cycles.

　　out_put = reshape（rem（G * uu，2），1，n0 * （K + n - 1））; % % determine the output %rem（G * uu，2）相当与对矩阵的摩尔运算转化成二进制数%

　　out_G = G;

　　out_k0 = k0;

　　% % write the output to the encodetext

　　% result = fopen（encodetext， ‘w’）;

　　% for i = 1:n0*（L+n -1）

　　% fwrite（result， output（i）， ‘bit1’）;

　　% end

　　% fclose（result）

　　分组编码的应用

　　线性分组码（n，k）中许用码字（组）为2k个。定义线性分组码的加法为模2和，乘法为二进制乘法。即1+1=0、1+0=1、0+1=1、0+0=0；1×1=1、1×0=0、0×0=0、0×1=0。且码字与码字的运算在各个相应比特位上符合上述二进制加法运算规则。

　　线性分组码具有如下性质（n，k）的性质：

　　1、封闭性。任意两个码组的和还是许用的码组。

　　2、码的最小距离等于非零码的最小码重。

　　对于码组长度为n、信息码元为k位、监督码元为r＝n－k位的分组码，常记作（n，k）码，如果满足2r－1≥n，则有可能构造出纠正一位或一位以上错误的线性码。

　　下面我们通过（7，4）分组码的例子来说明如何具体构造这种线性码。设分组码（n，k）中，k = 4，为能纠正一位误码，要求r≥3。现取r＝3，则n＝k＋r＝7。我们用a0ala2a3a4a5a6表示这7个码元，用S1、S2、S3表示由三个监督方程式计算得到的校正子，并假设三位S1、S2、S3校正子码组与误码位置的对应关系如表12.2所示。

　　

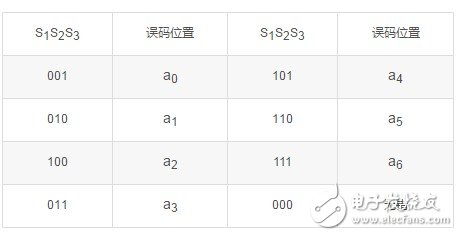
　　在接收端收到每个码组后，计算出S1、S2、S3，如果不全为0，则表示存在错误，可以由表12.2确定错误位置并予以纠正。例如收到码组为0000011，可算出S1S2S3=011，由表12.2可知在a3上有一误码。通过观察可以看出，上述（7，4）码的最小码距为dmin＝3，它能纠正一个误码或检测两个误码。如果超出纠错能力则反而会因“乱纠”出现新的误码。

　　

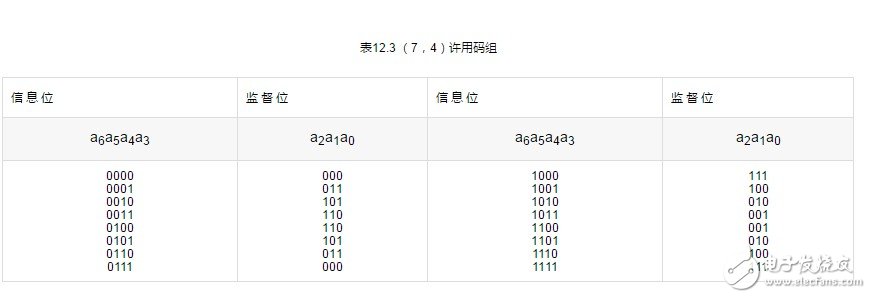
　　上述方法构造的能纠正单个误码的线性分组码又称为汉明码。它具有以下一些特点：码长n＝2m－1，最小码距为d＝3，信息码长k＝2n－m－1，纠错能力t＝1，监督码长r＝n－k＝m。这里m为≥2的正整数。给定m后，就可构造出汉明码（n，k）。

　　（7，4）汉明码的编译码仿真：

　　

　　

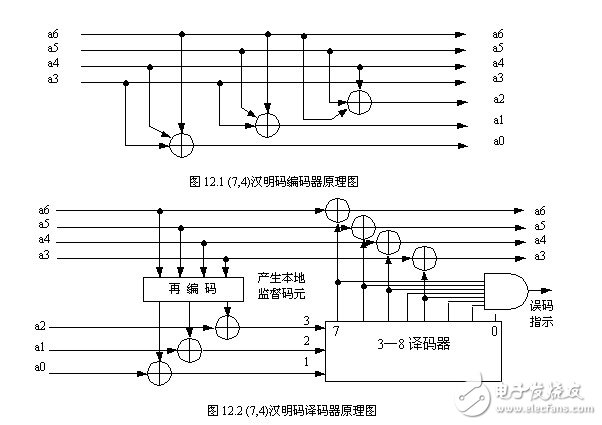
　　图12.1所示为（7，4）汉明码的编码器电路原理图，图12.2为对应的译码器电路原理图。根据上述两图可构建如图12.3所示的仿真原理图。该仿真原理图包含两个子系统，分别是（7，4）汉明码的编码器和译码器。仿真时的信号源采用了一个PROM，并由用户自定义数据内容，数据的输出由一个计数器来定时驱动，每隔一秒输出一个4位数据（PROM的8位仅用了其中4位），由编码器子系统编码转换后成为7位汉明码，经过并串转换后传输，其中的并串、串并转换电路使用了扩展通信库2中的时分复用合路器和分路器图符，该合路器和分路器最大为16位长度的时隙转换，这里定义为7位时隙。此时由于输入输出数据的系统数据率不同，因此必须在子系统的输入端重新设置系统采样率，将系统设置为多速率系统。因为原始4位数据的刷新率为1Hz，因此编码器的输入端可设置重采样率位10Hz，时分复用合路器和分路器的数据帧周期设为1秒，时隙数位7，则输出采样率为输入采样率的7倍，即70Hz。如果要加入噪声，则噪声信号源的采样率也应设为70Hz。图12.3是（7，4）汉明码编码器的仿真子系统原理图，图12.4是其对应的译码器的仿真子系统原理图。图12.5为经过并串转换后的（7，4）汉明码输出波形图，这里仅设置了4秒时间长度的仿真，输出的4个数据为0、1、3、4，对应的（7，4）汉明码码字为（0000000）、（0001011）、（0011110）、（0100110），注意串行传输的次序是先低后高的次序（LSB）。

　　当然，我们也可以不通过并串转换，直接并行传输、译码。这样可以在7位汉明码并行传输时人为对其中的一位进行干扰，并观察其纠错的情况。通过仿真实验可以发现，出现两位以上错误时汉明码就不能正确纠错了。因此，在要求对多位错误进行纠正的应用场合，就要使用别的编码方式了，如BCH码、RS码、卷积码等。

　　结语

　　关于卷积编码与分组编码的不同就介绍到这了，希望本文能让你对卷积编码与分组编码区别有更深的认识。

           相关阅读推荐：分组码 是什么意思

           相关阅读推荐：卷积编码是什么