卷积码编码器怎么画 浅谈卷积码编码器设计

本文主要是关于卷积码编码器的相关介绍，并对卷积码编码器的设计进行了详尽的阐述。

卷积码编码器

卷积码是通信编码中纠错编码的一种，它可以将原来的信息码打乱，这时尽管出现大面积突发性错误，这些可以通过解交织器来进行分散，从而将大面积的错误较为平均地分散到不同的码段，利于信道纠错的实现。卷积编码器即为实现卷积码编码的电路。

卷积码拥有良好的纠错性能，是一种被广泛应用于移动通信的信道编码系统。一个（n，k，m）卷积码编码器由k个输入，具有m阶存储的n个输出的线形时序电路实现。通常， n和k是较小的整数，且

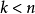
，但m比较大。当

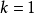
时，信息序列不再分成小块，以便可以连续处理。卷积码（n，k，m）表示码率

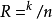
，编码器级数

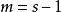
，其中s是码约束长度。 [1] 

反向CDMA信道使用（3，1，8）卷积码，码率

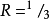
，约束长度为9，由于

，

，

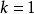
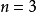
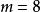
，则该卷积编码器包含单个输入端，一个8级移位寄存器，三个模2加法器和一个3向编码器输出的连续转向器。编码器每输入一位信息比特将产生三位编码输出。这些编码符号中，第一个输出符号

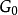
是生成序列

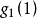
编码产生的符号，第二个输出符号

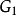
是由生成序列

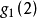
编码产生的符号，最后一个输出符号

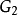
是由生成序列

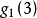
编码产生的符号，如下图所示。

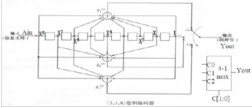
该电路由一个八位寄存器、三个码生成逻辑、一个时隙发生器和一个四选一复用器构成。mux的输入为

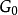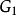和和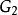，码选择信号C[1:0]和clk1由时隙发生器产生，输出信号即为整个电路的输出。

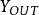卷积编码器的初始状态用rst异步清零信号置为0，

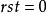
时，电路清零。 卷积编码器的初始状态全为0，初始状态之后输出的第一个编码符号由生成序列

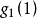
编码产生。这里，三个生成序列分别为

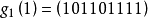
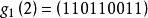
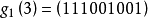
即三个生成多项式分别为：

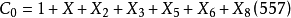
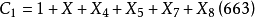
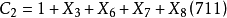
卷积码编码器设计

卷积码的编码器一般都比较简单。

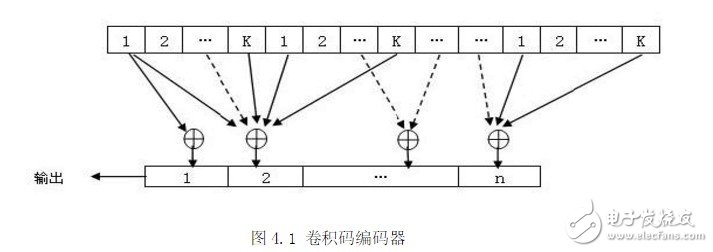
图4.1是一般情况下的卷积码编码器框图。它包括NK级的输入移位器，一组n个模2和加法器和n级的输出移位寄存器。对应于每段k比特的输入序列，输出n个比特。由图可知，n个输出比特不但与当前的k个输入比特有关，而且与以前的（N-1）k个输入信息比特有关。整个编码过程可以看成是输入信息序列与由移位寄存器和模2加法器的连接方式所决定的另一个序列的卷积，卷积码由此得名。本文采用的是冲击响应描述法编码思想。

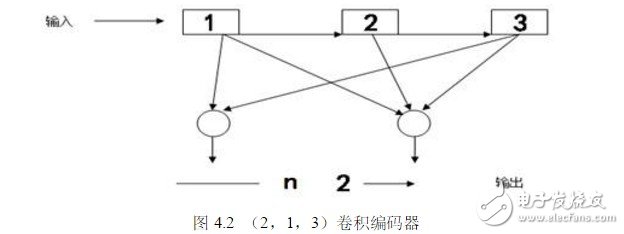
图4.2是卷积编码器（2，1，3）卷积编码器的方框图。左边是信息的输入。下面是系统位输出和奇偶校验位输出。其中有3个移位寄存器和一个模块化2加法器。简单地说，信息位由移位寄存器和模2加法器一起输出，产生一个系统位和一个校验位。可以看出，当每个比特被输入时，移位在移位寄存器中被移动到右边。原来的第三个寄存器被删除。可见卷积编码不仅与输入比特有关，而且与前面的3-1比特相关。约束长度为3。这里，k＝1和n＝2是r＝k/n＝1/2〔3〕。

卷积码的树状图 

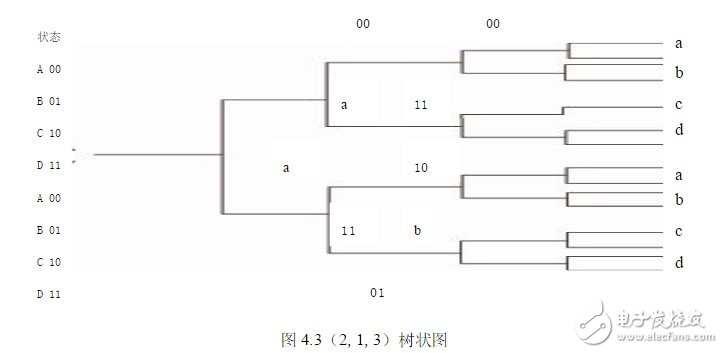
对于图4.2所示的（2,1,3）卷积码编码电路，其树状图如下图4.3所示，这里，分别用a，b，c和d表示寄存器的4种状态：00,01,10和11，作为树状图中每条支路的节点。以全零状态a为起点，当输入位信息位为0时，输出码元c1c2=00，寄存器保持状态a不变，对应图中从起点出发的上支路；当输入位为1时，输出码元c1c2=11，寄存器则转移到状态b，对应图中的下支路；然后再分别以这两条支路的终结点a和b作为处理下一位输入信息的起点，从而得到4条支路，以此类推，可以得到整个树状图。如下图4.3

 卷积码的网格图 

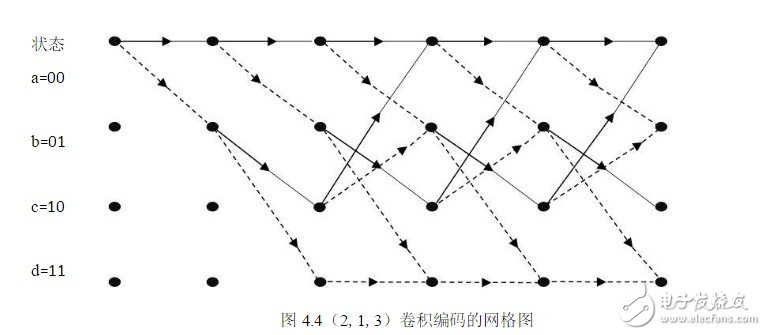
状态图可以完整的描述编码器的工作过程，但是其只能显示状态转移的过程而不能显示状态转移发生的时刻，由此引出用来表示卷积码的另一种常用方法——网格图。网格图就是时 间与对应状态的转移图，在网格图中每一个点表示该时刻的状态，状态之间的连线表示状态转移。通过观察网格图可以发现在网格图中输入信息x（n）并没有标出，但如观察到转移后的状态表示（x（n），x（n-1））就可以发现输入信息已经隐含在转移后的状态中[4]。 

如下图4.4是（2,1,3）卷积编码的网格图。

卷积编码器VHDL仿真波形

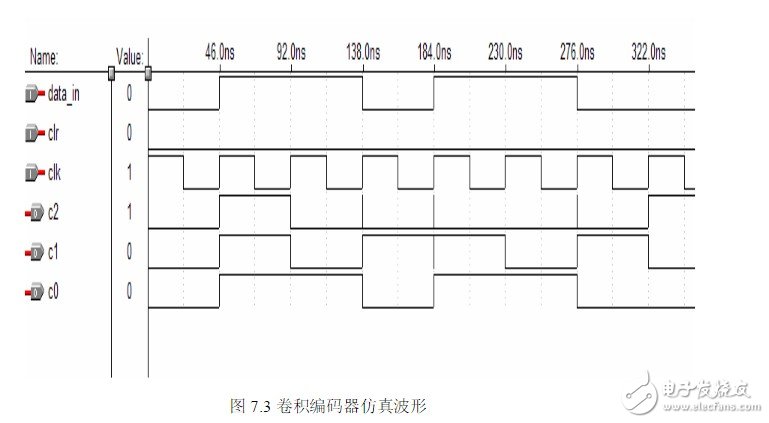
卷积编码器VHDL仿真波形如图7.3所示。输入信息序列DATAIN＝“11011”在仿真前设置，速率为32 kb/s。仿真结果表明，卷积编码的输出为“111100100010110100100”，速率为96 kb/s，与理论分析相一致。

结语

关于卷积码编码器设计的相关介绍就到这了，希望通过本文能让你对卷积码编码器有更深的认识，如有不足之处欢迎指正。

相关阅读推荐：什么是卷积码

相关阅读推荐：什么是卷积