卷积码状态图怎么画 卷积编码器状态图画法

本文主要是关于卷积码的相关介绍，依据卷积码就它的状态图的画法展开了介绍，并着重阐述了卷积编码器状态图画法。

卷积码

卷积码，将k个信息比特编成n个比特，但k和n通常很小，特别适合以串行形式进行传输，时延小。与分组码不同，卷积码编码后的n个码元不仅与当前段的k个信息有关，还与前面的N-1段信息有关，编码过程中互相关联的码元个数为nN。卷积码的纠错性能随N的增加而增大，而差错率随N的增加而指数下降。在编码器复杂性相同的情况下，卷积码的性能优于分组码。

卷积码是1955年由Elias等人提出的，是一种非常有前途的编码方法。我们在一些资料上可以找到关于分组码的一些介绍，分组码的实现是将编码信息分组单独进行编码，因此无论是在编码还是译码的过程中不同码组之间的码元无关。卷积码和分组码的根本区别在于，它不是把信息序列分组后再进行单独编码，而是由连续输入的信息序列得到连续输出的已编码序列。即进行分组编码时，其本组中的n-k个校验元仅与本组的k个信息元有关，而与其它各组信息无关；但在卷积码中，其编码器将k个信息码元编为n个码元时，这n个码元不仅与当前段的k个信息有关，而且与前面的（m－1）段信息有关（m为编码的约束长度）。

同样，在卷积码译码过程中，不仅从此时刻收到的码组中提取译码信息，而且还要利用以前或以后各时刻收到的码组中提取有关信息。而且卷积码的纠错能力随约束长度的增加而增强，差错率则随着约束长度增加而呈指数下降 。卷积码（n，k，m） 主要用来纠随机错误，它的码元与前后码元有一定的约束关系，编码复杂度可用编码约束长度m*n来表示。

一般地，最小距离d表明了卷积码在连续m段以内的距离特性，该码可以在m个连续码流内纠正（d-1）/2个错误。卷积码的纠错能力不仅与约束长度有关，还与采用的译码方式有关。总之，由于n，k较小，且利用了各组之间的相关性，在同样的码率和设备的复杂性条件下，无论理论上还是实践上都证明：卷积码的性能至少不比分组码差。

编码原理

以二元码为例，编码器如图。输入信息序列为u＝(u0，u1，…)，其多项式表示为u(x)＝u0+u1x＋…＋ulxl＋…。编码器的连接可用多项式表示为g(1,1)(x)＝1+x+x2和g(1,2)(x)＝1+x2，称为码的子生成多项式。它们的系数矢量g(1,1)=(111)和g(1,2)=(101)称作码的子生成元。以子生成多项式为阵元构成的多项式矩阵G(x)＝[g(1,1)(x),g(1,2)(x)]，称为码的生成多项式矩阵。由生成元构成的半无限矩阵

称为码的生成矩阵。其中(11,10,11)是由g(1,1)和g(1,2)交叉连接构成。编码器输出序列为c＝u·G，称为码序列，其多项式表示为c(x)，它可看作是两个子码序列c(1)(x)和c(2)(x)经过合路开关S合成的，其中c(1)(x)＝u(x)g(1,1)(x)和c(2)(x)＝u(x)g(1,2)(x),它们分别是信息序列和相应子生成元的卷积，卷积码由此得名。

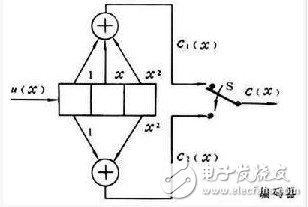
在一般情况下，输入信息序列经过一个时分开关被分成k0个子序列,分别以u(x)表示,其中i=1，2,…k0，即u(x)＝[u(x),…,u(x)]。编码器的结构由k0×n0阶生成多项式矩阵给定。输出码序列由n0个子序列组成，即c(x)＝[c(x),c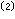(x)，…，c(x)]，且c(x)=u(x)·G(x)。若m是所有子生成多项式g(x)中最高次式的次数，称这种码为(n0，k0，m)卷积码。

卷积码状态图怎么画

将编码器寄存器中的内容组合（x（n-1）、x（n-2））定义为编码器状态。如仍以前面所举的例子(2，1，2)为例，则该编码器的状态有四种：00，10，01和11，下面分别用a，b，c，d来代替。编码器在每一个时钟沿打入一个输入信息x（n），因此图示寄存器组合内容就变为（x（n），x（n-1））即状态发生了转移，并同时输出G0（n）、G1（n）。由此我们可以将图所示编码过程用右图所示的状态图表示。

由图所示，随着信息序列不断输入，编码器就不断从一个状态转移到另一个状态并同时输出相应的码序列，所以图3所示状态图可以简单直观的描述编码器的编码过程。因此通过状态图很容易给出输入信息序列的编码结果，假定输入序列为110100，首先从零状态开始即图示a状态，由于输入信息为“1”，所以下一状态为b并输出“11”，继续输入信息“1”，由图知下一状态为d、输出“01”……其它输入信息依次类推，按照状态转移路径a->b->d->c->b->c->a输出其对应的编码结果“110101001011”。

卷积码的其它表示方法

1. 多项式法

多项式法就是由卷积码的生成多项式直接得出其编码器的结构图。如前面例子中的(2，1，2)卷积码的生成多项式矩阵为：G(D)=[1 D D2,1 D2]

其中，D是延迟算子，生成多项式的第一项为1 D D2，表示输出编码的第一个码元等于输入码元x（n）与前两个时刻输入的码元x（n-1）、x（n-2）的模2和，同理第二项类似。

2. 网格图

状态图可以完整的描述编码器的工作过程，但是其只能显示状态转移的过程而不能显示状态转移发生的时刻，由此引出用来表示卷积码的另一种常用方法——网格图。网格图就是时间与对应状态的转移图（如图），在网格图中每一个点表示该时刻的状态，状态之间的连线表示状态转移。通过观察网格图可以发现在网格图中输入信息x（n）并没有标出，但如观察到转移后的状态表示（x（n），x（n-1））就可以发现输入信息已经隐含在转移后的状态中。在图中还可以发现两个网格图不同主要集中在转移后状态位置不同。重新排序结构（即所谓蝶型结构）是为了优化运算而设计的，因为其中蝶型与蝶型之间是相互独立的。

下面就让我们来看看网格图是如何描述卷积编码过程的：仍以（2，1，2）为例，假定输入序列为1011010100，起始状态（零时刻）为状态a（零状态）。第一个有效时钟沿来临后，编码器接收到输入信息“1”，根据图所示网格图知该时刻（即时刻1）状态为b，并输出其对应的编码结果“11”，同样在下一个时刻（时刻2）接收到输入信息“0”，状态变为c并输出“10”，接下来的输入数据依次类推……，由此我们可以用网格图作出该例子的卷积编码过程，如图5所示，其中两个状态连线之间的信息为输出结果。

卷积编码器状态图画法

状态图是关于系统状态变化的描述，它将由系统的输入，根据当前的系统状态，影响系统的输出。卷积码编码器存储的L-1段消息，既要因新的消息输入而改变，又要影响当前的编码输出，把卷积码编码器的移位寄存器中任一时刻所存储的信息称为卷积码编码器的一个状态。

（n,k,L）卷积码共有2^(k*(L-1))个状态，每次输入k比特只有2^k种状态变化，所以，每个状态只能转移到全部状态的某个子集(2^k个状态)中去，每个状态也只能由全部状态的某个子集（2^k个状态）转移而来。

（2,1,2）卷积码编码器包含2级移位寄存器和2个模2加法器。2级移位寄存器共有2^2=4种不同状态，定义为S0(00)、S1(01)、S2(10)和S3(11)四种状态。在每个时刻，输入的1个比特信息，当前状态将转为4种状态中的任何一种。

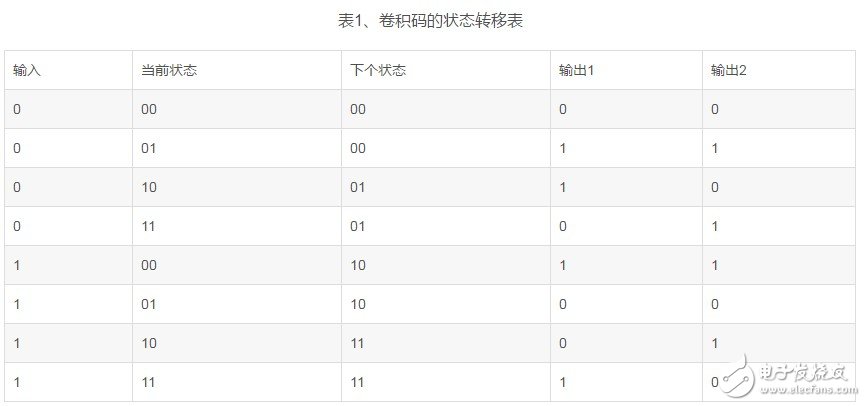
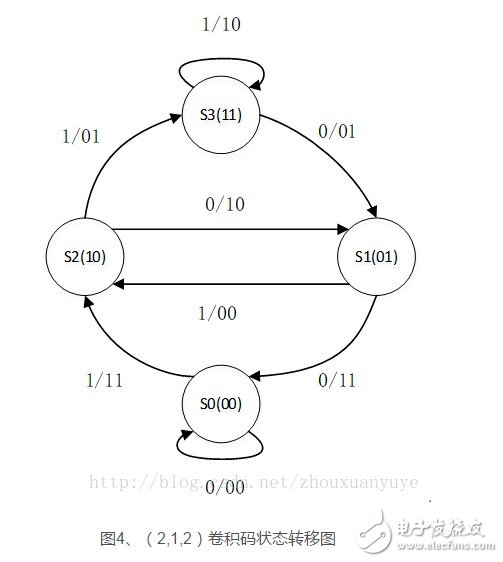
状态表类似查找表，原理即根据当前的输入和当前的状态，可以从表中查得输出信息。图4为卷积码的状态转移图，图中的状态转移表示“输入/输出1输出2”。

结语

关于卷积编码器状态图画法的介绍就到这了，希望通过本文能让你对卷积编码器状态图画法有更深的认识，如有不足之处欢迎指正。

相关阅读推荐：什么是卷积码

相关阅读推荐：卷积码编码器怎么画