基于VHDL的卷积编码实现 详解卷积编码的应用

在现代数字通信中，为降低数据传输的误码率，提高通信质量及其可靠性，常在通信中采用纠错编码技术。

本文主要介绍的就是关于卷积编码的相关介绍，希望通过本文能让你对卷积编码有更深的认识。

卷积编码

在信道编码研究的初期，人们探索、研究出各种各样的编码构造方法，其中包括卷积码。早在1955年，P.Elias首先提出了卷积码。但是它又经历了十几年的研究以后，才开始具备应用价值。在这十几年期间，J.M.Wozencraft提出了适合大编码约束度的卷积码的序列译码，J.L.Massey提出了实现简单的门限译码，A.J.Viterbi提出了适合小编码约束度的卷积码Viterbi算法。20年后，即1974年，L.R.Bahl等人又提出一种支持软输入软输出（SISO，Soft-Input Soft-Output）的最大后验概率（MAP，Maximum A Posteriori）译码——BCJR算法。其中，Viterbi算法有力地推动了卷积码的广泛应用，BCJR算法为后续Turbo码的发现奠定了基础。

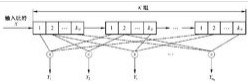
编码技术

在卷积码的编码过程中，对输入信息比特进行分组编码，每个码组的编码输出比特不仅与该分组的信息比特有关，还与前面时刻的其他分组的信息比特有关。同样，在卷积码的译码过程中，不仅从当前时刻收到的分组中获取译码信息，还要从前后关联的分组中提取相关信息。正是由于在卷积码的编码过程中充分利用了各组的相关性，使得卷积码具有相当好的性能增益。

编码器图中，编码器的每组输入包含k0个信息比特，第一组寄存器单元存储当前时刻的k0个信息比特，而其他组寄存器单元存储前面时刻的（K−1）k0个信息比特。编码器有n0个编码输出，每个编码输出Yi由当前时刻的输入信息分组以及其他（K−1）个寄存器单元内的信息分组根据相应的连接关系进行模2运算来确定。

因此，一般定义K为编码约束度，说明编码过程中相互关联的分组个数，定义 m=k-1 为编码存储级数，码率 R=k0/n0，这类码通常称为（n0，k0，K）卷积码。在许多实际应用场合，往往采用编码约束度比较小、码率为的卷积码。如图3-29所示的两种卷积码（2，1，9）和（3，1，9），它们的存储级数都是8，加法器完成二进制加法（模2加）。图中省略了存储当前时刻输入的寄存器单元。在图3-29（a）中，（2，1，9）卷积码编码器有一个输入端口、两个输出端口，这两个输出端口分别对应两个生成多项式（使用八进制表示）：561和753。该码率是1/2。在图3-29（b）中，（3，1，9）卷积码编码器有一个输入端口、3个输出端口，这3个输出端口分别对应3个生成多项式（使用八进制表示）：557、663和711。该码率是1/3。

TD-LTE系统中采用了（3，1，7）卷积码，存储级数是6，使用了6个寄存器。这个卷积码的主要优点包括最优距离谱、咬尾编码、译码复杂度小。具体描述见后续章节内容。另外，卷积码也可以按照其他方式进行分类，比如系统码或者非系统码，递归码或者非递归码，最大自由距离码或者最优距离谱码。常用的卷积码一般是非递归的非系统码，而Turbo码常常使用递归的系统卷积码。

咬尾编码通常卷积码编码器开始工作时都要进行初始化，常常将编码器的所有寄存器单元都进行清零处理。而在编码结束时，还要使用尾比特进行归零的结尾操作（Tailed Termination）。相对于编码比特而言，尾比特增加了编码开销。TD-LTE系统的卷积码编码器采用了咬尾编码方法。

编码器开始工作时要进行特殊的初始化，将输入信息比特的最后m个比特依次输入编码器的寄存器中，当编码结束时，编码器的结束状态与初始状态相同。由于这个编码方法没有出现尾比特，因此称为咬尾编码。咬尾编码减少了尾比特的编码开销。对于咬尾编码方法，在译码过程中，由于编码器的初始状态和结尾状态是未知的，因此就需要增加一定的译码复杂度，才能确保好的译码性能。3．性能界卷积码的性能一般使用误比特率（BER，Bit Error Rate）来统计，其理论上界（Upper Bound）一般使用联合界（Union Bound）来确定，即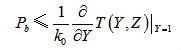（3-13）其中，卷积码的转移函数（Transfer Function），代表非零输入信息比特的转移分支，Y的指数表示输入信息比特的汉明重量，Z代表输出编码比特的转移分支，Z的指数表示输出编码比特的汉明重量。为了进一步分析上述性能界，一般假设最大似然译码（ML，Maximum-Likelihood）、BPSK调制和加性高斯白噪声（AWGN，Additive White Gaussian Noise）信道，则有

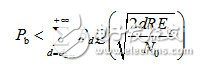
（3-14）其中，Bd是所有重量为d的码字的非零信息比特的重量，为卷积码的自由距离。当信噪比很高时，则式（3-14）近似为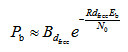（3-15）BPSK调制性能为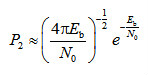（3-16）考虑到误码性能主要是指数项占据主导作用，与未编码系统相比，卷积码的编码增益为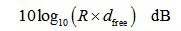（3-17）式（3-17）说明卷积码的渐近性能主要是由自由距离（）决定的。因此，相对而言，卷积码的自由距离越大，其性能越好。以上述二进制卷积码（2，1，9）和（3，1，9）为例，自由距离分别为12和18，编码增益都为7.78dB。实际上，性能最佳的卷积码往往具有最优的距离谱（ODS，Optimum Distance Spectrum）或者重量分布，而且，具有最优距离谱的卷积码也具有最大的自由距离（MFD，Maximum Free Distance）。TD-LTE系统采用了最优距离谱的卷积码。

基于VHDL的卷积编码实现

在现代数字通信中，为降低数据传输的误码率，提高通信质量及其可靠性，常在通信中采用纠错编码技术。其中卷积码就是一种具有较强纠错能力的纠错码。由于 Vitebrbi 译码算法比较容易实现，卷积码得到了广泛应用。本课题简明地介绍了用 EDA 技术实现卷积码编码器的实现。 卷积码纠错性能常常优于分组码，是一种性能优越的信道编码。由于码字之间的相关性，其编码器要利用移位寄存器来存储状态。

随着纠错编码理论研究的不断深入，卷积码的实际应用越来越广泛。卷积码作为通信系统中重要的编码方式，以其良好的编码性能，合理的译码方式，被广泛应用。本文在阐述卷积码编码器基本工作原理的基础上，给出了（2，1，2）卷积编码器的 VHDL 设计，在QuartusⅡ环境下进行了波形功能仿真，并下载到 EP1C6T144C8N 芯片上进行验证，最终实现输入四位序列，编码输出八位通过指示灯显示。
 

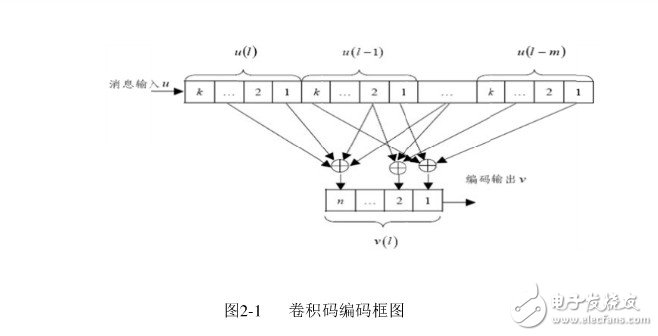
卷积编码的编码约束长度定义为：串行输入比特通过编码其所需的移位次数，它表示编码过程中相互约束的分支码数，所以具有m级移位寄存器的编码器得约束长度为m十1，有时也说（m十1）n为卷积编码的编码约束长与分组编码一样。

卷积编码的编码效率也定义为R=k/η，与分组码具有固定码长η不同，卷积码没有，我们可通过周期性地截断来获得分组长度为了达到清空编码移位寄存器数据bit的目的，需要在输入数据序列末尾附加若于0bit。由于附加的0不包含任何信息，因而，有效编码效率降至kn以如果截断周期取值较大，则有效编码效率会逼近kn。

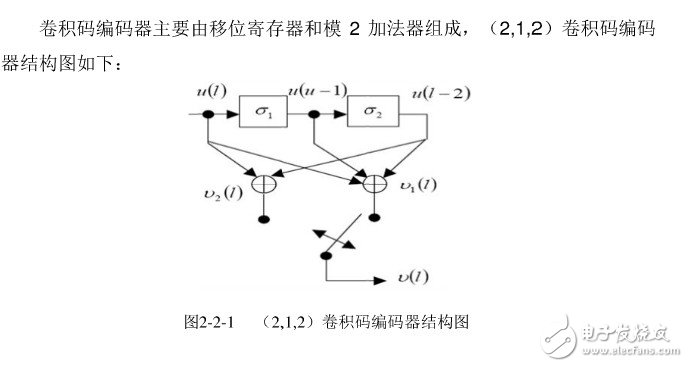
图中的小框表示寄存器的状态，连接小框的箭头表示状态转移的方向，两线旁的数字表示：输出分支码字/输入信息比特。状态图简明的表示了在某一时刻编码器的输入比特和输出分支码字的关系。

结语

关于卷积编码的相关介绍就到这了，如有不足之处欢迎指正。

相关阅读推荐：什么是卷积码

相关阅读推荐：什么是卷积