基于 Vertibi算法的卷积码解码设计实现

本文主要是基于 Vertibi算法的卷积码解码设计实现的相关介绍，并就卷积编码展开了详尽的阐述。

卷积编码

在信道编码研究的初期，人们探索、研究出各种各样的编码构造方法，其中包括卷积码。早在1955年，P.Elias首先提出了卷积码。但是它又经历了十几年的研究以后，才开始具备应用价值。在这十几年期间，J.M.Wozencraft提出了适合大编码约束度的卷积码的序列译码，J.L.Massey提出了实现简单的门限译码，A.J.Viterbi提出了适合小编码约束度的卷积码Viterbi算法。20年后，即1974年，L.R.Bahl等人又提出一种支持软输入软输出（SISO，Soft-Input Soft-Output）的最大后验概率（MAP，Maximum A Posteriori）译码——BCJR算法。其中，Viterbi算法有力地推动了卷积码的广泛应用，BCJR算法为后续Turbo码的发现奠定了基础。

浅谈卷积编码

实际上编码过程就可以应用一个经典的“状态机模型”，而状态机模型的不同表达方式也使得整个编码过程在时间和空间两个维度展现出来。例如，状态图，即是一个很好的表示状态变化的图形。但是由于循环反复的利用状态信息，但在时间上，并未很好的体现卷积码的编码过程。相比，树形图，在时间上进行延展，很直观的表现出状态变化的过程，但是状态信息未重复利用，使得存储空间大小得到限制（指数增加）。最后，网格图很好的展现了时间和空间两个维度信息，很适合分析卷积码的编码过程。而用Matlab实现卷积码编码的时候，我按照传统卷积码编码方法（只考虑实现，未考虑算法的优化），中规中矩的编码思路，但在速度上，并未得到很好的保证。而老师给的编程思想则是：给出每个以为寄存器中随时间变化存储的二进制信息。例如，4个移位寄存器，则每个移位寄存器存储的信息分别为：[abcdefg000；0abcdefg00；00abcdefg0；000abcdefg]，所以矩阵的纵列信息即为所有寄存器中瞬时状态信息，而生成多项式中数值为‘1’的移位寄存器存储比特信息将参与mod2运算。这样利用矩阵的乘法直接完成查找移位寄存器中对应生成多项式数值为‘1’位置的信息。相比我的编码思路（循环查找寄存器里对应生成多项式数值为‘1’的信息），运算速度大大提升。同时，在对状态机模型的认识也进一步深入，即，编码过程为移位寄存器中状态不断变化的过程。（编码用‘状态’描述，并且将‘状态’融入到算法实现中）

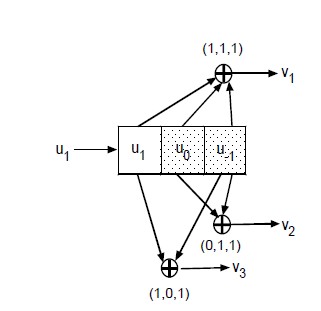
在完成解码的过程中，找了许多关于Viterbi算法的papers，但在编码过程对状态机模型的认识过程中，意识到，解码过程对状态机模型的依赖。实际上，Viterbi算法就是一个在状态机模型基础上不断减少可能路径的一个过程。因为解码是编码的一个逆序过程，接受比特和初始状态是我们已知的信息，我们无法找到一个逆序的算法来计算输入比特信息。

所以Viterbi算法利用的就是‘重新编码’的思想，计算每条路径可能的概率值大小，用概率最大的路径来模拟编码过程。从而得到输入比特信息。而状态机模型的应用大大提升了解码过程寻找正确路径的速度。而在用matlab算法实现的过程中，老师用initial state和next state作为矩阵的行列号，查找输入比特的速度比我实现时不断循环查找状态表提升很多，也使最后所画的误码率对比图达到理想的接受比特个数（提高了系统的运算能力）。

还记得答辩时候老师问我的那个问题：如果接受比特中错误比特的数量一定（假设都是10个），那么错误比特均匀分布和集中分布两种方式哪个误码率性能比较好？听到问题的时候，脑袋想过的编码过程，错误比特的分布情况，所以回答的一塌糊涂。后来才在老师的解释下，明白了题目的意思。老师想问的是，错误比特（信道噪声影响）的排列分布对解码时误码率性能的影响。卷积码编码的时候就假设，每个block是相对独立的，而瞬时编码的时候，输出比特不仅仅与当前的输入比特信息有关，还与之前的若干blocks里的信息有关（联合概率）。所以在解码的时候，每组接收比特的信息也与之前的若干比特信息是相关联的。

所以，如果误码比较集中，在Viterbi时，权值的计算时就会相对增加权值的比重（大的越大，小的越小），容易将该条路径淘汰。而误码分散排列时，一些权值有可能比较接近，无法淘汰。因此误码集中分布的情况，系统的误码率性能较好。老师的问题，一定程度上又深化了我对整个系统认识的深度。不仅仅在编码上，而且在解码端理解卷积码的意义：用相邻信息编码、解码，使得信息能在信道中准确传输。

而抛开状态机模型的应用，Viterbi算法的关键在于路径选择的权值（metric）问题。权值的计算的优化能大大提升系统误码率的大小。这样，就到了最后一个问题，硬判决和软判决对系统误码率的提升能力分析。从星座图的角度看，误码率性能体现在是否能够找到正确的接收比特组合信息，即纠正错码的距离（纠正错码的能力）。

硬判决在解调时直接将接受比特映射到‘0’，‘1’的星座图空间上，那么使用汉明距离（100%的概率决定接收比特信息）就可以将接收比特投射到相应的星座图位置，这样，如果产生错码，硬判决解码的纠正错码的距离将很大（正方形的边长或对角线）。

而软判决解调时则在‘0’和‘1’直接设置多个门限，使得接收比特可以投射到范围内的某个区域里，而通过区域比特的组合信息，使用欧几何距离（用一定概率值分析接收比特信息）计算最准确的接收比特，这样，如果产生错码，软判决纠正错码的距离将变小（图b中实点位置，纠正错码距离提升），从而得到相对准确的接收比特。因此，软判决的解码过程误码率性能将优于硬判决。

基于 Vertibi算法的卷积码解码设计实现

关于Vertibi算法的原理，网上相关的资料很多，况且来看这篇文章的同学对原理应该不陌生，在这里只是简单提提。我们以（2,1）卷积编码器为例，其核心可用下面几幅图表示 

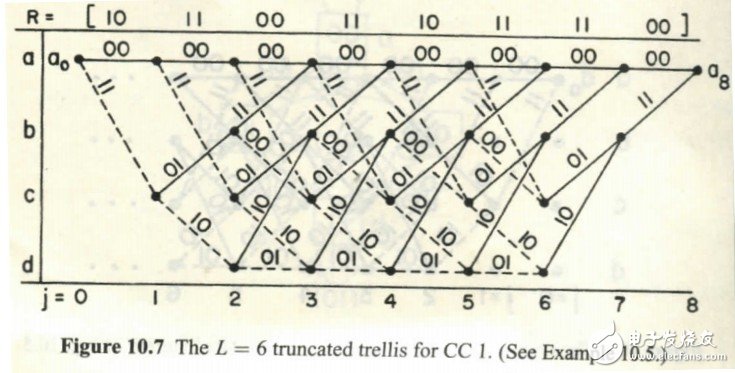
每个卷积编码器可用状态转移来表示，因此图中a,b,c,d代表编码器所处的4个状态，而j表示时刻，实线表示输入为1，虚线表示输入为0，而线上的数字表示输入对应的输入；打个比方，图中(a,0)点到(c,1)点的连接表示：当输入为0时，寄存器的状态从0时刻的a（我们设为两个寄存器的状态全为0，记为00）到1时刻的c（记为10），且伴随着输出为11

而Vertibi译码则是从上图中找出一条路，使这条路径对应的输出序列与输入序列的汉明距离最小（既“最像”）

面对这种问题，我们首先想到的便是树的深度遍历，既找出所有路径然后看看谁“最像”。然而。Vertibi就是靠这个成为南加州大学知名校友，创立高通公司，并且成功让系主任花半节课将他的生平，自然有其妙♂处。

请看下图 

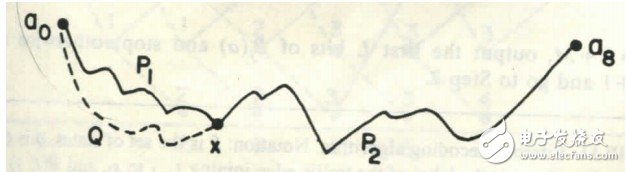
它阐述了一个定理：如果P是最短路径，对于P上任意一点x，P1一定是最短路径。 
这个定理可以很轻松的用反证法证明

之后的东西好难用语言描述所以我们直接看伪代码吧 

在这里做些解释 

首先定义路径长度为两个状态转移时的输出序列与相应的输入序列的汉明距离

u[j][s]代表J时刻到达s状态的累计路径长度

l[t][s]代表从t状态转到l状态的的路径长度

B[s]代表s状态的对应解码序列

由于最后路径会回到a状态（既寄存器为00状态），因此按照以上方法执行后，B(a)即为结果

int vertibi（int *seq， int seqLen， int outnum，int innum，int stat［］［MAXSTAT］， int statRow， int out［］［MAXSTAT］［MAXBLOCK］，int *res ， int *fixed） {

/*seq为输入序列，seqLen为输入序列长度，outnum为输出数（对于（2，1）卷积码而言为2），innum位输入数（对于（2，1）卷积码而言为1），stat为二维的状态转移表（比如说，若状态a转到状态c需要输入1，则stat［1］［3］=1，无法转移的值设为-1），statRow为状态转移表的列数（既状态数量），out［］［］［］为三维的数组，存储两个状态间转换时的输出序列，res为解码结果序列，fixed为纠正后的输入序列*/

int u［MAXJ］［MAXSTAT］;

int B［MAXSTAT］［MAXLEN/2］;

int BB［MAXSTAT］［MAXLEN］; /*BB［s］表示s状态对应的纠正后序列*/

memset（u， 0， sizeof（u））;

memset（B， 0， sizeof（B））;

memset（BB， 0， sizeof（BB））; /*置零*/

for （int j = 0; j 《 statRow; j++） {

if （！j） u［0］［j］ = 0;

else u［0］［j］ = 100;

}

/*因为状态的起点为状态a，所以在0时刻除了状态a（即u［0］［0］）外其它值都设为无穷大（此处定义为100）*/

int curSeq［MAXBLOCK］; //当前用于计算路径距离的输入序列段

for （int J = 1; J 《 seqLen/（outnum*innum）; J++） {//此处的J代表时刻

for （int ii = 0; ii 《 outnum*innum; ii++） {

curSeq［ii］ = seq［（J-1）*outnum*innum+ii］;

} //从输入中取出当前段

for （int i = 0; i 《 statRow; i++） { //遍历J时刻的状态

int min = 100;

int minj = 0; //记录下保留路径的起点

for （int j = 0; j 《 statRow; j++） { //遍历J-1时刻的状态

int l=0;

for （int jj = 0; jj 《 outnum*innum; jj++） { //遍历当前段的每个字符来计算路径距离

if （stat［j］［i］ 《 0） { //若两个状态本来就无转移关系，则将l设为无穷大，这样这条路径就不可能被选择了

l = 100;

break;

}

if （curSeq［jj］ ！= out［j］［i］［jj］） //计算汉明距离

l++;

}

if （（u［J - 1］［j］ + l） 《 min） { min = u［J - 1］［j］ + l; minj = j; } //选出累计路径长度最小的

}

u［J］［i］ = min; //将最小的累计路径赋给J时刻的i状态

for （int ii = 0; ii 《 （J - 1） *outnum* innum; ii++） {

BB［i］［ii］ = BB［minj］［ii］;

}

for （int jj = 0; jj 《 outnum*innum; jj++） {

BB［i］［（J - 1）*outnum*innum + jj］ = out［minj］［i］［jj］;

}

//上面两个for循环实现从状态minj继承纠正序列，再往上面填上对应于当前段的纠正段

for （int ii = 0; ii 《 （J - 1） * innum; ii++） {

B［i］［ii］ = B［minj］［ii］;

}

for （int jj = 0; jj 《 innum; jj++） {

B［i］［（J - 1）*innum + jj］ = stat［minj］［i］;

}

//尾加对应于纠正段的输入段，原理同上

}

}

for （int i = 0; i 《 seqLen/outnum; i++） {

res［i］ = B［0］［i］;

}

for （int i = 0; i 《 seqLen; i++） {

fixed［i］ = BB［0］［i］;

}

//赋值给res和fixed

return 1;

}

结语

关于 Vertibi算法的卷积码解码设计应用介绍就到这了，如有不足之处欢迎指正。

相关阅读推荐：什么是卷积码

相关阅读推荐：什么是卷积