浅谈卷积编码在通信中的应用 详解卷积编码设计应用

本文主要是关于卷积编码的相关应用介绍，并着重阐述了卷积编码在通信当中的应用案例。

卷积码

若以（n，k，m）来描述卷积码，其中k为每次输入到卷积编码器的bit数，n为每个k元组码字对应的卷积码输出n元组码字，m为编码存储度，也就是卷积编码器的k元组的级数，称m+1= K为编码约束度m称为约束长度。卷积码将k元组输入码元编成n元组输出码元，但k和n通常很小，特别适合以串行形式进行传输，时延小。与分组码不同，卷积码编码生成的n元组元不仅与当前输入的k元组有关，还与前面m-1个输入的k元组有关，编码过程中互相关联的码元个数为n*m。卷积码的纠错性能随m的增加而增大，而差错率随N的增加而指数下降。在编码器复杂性相同的情况下，卷积码的性能优于分组码。

卷积码的纠错能力不仅与约束长度有关，还与采用的译码方式有关。总之，由于n，k较小，且利用了各组之间的相关性，在同样的码率和设备的复杂性条件下，无论理论上还是实践上都证明：卷积码的性能至少不比分组码差。

卷积编码在通信中的应用

基本概念 

要理解卷积首先要明白脉冲信号和脉冲响应的概念，在线性时不变系统中任意一个信号都可以分解为一组脉冲（impulse）信号的组合。而脉冲信号是一个只是为了分析实际并不存在的信号，其定义是除了某一时间点处有值其他时间点都为0的信号。单位脉冲信号也叫做delta函数即幅度归一化为1，采样点0处为1其他点为0的信号。脉冲信号可以理解为单位脉冲信号经过量化和移位的结果。实际上脉冲分解提供了一种每次只分析一个采样点的方法。当单位脉冲为输入时系统输出信号即为脉冲响应。 

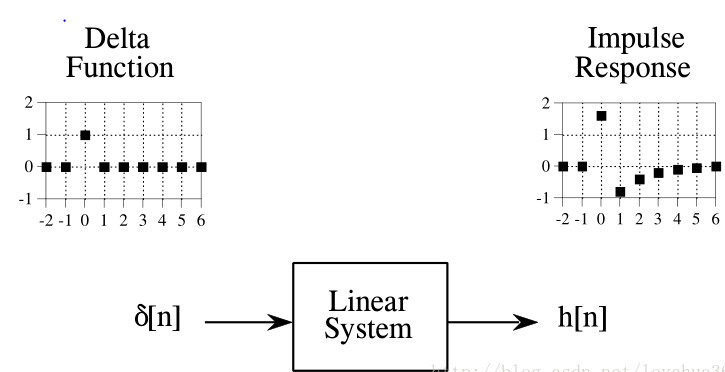
在线性系统里，卷积用来描述输入信号，脉冲响应和输出信号的关系。 

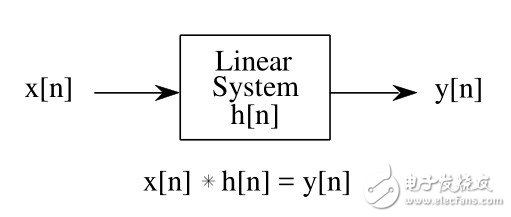
下图中卷积实现低通滤波和高通滤波。 

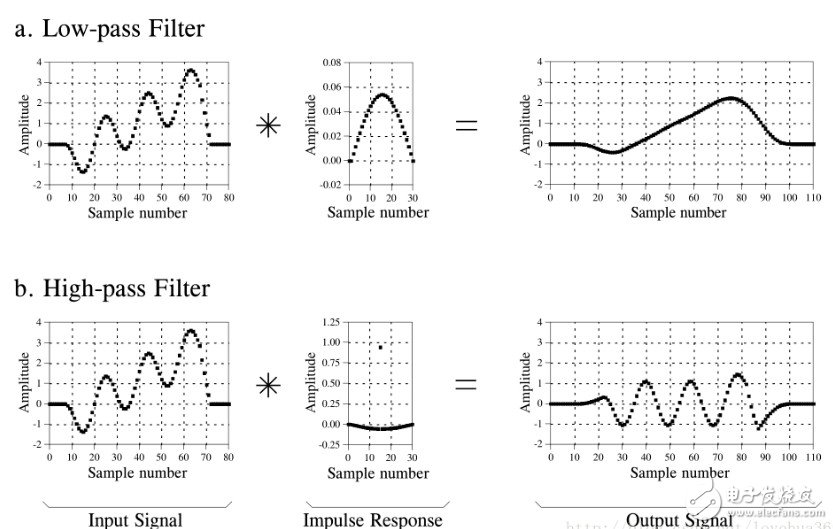
接下来详述卷积的数学描述，可以分别通过输入信号和输出信号的角度看待卷积。

输入信号角度看待卷积

首先从输入信号角度，要看每个输入采样点对输出信号的贡献是什么。如下图所示一个9个输入点的信号通过有4个采样点脉冲响应的系统，其框图如下。

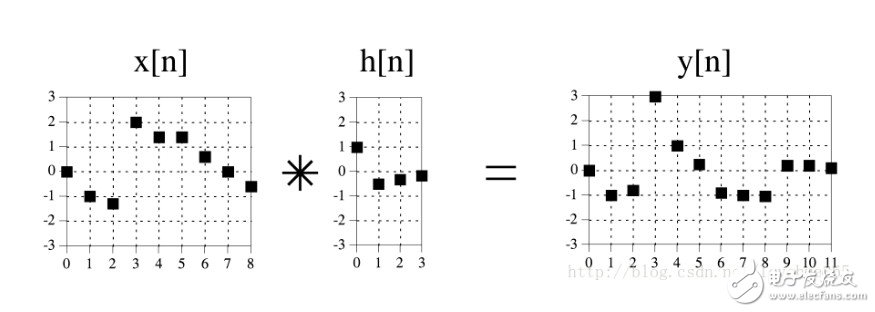
从每一个输入信号采样点的角度来看，其输出即为单位脉冲响应乘以一个系数并移位的结果，所以下图显示了所有9个采样点经过系统的结果。 

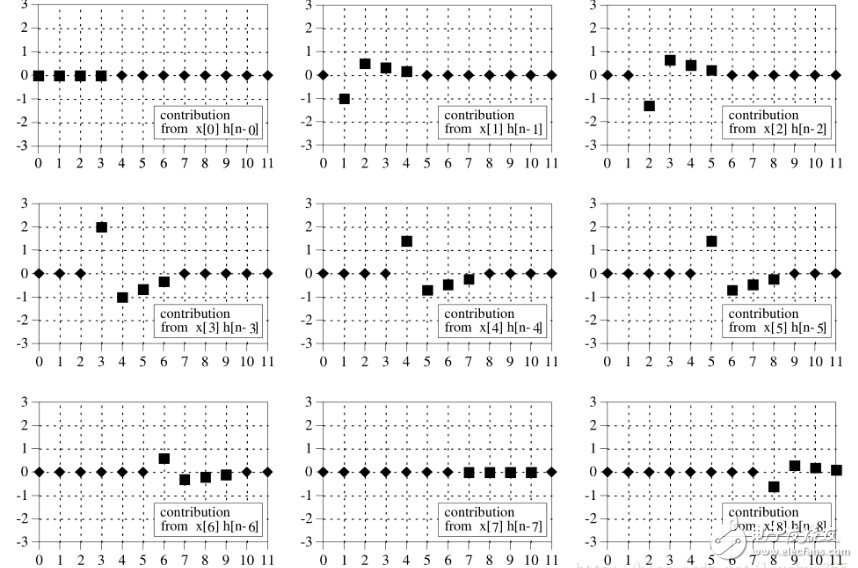
因此可以由此得到9个采样点经过系统之后的输出。卷积还有一个特性就是两个输入可交换，即a*b=b*a。将上例两个输入交换即对于一个4个输入信号通过9个采样点脉冲响应系统的分析如下： 

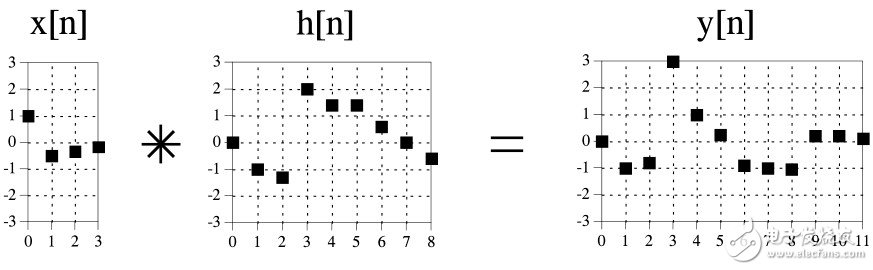
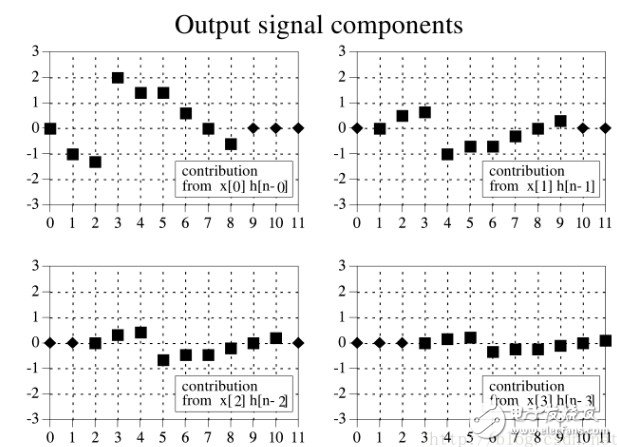
对于从输入信号角度看待卷积，其程序如下所示： 

其核心在于第240行，举例来说，对于输入信号第40个采样点，内部循环每个点通过脉冲响应所做的三件事，首先，脉冲响应被乘以一个输入采样值来进行量化。其次，量化脉冲向右移位40个采样点。最后，输出值累加每个输入采样点产生的结果。

输出信号角度看待卷积

输入信号角度看待卷积输入的每个采样点影响了输出信号的多个采样。在第二种观点，我们反过来单独看输出信号的每个采样点由哪些输入信号采样点产生。假设想要找出给定一些输入信号和脉冲响应的卷积输出，最直观的方法就是计算输出信号每个采样点的输出。这就需要知道如何计算输出信号每个采样点的结果。假设对于y（6）找出哪些输入影响着y（6）的结果。通过看上面所有9个输入采样点经过系统的结果图，可以看出x（3），x（4），x（5），x（6）通过脉冲响应的输出分量影响y（6）。

y（6）=x（3）h（3）+x（4）h（2）+x（5）h（1）+x（6）h（0）

下图将输出端算法阐述为卷积器，流程图显示了如何进行卷积。

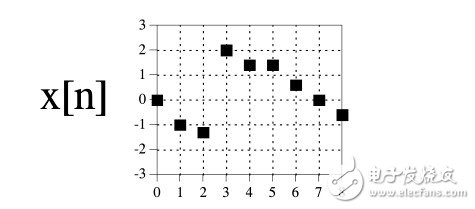
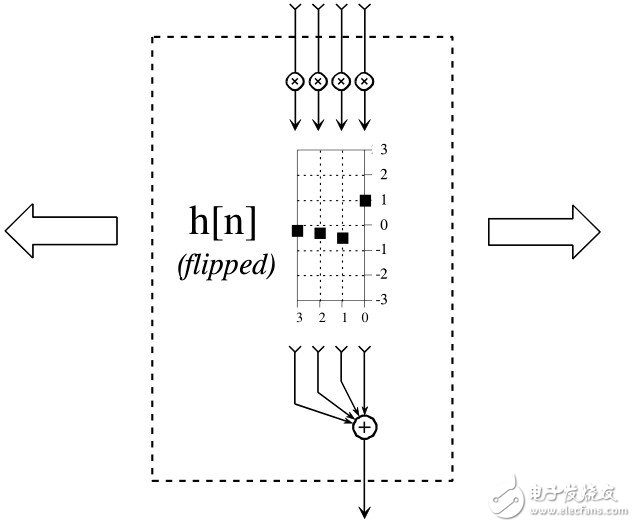
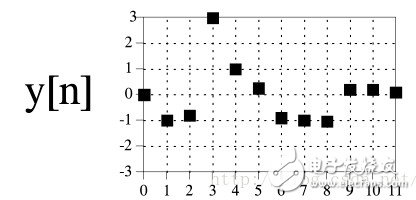
卷积器可以看作黑盒子可以左右进行移动，4个输入信号采样点进入输入端，这些值乘以脉冲响应代表的值并且结果相加。例如y(6)就由x(3),x(4),x(5),x(6)计算出来的。为了计算y(7)，卷积器向右移动一位，另外4个输入x(4)-x(7)进入卷积器。这个过程对于所有需要计算输出信号的点重复进行。 

上图中卷积器中脉冲响应左右移位，进行移位只是简单的数学计算方便。脉冲响应描述了每个输入信号点如何影响输出信号。输出信号每个点的结果由输入信号乘以一个翻转的脉冲响应来影响。 

下图显示了边界处理情况。 

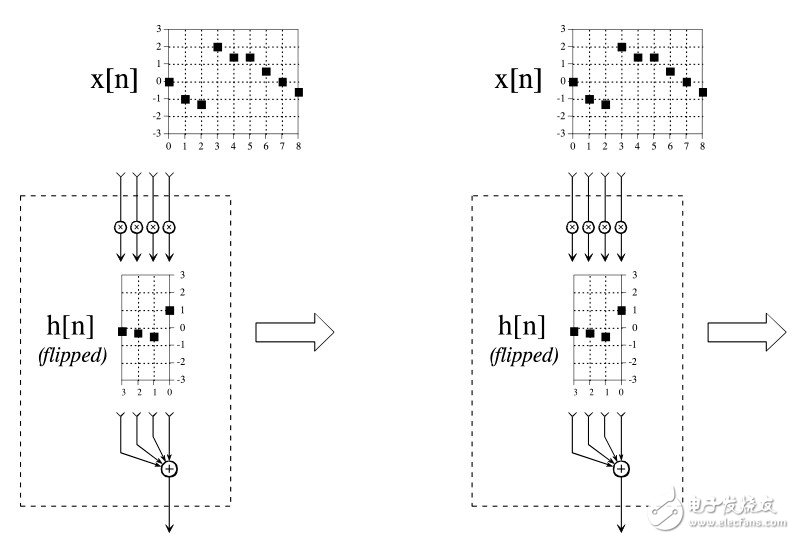
计算y(0)时需要x(-3),x(-2),x(-1)和x(0)，但x(-3),x(-2),x(-1)并不存在。这种情况通过边界加0来处理。 

这种输出信号基于不完整信息的情况在DSP术语中是脉冲响应不完全沉浸在输入信号中。如果脉冲响应长度为M个点，那么输出信号中的第一个到第M-1个采样点是基于不完全输入信息的。这类似于电子电路，需要一定的时间来稳定电源应用。不同的是，这种瞬态在电子学中很容易被忽略，但在DSP中却非常显著。 

下图显示了这种效应带来的麻烦，输入信号是正弦波加上一个DC分量,期望移除信号的DC部分。 

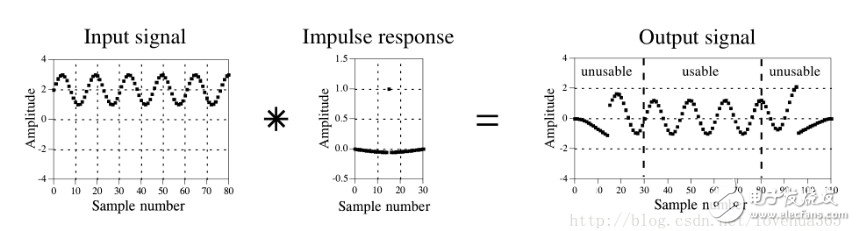
如图所示，前后30个信号出现问题，在DSP中这种“end effect”问题很普遍。因此一般规则是在处理信号时最开始和结束的一些采样点被丢掉不用。 

接下来是卷积的数学公式：

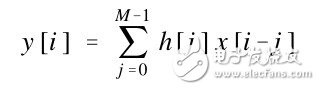
公式中允许输出信号样点逐个计算。为了计算某个输出采样，指数j从0到M-1进行遍历，每个脉冲响应采样点h[j]与适当的输入采样信号x[x-j]相乘之后相加。 
同样的执行卷积的程序如下所示： 

与输入端程序遍历输入采样点不同的是输出端程序遍历输出信号采样点。值得注意的是对于只有80个输入采样点的信号输出信号定义有几种方法。例如扩展输入采样点在边界加0或者是只处理从30到80的信号。

权重输入之和 

通过以上两种分析都可以得到卷积的结果。回头看上边的卷积机器，将脉冲响应考虑为一组权重系数，在这种观点下每个输出信号采样点等于权重输入之和。每个输出采样点由哪些输入信号采样影响取决于权重系数的选取。

结语

关于卷积编码的相关介绍就到这了，如有不足之处欢迎指正。

相关阅读推荐：什么是卷积码

相关阅读推荐：卷积编码是什么