咬尾卷积编码是什么？如何实现咬尾卷积编码？

　　本文主要是关于咬尾卷积编码的相关介绍，并着重阐述了咬尾卷积编码实现的方法。

　　咬尾卷积编码

　　咬尾卷积码，短码。

　　到了4G时代，中国通讯企业慢慢开始有点进步了，TD-LTE技术的突破，使得中国通信技术第一次在世界上有了话语权。但是差距是硬伤，虽然规模已经有了，但是在通信上的核心技术却依旧不能自主研发。依旧依靠引进国外的核心技术，核心长码编码Turbo码和短码咬尾卷积码，都不是中国原创的技术。

　　原理

　　1、咬尾卷积码的原理是尾卷积码保证格形起始和终止于某个相同的状态。它具有不要求传输任何额外比特的优点。Viterbi译码器受格形状态概率和分支度量的约束。传输的数据通常由一串0比特结尾，以强制编码器回到0状态，这样泽码器能从已知的状态开始译码，但是信道必须传输额外的符号。

　　咬尾卷积码的约束长度为7，编码率为1/3。卷积码的编码器配置如图l所示。编码器的移位寄存器的初始值应当没置为输入流的最后6位信息比特，这样移位寄存器的初始和最终状态保持一致。若用S0，S1，S2，。..，S5表示编码器的6个移位寄存器，则移位寄存器的初始值应当设置为：Si=Ck（k一1一i），编码输出流d［0］，d［1］，d［2］分别对应于第l、第2和第3个比特 。

　　2、咬尾技术具有以下优点：

　　●不影响编码率，总的传输比特为N/R;

　　●不影响卷积码的错误校验属性。

　　这项技术也有以下缺点：

　　●泽码延迟增加了，因为必须确定正确的起始

　　状态和回溯的初始状态;

　　●接收器复杂度略微增加。

　　咬尾卷积编码的应用

　　咬尾卷积码优缺点：克服了码率损失的问题，并且适合迭代译码，但是译码复杂度增加了。

　　通常卷积码编码器开始工作时都要进行初始化，常常将编码器的所有寄存器单元都进行清零处理。而在编码结束时，还要使用尾比特进行归零的结尾操作（Tailed Termination）。相对于编码比特而言，尾比特增加了编码开销。

　　TD-LTE系统的卷积码编码器采用了咬尾编码方法，如图1所示，编码器开始工作时要进行特殊的初始化，将输入信息比特的最后m个比特依次输入编码器的寄存器中，当编码结束时，编码器的结束状态与初始状态相同。由于这个编码方法没有出现尾比特，因此称为咬尾编码。咬尾编码减少了尾比特的编码开销。对于咬尾编码方法，在译码过程中，由于编码器的初始状态和结尾状态是未知的，因此就需要增加一定的译码复杂度，才能确保好的译码性能。

　　LTE TS36.212中规定了使用的咬尾卷积编码的约束长度为7，码率为1/3。

　　

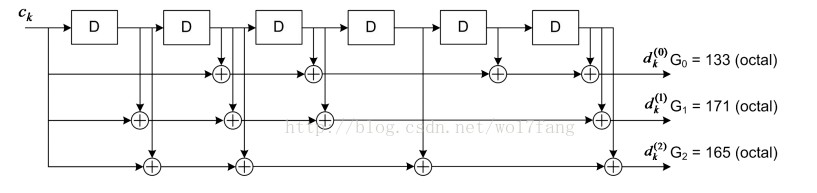
　　其中

　　约束长度：（constraint length）= 寄存器个数（N）+1，即能输出信号到加法器的点的和。

　　编码速率：若以（k，n，m）来描述卷积码，其中k为每次输入到卷积编码器的bit数，n为每个k元组码字对应的卷积码输出n元组码字，m称为约束长度，编码速率k/n。而这里一路输入有三路输出，还不用额外的尾比特。码率自然是1/3。

　　图1中D从左到右分别对应标准上的S0，S1，。。。S5。

　　初始化时，S0=Ck-1，S1=Ck-2，。。。，S5=Ck-6。　　//initialization

　　输入第一个比特C0，d0=C0⊕Ck-2⊕Ck-3⊕Ck-5⊕Ck-6， //⊕代表异或

　　d1，d2同样的方法生成。 　　　　　　　　　　　　　　　　//

　　当输入第二个比特C1时，寄存器右移一位，最末位抛弃，即S5抛弃，第一位变为输入位，即S0=C0。　　//registered update

　　当最后的比特Ck-1进行编码完成后，寄存器又回到了初始状态，就像一条蛇咬住了自己的尾巴，这就是tailbiting的由来。因此，这个卷积码也叫做咬尾卷积码。

　　G0，G1，G2是生成公式，与输入比特异或的寄存器为1，不异或的寄存器为0，因此，第一个输出d0的生成公式是011011，同CRC的生成公式一样，最高位要置1，因此生成公式为1011011。

　　咬尾卷积译码：

　　咬尾卷积译码算法有以下几种：较早提出的Bar-David算法和最大似然算法，后来提出的循环维特比算法（CVA），还有基于该算法的地复杂度的改进算法，如环绕维特比算法（WAVA），双向维特比算法（BVA），还有两步维特比算法、双回溯循环维特比译码算法。

　　如何实现咬尾卷积编码

　　%编码器输入48比特

　　signal = randi（［0 1］，1，48）;

　　fprintf（‘信号长度%d\n’，length（signal））;

　　%1/2咬尾卷积码：先输入尾部的码6比特，再输入正常码48

　　c = ［signal（end-（constLen-2）：end）， signal］;

　　fprintf（‘补充尾部后信号长度%d\n’，length（c））;

　　%打孔器设计

　　%信号的长度必须是打孔向量长度的整数倍

　　%打孔长度本来为24*4 = 96比特，但是由于信号多输入了6比特，会多产生12比特，所以打孔向量的长度为96+12=108

　　%这12比特需要被被完全打掉

　　p = ［1 1 ;1 0］;

　　p =reshape（p，1，4）;

　　for i = 1:23

　　p = ［p，1 1 1 0］;

　　end

　　%前面补0是为了打孔时，将前面的尾部生成的比特打掉（尾部本来是应该放在初始状态中的）

　　p = ［zeros（1，12），p］;

　　fprintf（‘打孔器的长度为 %d\n’，length（p））

　　% 卷积编码

　　C = convenc（c， convCode，p）;

　　fprintf（‘卷积编码输出长度为 %d\n’，length（C））

　　%解码部分

　　tbLen = length（C）/rateInv;

　　%为了能在译码时获得咬尾卷积码的初始状态，把接收到的码子拷贝两份译码，第一份译码完毕以后，编码器的状态就与咬尾卷积码的起始状态相同了

　　C = ［C，C］;

　　fprintf（‘双份比特的长度为%d\n’，length（C））%144

　　%相应的，解码器的打孔矩阵也要发生变化：

　　%当数据重复2份时，解码时的打孔矩阵并不是将原先的打孔矩阵重复而是，将编码打孔时的用来打掉咬尾的打孔部分去掉

　　p = ［p（1+12:end），p（1+12:end）］;

　　%输入解码器的比特长度应该是打孔矩阵的1的个数的整数倍

　　fprintf（‘打孔矩阵1的个数为%d\n’，sum（p））

　　%译码

　　cR = vitdec（C， convCode， tbLen， ‘trunc’， ‘hard’，p）;

　　fprintf（‘译码输出个数为%d\n’，length（cR））;

　　%解码时选择后面那一份的译码结果

　　recv = cR（length（cR）/2+1:end）;

　　fprintf（‘最终结果个数为%d\n’，length（recv））;

　　err = sum（abs（recv-signal））

　　结语

　　关于咬尾卷积编码的相关介绍就到这了，希望通过本文能让你对咬尾卷积编码有更深的了解。