浅谈卷积编码在DSL中的应用 详解卷积编码编码技术

　　本文主要是关于卷积编码的相关介绍，并着重探讨了卷积编码在DSL中的应用功效。

　　卷积编码

　　卷积码是一种差错控制编码，由P.Elias于1955年发明。因为数据与二进制多项式滑动相关故称卷积码。卷积码在通信系统中应用广泛，如IS-95，TD-SCDMA，WCDMA，IEEE 802.11及卫星等系统中均使用了卷积码。

　　

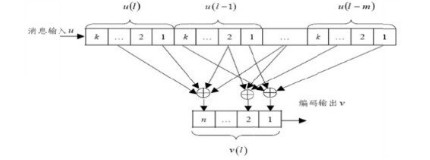
　　卷积码使用（n，k，L）表示，码率为R。

　　n为输出码字；

　　k为输入的比特信息；

　　L为约束长度，也称为记忆深度。

　　R表示为R = k/n。

　　卷积码是一种有记忆的纠错码，编码规则是将k个信息比特编码形成n个比特，编码后的n个码元不但与当前输入的k个信息有关，仍与之前的L-1组的信息有关。

　　卷积编码编码技术

　　在卷积码的编码过程中，对输入信息比特进行分组编码，每个码组的编码输出比特不仅与该分组的信息比特有关，还与前面时刻的其他分组的信息比特有关。同样，在卷积码的译码过程中，不仅从当前时刻收到的分组中获取译码信息，还要从前后关联的分组中提取相关信息。正是由于在卷积码的编码过程中充分利用了各组的相关性，使得卷积码具有相当好的性能增益。

　　编码器图中，编码器的每组输入包含k0个信息比特，第一组寄存器单元存储当前时刻的k0个信息比特，而其他组寄存器单元存储前面时刻的（K−1）k0个信息比特。编码器有n0个编码输出，每个编码输出Yi由当前时刻的输入信息分组以及其他（K−1）个寄存器单元内的信息分组根据相应的连接关系进行模2运算来确定。

　　因此，一般定义K为编码约束度，说明编码过程中相互关联的分组个数，定义 m=k-1 为编码存储级数，码率 R=k0/n0，这类码通常称为（n0，k0，K）卷积码。在许多实际应用场合，往往采用编码约束度比较小、码率为的卷积码。如图3-29所示的两种卷积码（2，1，9）和（3，1，9），它们的存储级数都是8，加法器完成二进制加法（模2加）。图中省略了存储当前时刻输入的寄存器单元。在图3-29（a）中，（2，1，9）卷积码编码器有一个输入端口、两个输出端口，这两个输出端口分别对应两个生成多项式（使用八进制表示）：561和753。该码率是1/2。在图3-29（b）中，（3，1，9）卷积码编码器有一个输入端口、3个输出端口，这3个输出端口分别对应3个生成多项式（使用八进制表示）：557、663和711。该码率是1/3。

　　TD-LTE系统中采用了（3，1，7）卷积码，存储级数是6，使用了6个寄存器。这个卷积码的主要优点包括最优距离谱、咬尾编码、译码复杂度小。具体描述见后续章节内容。另外，卷积码也可以按照其他方式进行分类，比如系统码或者非系统码，递归码或者非递归码，最大自由距离码或者最优距离谱码。常用的卷积码一般是非递归的非系统码，而Turbo码常常使用递归的系统卷积码。

　　咬尾编码通常卷积码编码器开始工作时都要进行初始化，常常将编码器的所有寄存器单元都进行清零处理。而在编码结束时，还要使用尾比特进行归零的结尾操作（Tailed Termination）。相对于编码比特而言，尾比特增加了编码开销。TD-LTE系统的卷积码编码器采用了咬尾编码方法。

　　编码器开始工作时要进行特殊的初始化，将输入信息比特的最后m个比特依次输入编码器的寄存器中，当编码结束时，编码器的结束状态与初始状态相同。由于这个编码方法没有出现尾比特，因此称为咬尾编码。咬尾编码减少了尾比特的编码开销。对于咬尾编码方法，在译码过程中，由于编码器的初始状态和结尾状态是未知的，因此就需要增加一定的译码复杂度，才能确保好的译码性能。3．性能界卷积码的性能一般使用误比特率（BER，Bit Error Rate）来统计，其理论上界（Upper Bound）一般使用联合界（Union Bound）来确定，即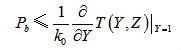（3-13）其中，卷积码的转移函数（Transfer Function），代表非零输入信息比特的转移分支，Y的指数表示输入信息比特的汉明重量，Z代表输出编码比特的转移分支，Z的指数表示输出编码比特的汉明重量。为了进一步分析上述性能界，一般假设最大似然译码（ML，Maximum-Likelihood）、BPSK调制和加性高斯白噪声（AWGN，Additive White Gaussian Noise）信道，则有

　　

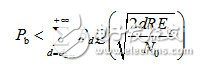
　　（3-14）其中，Bd是所有重量为d的码字的非零信息比特的重量，为卷积码的自由距离。当信噪比很高时，则式（3-14）近似为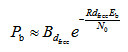（3-15）BPSK调制性能为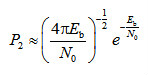（3-16）考虑到误码性能主要是指数项占据主导作用，与未编码系统相比，卷积码的编码增益为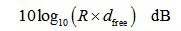（3-17）式（3-17）说明卷积码的渐近性能主要是由自由距离（）决定的。因此，相对而言，卷积码的自由距离越大，其性能越好。以上述二进制卷积码（2，1，9）和（3，1，9）为例，自由距离分别为12和18，编码增益都为7.78dB。实际上，性能最佳的卷积码往往具有最优的距离谱（ODS，Optimum Distance Spectrum）或者重量分布，而且，具有最优距离谱的卷积码也具有最大的自由距离（MFD，Maximum Free Distance）。TD-LTE系统采用了最优距离谱的卷积码。

　　卷积编码在DSL中的应用

　　随着Internet技术的不断发展，人们对传输数据的速度、质量要求越来越高，在当前为了有效地利用现有的资源——电话线，提出了DSL〔1〕（数字用户线）的概念，使用话音频率以上的频带（4 k~1.1 MHz）来调制高速数字信号，按照Δf=4.3125 kHz分割成一个个的子带，由于Δf刚好是音频的宽度，故命名为离散多音频，DMT调制是基于离散傅立叶变换对并行数据进行调制解调的。随着超大规模集成电路（VL SI）和数字信号处理（DSP）技术的不断进步，用FFT实现实时DMT调制已付诸使用。

　　但以往的调制解调系统，纠错编码与调制是各自独立设计并实现的，译码和解调也是如此，这样解调器在接收信号是对信号作独立硬判决，硬判决结果再送给译码器译码，这种硬判决会导致接收端信息的不可恢复的丢失，解决这个问题的方法是在接收端采用软判决译码。DSL技术中就是将DMT和网格编码综合设计，在白噪声环境下比传统技术的误码性能有了很大的提高。这种最佳的编码调制系统是按照编码序列的欧氏距离为设计的量度，这就要求将编码器和调制器当作一个统一的整体进行综合设计，使得编码器和调制器级联后产生的编码信号序列具有最大的欧氏自由距离。从信号空间的角度看，这种最佳编码调制的设计实际上是一种对信号空间的最佳分割。经过实验分析，DMT和卷积编码结合后的编码增益比传统编码的编码增益增加了8 dB。？

　　接入设备体系结构

　　在ADSL的应用当中，其硬件体系结构大致是由线路接口、接收滤波、线路驱动、模拟前端以及DMT收发器这几个模块组成。其中DMT收发器在发端对数据进行复用、循环冗余校验、前向纠错、子带排序、卷积编码、星座映射以及IFFT变换，送到模拟前端变换成模拟信号发送出去，而在收端是将模拟信号经过FFT变换、解映射、维特比译码等一系列反变换，提交给上层。根据T1.413〔4〕标准，采用韦氏16状态4维网格码作为内码，采用Reed？Solomon编码作为前向纠错码，另外由于网格编码对成块的噪声抵抗能力较差，因此在进行网格编码之前将数据进行交织使噪声分散。ADSL的DMT收发器框图大致如图1所示。

　　DMT与卷积编码调制原理

　　在ADSL的发送端，将数据分配到不同的子带上，这种分配可以根据各个子带的信噪比来确定分配的bit数。而ADSL系统为各个子带建立并维持了一个比特数和增益大小的表，是在ATU-R一端计算出来并返回给局端。为保证后一子带所带的位数不小于前一子带的位数，先对子带进行排序，即子带按信噪比大小从小到大进行排序。为了使编码获得的码字有较大的欧氏自由距离，采用了四维TCM网格编码，这样位抽取是基于一对子带的，因为一个子带在空间上是二维的，一对相互正交的子带在空间上则是四维的 ，相应的在解码的时候也是一对一对的作维特比译码。欧氏自由距离是在四维空间上计算出来的，这样四维的陪集可以由两个二维的陪集的联合构成，即这样四维TCM网格码的欧氏自由距离可以由两个二维星座图的距离的平方和算出， 在译码系统中，最可能发生错误的情况是在具有最小的平方欧氏距离的两个序列？{an}和{bn}？之间，（前者是发送序列，后者是译码序列），这一最小平方欧氏距离常又称为平方自由距离，记做：

　　编码的目的是为了使这个平方自由距离最大。

　　网格编码调制的通过一种特殊的信号映射可变成卷积码的形式。这种映射的原理是将调制信号集分

　　割成子集，是的子集内的信号间具有更大的空间距离，用编码效率为k/（k+1）的卷积码选择子集，用其余位选择子集中的点。在DSL数字用户环路中用16状态的4维网格编码的编码器结构。

　　每两个子带抽取的位数z′=x+y-1（x为第一个子带所带的位数，y为第二个子带所带的位数）。{uz′-1，uz′-2，…u1}为原码，输出的是经过卷积以及异或以后的编码，为两个二进制码字，即{vz-y？，vz′-y-1，…v1，v0}和{wy-1，wy-2，…w1，w0}，这两个二进制码字将映射成两个星座点。编码算法使星座点的两个最低位决定星座点的二维陪集{v1，v0}和{w1，w0}实际上是这个上标的二进制表示。对于一帧中最后两个码字，为了使卷积编码状态{s3，s2，s1，s0}回到零状态。让编码前的码字的{u1，u2}={0，0}，则最后两对子带抽取的位数z′＝x+y-3。

　　这样编码得出的信号有两个基本特征：

　　（1）星座图中所用的信号点数大于未编码同种调制所需的点数（扩大了一倍），这些附加的信号点为纠错编码提供冗余度。

　　（2）采用卷积码在相继的信号点之间引入某种依赖性，因而只有某些信号点序列才是允许出现的，这些允许的信号序列可以模型化为网络结构。可用网格图来表述。

　　在接收端对接收序列进行维特比译码〔4〕，即最大似然译码，可以用网格图求最相似的路径来描述这种算法，它依赖于有限状态的马尔可夫系统的描述，包括状态变迁以及状态变迁的输出码字。在四维TCM？编码的基础上，解码时要对一对一对的数据进行解码，计算码距时也是以四维空间的欧氏距离为标准，取最相似的一条路径。对于长度为L+m的网格路径（L为信息序列的长度，m表示后缀为m个0向量）接收序列为所有的网格路径在零时刻发散于同一个初始状态、收敛于第j时刻（j＝L+ m）的同一个最后一状态。在理想状况下，对于一个存储量无限度的通道，可以将所有可能的路径都记录下来，然后选择其中对数似然函数值最大的作为译码结果。

　　对数似然函数是将接收序列判定为某条路径的序列的条件概率的对数

　　这里的对数似然函数取最大值，实际上是接收的码序列与估计路径的码之间的距离取最小值，是基于欧氏空间距离来计算的。在这里维特比译码算法的核心是回退的观点，采用动态规划法存储数据，如果对每条可能的路径进行存储的话，随着译码深度的增加，存储量将成4的指数增长，这在现实条件下是不可能的。因为每个节点都有四个分支（二输入十六状态的网格图），因此我们对于j时刻到达的某一状态

　　i（i=1，2…，S-1），进行加—比—选操作，即将所有可能前一时刻的状态的最大似然函数∧j-1（δp）与当前接收的序列和前一状态到当前状态的估计码的似然度相加，选择其中最大的作为j时刻i状态的最大似然函数值，并在幸存序列j（δi）在原来的基础上加上这条最优的路径u〔δp→δi〕。这样给出的算法可以表述为：

　　变量／存储

　　结语

　　关于卷积编码的相关介绍就到这了，如有不足之处欢迎指正。

相关阅读推荐：基于VHDL的卷积编码实现

相关阅读推荐：什么是卷积码