

卷积码的约束长度是多少?如何计算?
编码与解码
描述
本文主要是关于卷积码的相关介绍,并着重阐述了卷积码的约束长度及其计算方法。
卷积码
卷积码将k个信息比特编成n个比特,但k和n通常很小,特别适合以串行形式进行传输,时延小。
若以(n,k,m)来描述卷积码,其中k为每次输入到卷积编码器的bit数,n为每个k元组码字对应的卷积码输出n元组码字,m为编码存储度,也就是卷积编码器的k元组的级数,称m+1= K为编码约束度m称为约束长度。卷积码将k元组输入码元编成n元组输出码元,但k和n通常很小,特别适合以串行形式进行 传输,时延小。与分组码不同,卷积码编码生成的n元组元不仅与当前输入的k元组有关,还与前面m-1个输入的k元组有关,编码过程中互相关联的码元个数为n*m。卷积码的纠错性能随m的增加而增大,而差错率随N的增加而指数下降。在编码器复杂性相同的情况下,卷积码的性能优于分组码。
卷积码(n,k,m) 主要用来纠随机错误,它的码元与前后码元有一定的约束关系,编码复杂度可用编码约束长度m*n来表示。一般地,最小距离d表明了卷积码在连续m段以内的距离特性,
该码 可以在m个连续码流内纠正(d-1)/2(向下取整)个错误。
1955 年Elias 发明了卷积码。它也是将k 个信息元编成n 个码元,但k 和n 通常很小,特别适合以串行形式进行传输,时延小。与分组码不同,卷积码编码后的n 个码元不仅与当前段的k 个信息元有关,还与前面的N ?1段信息有关,各码字间不再是相互独立的,码字中互相关联的码元个数为n 。
N 。同样,在译码过程中不仅从此时刻收到的码元中提取译码信息,而且还利用以后若干时刻收到的码字提供有关信息。卷积码的纠错性能随k 的增加而增大,而差错率随N 的增加而指数下降。
由于卷积码的编码过程充分利用了码字间的相关性,因此在码率和复杂性相同的条件下,卷积码的性能优于分组码。但卷积码没有分组码那样严密的数学结构和数学分析手段,目前大多是通过计算机进行好码的搜索。
卷积码的约束长度是多少
二进制卷积码编码器的形式如下图所示,它包括一个由N 个段组成的输入移位寄存器,每段有k 个寄存器;一组n 个模2 相加器和一个n 级输出移位寄存器。对应于每段k 个比特的输入序列,输出n 个比特。由图中可以关,还与前(N ?1) ? k 个输入信息有关。整个编码过程可以看成是输入信息序列与由移位寄存器和模2 相加器的连接方式决定的另一个序列的卷积,因此称为“卷积码”。我们通常将N称为卷积码的约束长度,并把卷积码记为: (n, k, N) 。其码率也为Rc =k/n 。非二进制卷积码的形式很容易以此类推。
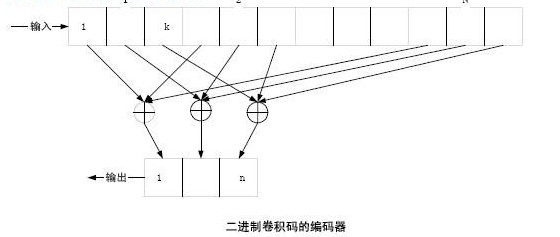
卷积码的描述方式分为解析法和图解法两类。解析法包括矩阵形式和生成多项式形式,图解法包括树图、状态图和网格图。
结构图
多项式法就是由卷积码的生成多项式直接得出其编码器的结构图。如前面卷积码状态图例子中的(2,1,2)卷积码的生成多项式矩阵为:G(D)=[1 ,1 ]其中,D是延迟算子,生成多项式的第一项为1 D ,表示输出编码的第一个码元等于输入码元x(n)与前两个时刻输入的码元x(n-1)、x(n-2)的模2和,同理第二项类似。
编码器
由图所示,随着信息序列不断输入,编码器就不断从一个状态转移到另一个状态并同时输出相应的码序列,所以图3所示状态图可以简单直观的描述编码器的编码过程。因此通网格图过状态图 很容易给出输入信息序列的编码结果,假定输入序列为110100,首先从零状态开始即图示a状态,由于输入信息为“1”,所以下一状态为b并输出“11”,继续输入信息“1”,由图知下一状态为d、输出“01”……其它输入信息依次类推,按照状态转移路径a-》b-》d-》c-》b-》c-》a输出其对应的编码结果“110101001011”。

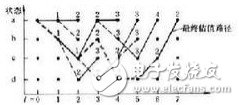
网格图 状态图可以完整的描述编码器的工作过程,但是其只能显示状态转移的过程而不能显示状态转移发生的时刻,由此引出用来表示卷积码的另一种常用方法——网格图。网格图就是时 间与对应状态的转移图(如图),在网格图中每一个点表示该时刻的状态,状态之间的连线表示状态转移。
通过观察网格图可以发现在网格图中输入信息x(n)并没有标出,但如观察到转移后的状态表示(x(n),维特比译码过程x(n-1))就可以发现输入信息已经隐含在转移后的状态中。在图中还可以发现两个网格图不同主要集中在转移后状态位置不同。重新排序结构(即所谓蝶型结构)是为了优化运算而设计的,因为其中蝶型与蝶型之间是相互独立的。
从上图可以分析得出,如果编码的约束长度不是真实的约束长度,其秩函数的值集中在0-1之间分布,没有出现线性关系。但是编码的约束长度为真实的约束长度的n倍时,秩函数的峰值在图中呈线性关系。由于卷积码是有记忆的,因此在同一个约束长度内是具有相同的线性关系的。
对上图继续进行分析,我们发见,秩函数的峰值均是8的倍数,因此我们可以判断出这段编码的约束长度是8由N=n(m+1)=8计算得出n=2,m=3或n1=4,m=1。显而易见nn=4,m=1是不正确的,所以我们得到正确的编码参数n=2,m=3在确定了正确的编码长度以及约束长度后,我们再通过秩函数的识别方法对编码的起点进行确定。我们选择当秩函数的最大值作为码字的起始位置。对卷积码(2,1,3)起始位置用秩函数的方法进行仿真识别,见图47
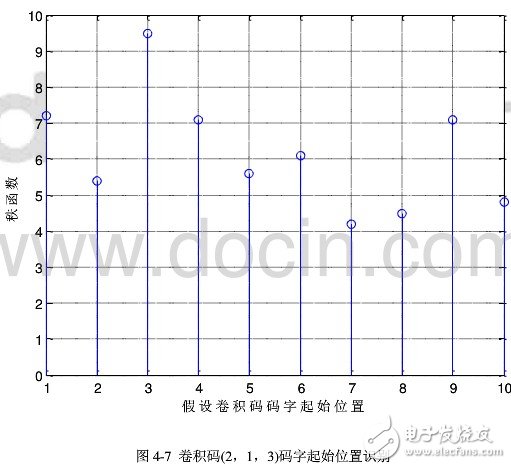
通过秩函数的方法对码字的真实起始位置判别可以显然看出,如果假定的码字的起始位置重合,那么得到的秩函数的值就最大,如果位置不重合或错误,那得到的秩函数的值就必然小于重合位置的值,所以在上图得出的结果中我们可以判定,第三种假设码字序列的起始位置的秩函数的值均不同程度的大于其他假定位置,这里我们就可以得出判断,第三个假设位置即为真实码字的起始位置在通过该算法识别出该卷积码的码长以及码字的起始位置后,我们对上述数据分组组成矩阵,并且以约束长度作为矩阵的一行。
结语
关于的相关介绍就到这了,希望本文能对你有所帮助。
-
回溯长度的大小对卷积码性能有影响吗?2021-06-09 5519
-
在FPGA上实现咬尾卷积码的最优算法设计2019-05-03 6404
-
卷积码编码和维特比译码的原理、性能与仿真分析2018-11-14 14096
-
卷积编码之维特比译码介绍 浅析卷积码之应用2018-08-21 4311
-
FPGA做卷积码的提问2015-04-07 2743
-
基于OCDMA的新型卷积码译码方案2010-08-26 963
-
卷积码,什么是卷积码2010-04-03 7599
-
卷积码,卷积码是什么意思2010-03-19 2193
-
卷积码/Viterbi译码,卷积码/Viterbi译码是什么2010-03-18 2447
-
卷积码的Viterbi高速译码方案2010-01-06 751
-
基于CPLD的卷积码编解码器的设计2009-08-10 3210
-
什么是卷积码? 什么是卷积码的约束长度?2008-05-30 20018
全部0条评论

快来发表一下你的评论吧 !

