

卷积码编码及译码实验 浅谈卷积编码下的FPGA实现
电子说
描述
卷积编码是现代数字通信系统中常见的一种前向纠错码,区别于常规的线性分组码,卷积编码的码字输出不仅与当前时刻的信息符号输入有关,还与之前输入的信息符号有关。
本文主要是关于卷积码编码及译码实验的相关介绍,并着重分析阐述了基于卷积编码下的FPGA实现。
卷积编码
卷积码的编码分为两类:前馈和反馈,在每类中又可分为系统和非系统形式。我们这里只考虑非系统形式的前馈编码器。‘
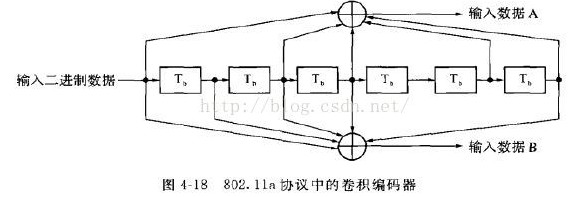
上图是WLAN 802.11a协议中采用的卷积编码器结构,输入比特k=1,输出n=2,存储器长度m=6,编码输出不仅与当前输入有关,还与存储器存储的之前的输入数据有关,具体由之前的哪些数据得到编码输出呢,由生成多项式确定其连接关系。这里,生成多项式为g0=133(八进制)和g1=171(八进制)(右边是最高位),输出数据A的生成多项式为:
输出数据B的生成多项式为:
生成多项式确定了卷积编码器输出的连接关系。根据多项式的系数,在相应项进行连接。生成多项式写成二进制序列的形式分别为:g0 = [1 0 1 1 0 1 1]和g1 = [1 1 1 1 0 0 1](右边是最高位)。我们假设信息序列u,两个编码器输出序列分别为v(0)和v(1),编码器可以看成一个线性系统,系统的信道响应脉冲最多持续m+1个时间单元,编码输出可以写成编码输入与信道脉冲响应的卷积(即生成多项式),即
其中需要注意的是,所有的加法都是模2加运算。
卷积码编码及译码实验
基本原理
1、卷积码编码
卷积码是一种纠错编码,它将输入的k个信息比特编成n个比特输出,特别适合以串行形式进行传输,时延小。卷积码编码器的形式如图17-1所示,它包括:一个由N段组成的输入移位寄存器,每段有k段,共Nk个寄存器;一组n个模2和相加器;一个由n级组成的输出移位寄存器,对应于每段k个比特的输入序列,输出n个比特。
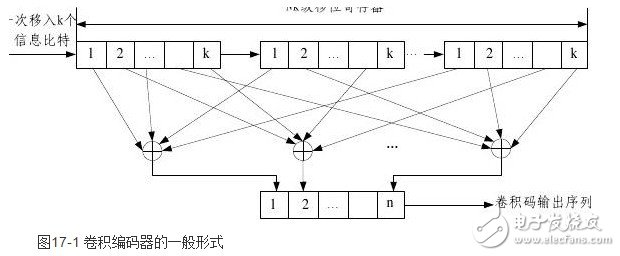
由图17-1可以看到,n个输出比特不仅与当前的k个输入信息有关,还与前(N-1)k个信息有关。通常将N称为约束长度(有的书中也把约束长度定为nN或N-1)。常把卷积码
记为:(n 、k 、N ),当k =1时,N -1就是寄存器的个数。编码效率定义为:
/c R k n = (17-1) 卷积码的表示方法有图解表示法和解析表示法两种:解析法,它可以用数学公式直接表达,包括离散卷积法、生成矩阵法、码生成多项式法;图解表示法,包括树状图、网络图和状态图(最的图形表达形式)三种。一般情况下,解析表示法比较适合于描述编码过程,而图形法比较适合于描述译码。
(1)图解表示法
(2)解析法
下面以(2,1,3)卷积编码器为例详细讲述卷积码的产生原理和表示方法。(2,1,3)卷积码的约束长度为3,编码速率为1/2,编码器的结构如图17-2所示。
j
j
图17-2 (2,1,3)卷积编码器
这里我们主要介绍码多项式法。我们可以用多项式来表示输入序列、输出序列、编码器中移位寄存器与模2和的连接关系。
为了简化,仍以上述(2,1,3)卷积码为例,例如输入序列1011100…可表示为 ()2341M x x x x =++++ (17-2) 在一般情况下,输入序列可表示为
()231234M x m m x m x m x =++++ (17-3) 这里m 1,m 2,m 3,m 4…为二进制表示(1或0)的输入序列。x 称为移位算子或延迟算子,它标志着位置状况。
我们可以用多项式表示移位寄存器各级与模2加的连接关系。若某级寄存器与模2加相连接,则相应多项式项的系数为1;反之,无连接线时的相应多项式项系数为0,以图17-2编码器为例,相应的生成多项式为
()()212211g x x x g x x =++⎧⎪⎨=+⎪⎩ (17-4)
利用生成多项式与输入序列多项式相乘,可以产生输出序列多项式,即得到输出序列。
()()()()()
234211234345245646
1111P x M x g x x x x x x x x x x x x x x x x x x x x ==+++++=+++++++++++=+++
(17-5)
()()()
()()2234211P x M x g x x x x x ==++++ (17-6)
对应的码组为
()()
()()()()461135622121110010111001011,11,10,00,01,10,01,11P x x x x p P x x x x p P p p =+++↔==+++↔===
(17-7)
2、卷积码译码
卷积码的译码方法有两类:一类是大数逻辑译码,又称门限译码;另一类是概率译码,概率译码又能分为维特比译码和序列译码两种。门限译码方法是以分组理论为基础的,其译码设备简单,速度快,但其误码性能要比概率译码法差。这里我们主要介绍维特比译码。
维特比(Viterbi )译码和序列译码都属于概率译码。当卷积码的约束长度不太大时,与序列译码相比,维特比译码器比较简单,计算速度更快。维特比译码算法,以后简称VB 算法。
采用概率译码的一种基本想法是:把已接收序列与所有可能的发送序列做比较,选择其中码距最小的一个序列做为发送序列。如果发送L 组信息比特对于(,)n k 卷积码来说,可能发送的序列有2kL 个,计算机或译码器需存储这些序列并进行比较,以找到码距最小的那个序列。当传信率和信息组数L 较大时,使得译码器难以实现。VB 算法则对上述概率译码(又称最大似然解码)做了简化,以至成为了一种实用化的概率算法。它并不是在网格图上一次比较所有可能的2kL 条路径(序列),而是接收一段,计算和比较一段,选择一段有最大似然可能的码段,从而达到整个码序列是一个有最大似然值的序列。
下面将用图17-2的(2,1,3)卷积码编码器所编出的码为例,来说明维特比解码的方法和运作过程。为了能说明解码过程,这里给出该码的状态图,如图17-5所示。维特比译码需要利用图来说明译码过程。根据前面的画网格的例子,读者可检验和画个该码网格图如图17-4所示。该图设输入信息数目L=5,所以画有L+N=8个时间单位(节点)。这里设编码器从a 状态开始运作。该网格图的每一条路径都对应着不同的输入信息序列。由于所有的可能输入信息序列共有2kL 个,因而网格图中所有可能路径也有2kL 条。这里节
a=00,b=01,c=10,d=11。
设输入编码器的信息序列为(1 1 0 1 1 0 0 0 ),则由编码器输出的序列Y=(1 1 0 1 0 1 0 0 0 1 0 1 1 1 0 0 ),编码器的状态转移路线为abcdbdca。若收到的序列R=(0 1 0 1 0 1 1 0 0 1 0 1 1 1 0 0 ),对照网格图来说明维特比译码的方法。
由于该卷积码的约束长度为6位,因此先选择接收序列的前6位序列
R=(0 1 0 1 0 1)
1
同到达第3时刻可能的8个码序列(即8条路径)进行比较,并计算出码距。该例中到达第3时刻a点的路径序列是(0 0 0 0 0 0)和(1 1 1 0 1 1 ),它们与
R的距离分别是3和4;到
1
达第3时刻b点的路径序列是(0 0 0 0 1 1)和(1 1 1 0 0 0),它们与
R的距离分别是3和4,
1
到达第3时刻c点的路径序列是(0 0 1 1 1 0)和(1 1 0 1 1 0),与
R的距离分别是4和1;
1
到达第3时刻d点的路径序列是(0 0 1 1 0 1)和(1 1 0 1 1 0),与
R的距离分别是2和3。
1
上述每个节点都保留码距较小的路径为幸存路径,所以幸存路径码序列是(0 0 0 0 0 0)、(0 0 0 0 1 1)、(1 1 0 1 0 1)和(0 0 1 1 0 1),如图17-6(a)所示。用与上面类同的方法可以得到第4、5、6、7时刻的幸存路径。需指出对于某一个节点而言比较两条路径与接收序列的累计码距时,若发生两个码距值相等,则可以任选一路径作为幸存路径,此时不会影响最终的译码结果。图17-6(b)给出了第5时刻的幸存路径,读者可自行验证。在码的终了时刻a状态,得到一根幸存路径,如图17-6(c)所示。由此看到译码器输出是‘R=(1 1 0 1 0 1 0 0 0 1 0 1 1 1 0 0),即可变换成序列(1 1 0 1 1 0 0 0),恢复了发端原始信息。比较’R和R序列,可以看到在译码过程中己纠正了在码序列第1和第7位上的差错。当然,差错出现太频繁,以至超出卷积码的纠错能力,则会发生误纠,这是不希望的。
FPGA实现
这里,采用verilog语言对编码过程进行描述。通过状态机控制编码的过程,设置有三种状态:IDLE,ENCODING,CLEAR。通常卷积编码以数据块为单元,逐块进行编码的。当待编码的数据块未到达编码单元时,状态机处于IDLE态,即空闲状态,不做任何处理。当数据块到来时,存在一个触发信号,让状态机开始进入ENCODING状态,即编码状态,编码状态持续的时间为输入的数据块的长度。此外,状态机还设置有CLEAR态,因为在卷积编码中,还有尾比特需要输出,这时输入看做全0输入,存储器逐渐清空,持续时间为尾比特的长度。这一步完成后,状态机重新回到IDLE态,等待下一个数据块的到来。代码如下:
conv_encoder(
input clk,
input rst_n,
input e_start_i, //数据起始信号,比数据uncoded_bits第一个符号早一个时钟,作为编码状态机的启动信号
input uncoded_bits,
output reg e_start_o,
output reg [1:0] coded_bits
);
% 常量定义
parameter UNCODED_BLOCK_LEN = 100; //未编码的数据块长度
parameter CODED_BLOCK_LEN = 106; //编码后的单路数据块长度
% 状态机定义
parameter IDLE = 3‘b001;
parameter ENCODING = 3’b010;
parameter CLEAR = 3‘b100;
reg [2:0] state;
//
reg [7:0] datain_cnt;
reg [5:0] shift_reg;
//
wire encoder_clear_start;
wire encoder_end;
wire encoder_enable;
assign encoder_clear_start = (datain_cnt == UNCODED_BLOCK_LEN -1);
assign encoder_end = (datain_cnt == CODED_BLOCK_LEN -1);
assign encoder_enable = (state != IDLE);
/*********************************************************************/
// 卷积编码状态机
/*********************************************************************/
always @(posedge clk)
begin
if(!rst_n)
state 《= IDLE;
else begin
case(state)
IDLE: state 《= e_start_i ? ENCODING : IDLE;
ENCODING: state 《= encoder_clear_start ? CLEAR : ENCODING;
CLEAR: state 《= encoder_end ? IDLE : CLEAR;
default: state 《= IDLE;
endcase
end
end
/*********************************************************************/
// 符号计数器
/*********************************************************************/
always @(posedge clk)
begin
if(!rst_n)
datain_cnt 《= 8’d0;
else
datain_cnt 《= encoder_enable ? (datain_cnt + 1‘b1) : 8’d0;
end
/*********************************************************************/
// 移位寄存器更新
/*********************************************************************/
always @(posedge clk)
begin
if(!rst_n)
shift_reg 《= 6‘d0;
else
shift_reg 《= encoder_enable ? {shift_reg[4:0], uncoded_bits} : 6’d0;
end
/*********************************************************************/
// 编码结果输出
/*********************************************************************/
always @(posedge clk)
begin
if(!rst_n)
coded_bits 《= 2‘d0;
else begin
case(state)
IDLE:
coded_bits 《= 2’d0;
CODING:
begin
coded_bits[0] 《= shift_reg[5] ^ shift_reg[4] ^ shift_reg[2] ^ shift_reg[1] ^ uncoded_bits;
coded_bits[1] 《= shift_reg[5] ^ shift_reg[2] ^ shift_reg[1] ^ shift_reg[0] ^uncoded_bits;
end
CLEAR:
begin
coded_bits[0] 《= shift_reg[5] ^ shift_reg[4] ^ shift_reg[2] ^ shift_reg[1];
coded_bits[1] 《= shift_reg[5] ^ shift_reg[2] ^ shift_reg[1] ^ shift_reg[0];
end
default:
coded_bits 《= 2‘d0;
endcase
end
end
/*********************************************************************/
// 启动信号输出
/*********************************************************************/
always @(posedge clk_fpga)
begin
if(!rst_n)
e_start_o 《= 1’b0;
else begin
e_start_o 《= e_start_i;
end
end
结语
关于卷积码编码及译码实验的相关介绍就到这了,如有不足之处欢迎指正。
相关阅读推荐:什么是卷积码
相关阅读推荐:卷积编码是什么
-
卷积码编码及译码算法的基本原理2022-04-28 14665
-
在FPGA上实现咬尾卷积码的最优算法设计2019-05-03 6418
-
卷积码编码和维特比译码的原理、性能与仿真分析2018-11-14 14103
-
基于C语言的卷积编码实现 浅谈卷积和滤波之区别2018-08-21 3719
-
卷积码编码器怎么画 浅谈卷积码编码器设计2018-08-20 15196
-
基于FPGA的卷积码译码器的方案2011-10-12 1962
-
基于OCDMA的新型卷积码译码方案2010-08-26 964
-
卷积码/Viterbi译码,卷积码/Viterbi译码是什么2010-03-18 2451
-
卷积码的Viterbi高速译码方案2010-01-06 752
-
什么是卷积码? 什么是卷积码的约束长度?2008-05-30 20027
全部0条评论

快来发表一下你的评论吧 !

