卷积码编码译码程序仿真程序 卷积码应用详解

本文主要是关于卷积码的相关介绍，简要分析了卷积码编码译码程序仿真程序，希望通过本文能让你对卷积码有更深的认识。

卷积码

卷积码是一种差错控制编码，由P.Elias于1955年发明。因为数据与二进制多项式滑动相关故称卷积码。卷积码在通信系统中应用广泛，如IS-95，TD-SCDMA，WCDMA，IEEE 802.11及卫星等系统中均使用了卷积码。

卷积码使用（n，k，L）表示，码率为R。

n为输出码字；

k为输入的比特信息；

L为约束长度，也称为记忆深度。

R表示为R = k/n。

卷积码是一种有记忆的纠错码，编码规则是将k个信息比特编码形成n个比特，编码后的n个码元不但与当前输入的k个信息有关，仍与之前的L-1组的信息有关。

卷积码译码

卷积码译码是指按最大似然法则译码，对二进制对称信道（BSC)来说，它等效于最小汉明距离译码。在这种译码器中，把接收序列和所有可能发送序列进行比较，选择一个汉明距最小的序列判作发送序列。由于信息序列、编码序列有着一一对应的关系，而这种关系又惟一对应网格图的一条路径，因此译码就是根据接收序列R在网格图上全力搜索编码器在编码时所经过的路径，即寻找与R有最小汉明距离的路径。 [1] 

与分组码不同，卷积码编码后的n个码元不仅与当前段的k个信息有关，还与前面的N-1段信息有关，编码过程中互相关联的码元个数为nN。卷积码的纠错性能随N的增加而增大，而差错率随N的增加而指数下降。在编码器复杂性相同的情况下，卷积码的性能优于分组码。

卷积码编码译码程序仿真程序

卷积码又称连环码，他是非分组(没有固定长度)有记忆编码，但也是一种线性码，码的结构简单，其性能在许多实际情况优于分组码，通常更适用于向前纠错，是一种较为常见的纠错编码。卷积码其编码器在任一规定时间内产生的n个码元，不仅取决于k个信息位，还取决于前N-1段规定时间内的信息位。整个编码过程可以看成是输入信息序列与由移位寄存器和模2加法器的连接方式所决定的另一个序列的卷积，卷积码由此得名。这N段时间内产生的码元数目nN称为卷积码的约束长度。通常将卷积码记作（n,k,N）,其中k为一次移入编码器的比特数，n为对应于k比特输入的编码输出。其编码效率为R=k/n。

卷积码结构是“信息码、监督位、信息码、监督位…(m1,c1,m2,c2,m3,c3...)”。

c1=0+m1

c2=m1+m2

c3=m2+m3

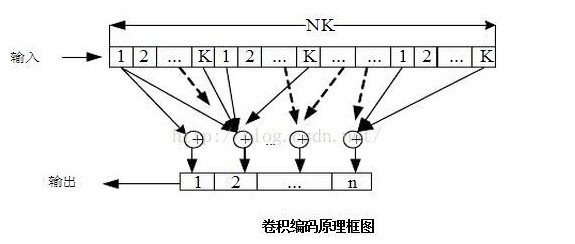
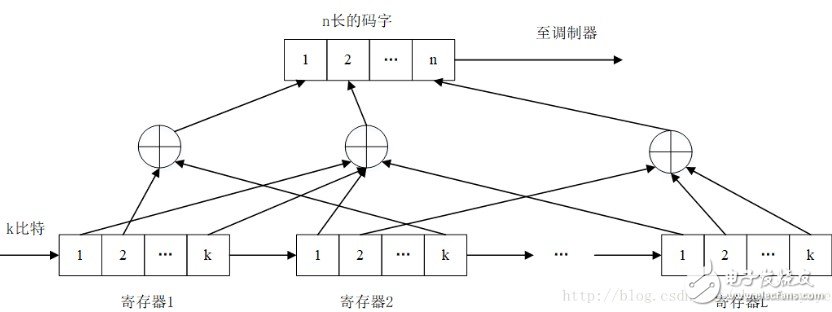
卷积码编码器

（1） 有k个输入信息端，n个输出端（k

（2） 通常称K为约束长度（一般来说，约束长度越大，则码字纠错 性能越好）。  

（3） 码的效率：k/n  

（4） 编码前，k(K-1)个寄存器单元全部复位清零。    

（5） 由于一段消息不仅影响当前段的编码输出，还影响其后m段的 编码输出，所以称参量K=m+1为卷积吗的约束比特长度为 K*n·==。   

(6)注意进入卷积编码器的最后m段消息仍是要编码输出的消息，对这最后m段消息的编码处理，称作卷积编码的结尾处理。一种常见的结尾处理方法是额外输入m段无效的0数据比特，一方面将存储的m段消息编码全部推出，另一方面保证编码器回到全0的初态。 

function [out_put,out_G,out_k0] = convolution(baseband_out)

　　G = ［1，0，1，1;1，1，1，1］; % Generation Matrix G of CC（卷积编码器）

　　k0 = 1; % Number of bits was input into CC

　　input = baseband_out; % input data

　　%查看是否需要补0，输入input必须是k0的整数倍

　　if rem（length（input），k0） 》 0 % whether add 0

　　input=［input，zeros（size（1:k0 - rem（length（input），k0）））］;

　　end

　　n=length（input） / k0; %% 把输入比特按k0分组，n为所得的组数。

　　%检查生成矩阵G的维数是否和k0一致

　　if rem（size（G，1），k0） 》 0 % check the row of G whether identical to k0 %size（A， dim）dim=1表示取矩阵的行数，dim=2表示取矩阵A的列数。

　　error（‘Error，G is not of the right size.’）

　　end

　　%得到约束长度K和输出比特数n0

　　K=size（G，2） / k0; % restrict length

　　n0=size（G，1）; % ouput length

　　%在信息前后加0，使存贮器归0，加0个数为（K-1）*k0个

　　u=［zeros（size（1：（K - 1） * k0）），input，zeros（size（1：（K - 1） * k0））］; % add 0 2（K-1）*k0个以保证编码器是从全0开始，并回到全0状态。

　　u1=u（K * k0：-1:1）; % UU matrix

　　%将加0后的输入序列按每组K*k0个分组，分组是按k0比特增加

　　%从1到K*k0比特为第一组，从1+k0到K*k0+k0为第二组，。。。。，

　　%并将分组按倒序排列。

　　for i=1:n + K - 2 % Grouping 加零以后总共组数

　　u1=［u1，u（（i + K） * k0：-1:i * k0 + 1）］; % Grouping

　　end

　　uu=reshape（u1，K * k0，n + K - 1）; % generate uu， a matrix whose columns are the contents of %生成一列是一组共n+K-1（列）组

　　% conv. encoder at various clock cycles.

　　out_put = reshape（rem（G * uu，2），1，n0 * （K + n - 1））; % % determine the output %rem（G * uu，2）相当与对矩阵的摩尔运算转化成二进制数%

　　out_G = G;

　　out_k0 = k0;

　　% % write the output to the encodetext

　　% result = fopen（encodetext， ‘w’）;

　　% for i = 1:n0*（L+n -1）

　　% fwrite（result， output（i）， ‘bit1’）;

　　% end

　　% fclose（result）

　　MATLAB实现

　　function coded_bits = tx_conv_encoder（in_bits， ConvCodeGenPoly）

　　% 卷积编码

　　% in_bits： 输入未经编码的信息比特

　　% ConvCodeGenPoly： 卷积编码的生成多项式

　　% coded_bits： 编码后的比特

　　number_rows = size（ConvCodeGenPoly， 1）; % 编码输出的路数n

　　number_bits = size（ConvCodeGenPoly， 2） + length（in_bits） - 1; %编码输出单路的比特数

　　coded_bits = zeros（number_rows， number_bits）;

　　for row = 1:number_rows

　　coded_bits（row， ：） = rem（conv（in_bits， ConvCodeGenPoly（row， ：））， 2）;

　　end

　　%多路输出并成一路（并转串）

　　coded_bits = coded_bits（：）;

　　这里将卷积编码封装成了一个函数，可以在调用时才确定生成多项式，对于上面给的情况，matlab调用代码如下：

　　ConvCodeGenPoly = ［1 0 1 1 0 1 1;1 1 1 1 0 0 1］; % 生成多项式：133和171

　　uncoded_bits = ［1 0 1 0］;

　　coded_bits = tx_conv_encoder（uncoded_bits， ConvCodeGenPoly）;

　　结语

　　关于卷积码编码译码程序仿真程序的介绍就到这了，如有不足之处欢迎指正。

相关阅读推荐：什么是卷积码

相关阅读推荐：浅谈卷积编码在通信中的应用