博士真情分享：电磁场仿真与片上电感的优化

大家好，我是贾海昆，非常高兴有这样的机会来跟大家分享一些电磁场仿真的相关经验。我先简单的介绍一下自己。我2009年本科毕业，2015年博士毕业，跟着王志华老师做毫米波集成电路设计的课题。我平常会写一些电路设计的技术文章，发在我个人的公众号和知乎专栏上面，有兴趣的朋友可以去关注一下。这次的讲稿整理后应该也会发上去。

今天我主要想跟大家分享电磁场仿真和毫米波芯片设计的实际经验，都是我平常做设计的一些思考和总结，希望对大家有所启发。

这张图是我博士和博后期间设计的芯片，大部分都是毫米波电路，有模块有系统。四五年的时间，过程中有个很深刻的感觉：那就是随着电路做的越来越多，我对毫米波电路设计的理解也在一直加深。

举两个例子。一是第一版芯片我们几乎只用传输线，为什么呢？因为传输线简单，仿真不容易出错，设计迭代也简单。但实际设计就受到了很大的限制。后来有了一些经验，开始用电感了。再后来，开始大量使用变压器。第二个例子是变压器。最早用变压器的时候，变压器对我就是一个黑盒子，大概仿一个变压器出来，在外面再额外加传输线去做匹配。这样也不是不行。但是不够好。后来才开始理解变压器内部特性，它是有电感量有耦合的。再后来，就发现光考虑电感和耦合还不行，还得把寄生电容加进去。今天再来看片上变压器的话，它有多个参数，每个参数有自己的作用，每个参数都应该被优化。在设计时，我要先知道自己需要什么样的变压器，然后电磁场工具是一个辅助手段，帮我找到我想要的变压器。

这是这次分享的主要内容，电磁场仿真流程，S参数的理解和处理，片上电感的优化，以及最后的总结。

近几年发现电磁场仿真用的越来越广泛了，绝对不仅仅使用在毫米波频段，在射频频段也大量用到了电磁场工具。比如说2017年ISSCC的功率放大器，8篇论文里至少有6篇需要用到电磁场仿真工具。这是其中的两个电路，可以看到用到了大量的变压器和传输线，据我所知，代工厂是没有提供变压器的模型的。如果你不会使用电磁场仿真，那变压器就没法使用了。所以说，电磁场仿真是射频毫米波芯片设计者的必备技能包，否则会处处受限。

选择合适的电磁场仿真工具主要可以从这几个方面来考虑。

第一个，我们要仿的无源结构的频率和尺寸。如果片上元件的话，HFSS、EMX、ADS、Sonnet、Helic都是不错的选择。而封装和PCB，你可能要选择SIWave、ADS、Q3D等等。我曾经对比我SIwave和HFSS 3D Layout仿真同样一个高速封装，得到差不多的结果，一个用了20分钟，一个快9个小时。

第二个是灵活性，功能是否能否满足需求。

第三个，易用性，对EDA平台的支持。还有对工艺的支持。以前我们用65nm的工艺，都是根据文档自己写的tech文件。现在的先进工艺估计不行了，一是代工厂很多关键信息加密了，二是他有一些layout dependent的参数。比如你花了一条1um的线，最后做出来可能不是1um，代工厂会做一些调整。现在一般是你买了哪家的电磁场软件，他已经跟代工厂联系，把tech文件写好了，这些都考虑在内。

第四个是软件使用的仿真原理。原理部分就不细讲了，有兴趣的可以去看看我公众号的一篇文章。仿真器背后采用了什么假设很关键，像EMX和Helic，他们只能仿真层状结构，而且假设衬底地面时无限大的理想地平面，这个一般没有问题，但假如你的衬底非常薄，仿出来有可能就不对了。

现在很多芯片都是倒封装，这样芯片上方也会有一层金属。那用EMX和HELIC仿真的话，这个是没有考虑在内的。我用HFSS建立模型试过一次，假如距离低于50um的话，对电感量会有10%左右的影响。我问过我们用的软件的技术支持这个问题，他说有些客户的确会验证一下封装的影响，这需要手动改tech文件，在芯片上面再加一层金属层，实际操作起来会比较麻烦。

主流的电磁场仿真工具其实很多。这里面估计比较流行的是前三个。HFSS功能最灵活和强大，理论上什么结构都能仿，但是对EDA平台支持的一般。学校里面用的比较多。EMX/HELIC是专门为IC设计优化的，易用性比较好。

好，现在我们来说一下电磁场仿真的流程，这里主要以HFSS为例。EMX的流程更加简单，很多地方软件已经替设计者考虑了。

几乎任何一款电磁场仿真软件的求解流程都是这三步。第一是前处理，包括建立结构、定义材料、设置端口和边界条件等。第二是把材料划分成细小的网格、然后求解电磁场的微分方程或者积分方程，求解各处的场强。但我们电路设计者是没法直接把场强用在电路设计之中的，所以还需要进行后处理。后处理包括导出S参数、计算电磁场分布、辐射等等。

现在来看看如何建立结构。首先是边界条件，我们只能仿真一个有限空间的内容，所以一般会给空气盒子设置辐射边界，给衬底底面设置理想导体边界。第二是对介质层进行等效，可以合理减少计算资源的消耗。这里特别要注意电容，因为做介质层等效的时候很容易改变电容值。右边上图是原始的介质层，下图是等效过后的，可以看到，MIM电容中间所在的层我是没有做等效的。对于通孔我们一般会合并，这一步在版图里完成。但要注意，通孔中是没有横向电流的，如果你等效后通孔中走横向电流，那结果会有一点差异。最后是地平面，为了满足DRC规则，我们会在地平面上挖空，这些孔会导致仿真比较慢，所以可以等效为整个平板，把电导率适当的降低。

在EMX里这些软件都已经帮忙做好了，所以不需要考虑。

现在来看端口设置。这一步尤其重要，电磁场仿真的结果是否合理，很大程度上取决于端口设置是否合理。在HFSS里面有两种端口，集中端口和波端口。但我们几乎只用集中端口。集中端口提供了什么样的激励呢？从这个图可以看出，他就是一个从上边沿到下边缘整个面上均匀分布的电场。我们在设置任何一个端口的时候，都需要想想现实中的场强是否会真的这样分布。所以这一条就很好理解了。假如有很长一个端口，仿真器会假设整个端口电场都是均匀的，但实际上他会呈现一定的分布，这样与实际不符，计算结果就不对了。EMX和ADS同样有这个问题，假如要在长边上加激励，他们都建议在长边上引出一条短边，把激励加在短边上。

我曾经用HFSS仿过一个电感，结果出来非常奇怪，后来一检查，发现集中端口面与金属重叠了，这样他强制认为金属横截面内也有均匀的场，那仿出来结果肯定不对了。

最后一条又是HFSS需要考虑EMX不需要过多考虑的，那就是HFSS中必须给集中端口提供一个回流通路。所以我们仿电感一般都会在外面加一圈地平面。

网格划分和求解到没有太多可以注意的。第一、所有金属选择solve inside，否则Q值不准。它默认是不选的。第二，选Driven terminal的求解方式。第三、solution frequency，即划分网格的频率，倾向于把这个频率设高一点，这样网格划分的细致，结果比较准。这样仿完就可以导出S参数了。

这里总结一下HFSS电感仿真的Check list，可以每次设置完都养成习惯检查一遍。模型尺寸合适、辐射边界和理想导体边界、所有金属都有solve inside、端口有回流途径、选择低阶的basis函数。这里画出了常见的电感仿真端口的加法。

这个图里是我之前仿过的一些无源器件结构图。衬底跟空气盒子都是透明的，所以看不到。那圈蓝色的金属是地平面，用来提供回流路径的。这三个频率逐渐升高。有一个有意思的规律是，频率越低，结构可以做的越复杂。

假如我们现在得到了S参数，那是不是就可以把S参数用在仿真里面了。怎么用呢？一种方法就是把S参数当成一个黑盒子。我最早就是这样做的。我需要一个单转差的Balun，所以我大致仿了一个变压器，然后发现输入不匹配，额外再加三段传输线做输入匹配。这样也不是不能设计。但存在什么问题？第一、额外的匹配消耗额外的面积，加大损耗。第二、这样不了解S参数内部的结构，信心会差一点。第三、你这没法做理论分析，没法写论文。第四、把S参数当作黑盒子放弃了很多的可能性，本来变压器是可以做宽带匹配的，你这样黑盒子就没法优化了。你有一个好的想法，但很有可能，这里不够优化、那里不够优化，最后你的想法带来的好性能完全被这些地方给抵消了。

所以我们说，拿到一个S参数后，并不是你就直接把他丢进仿真器里了，还需要理解S参数。

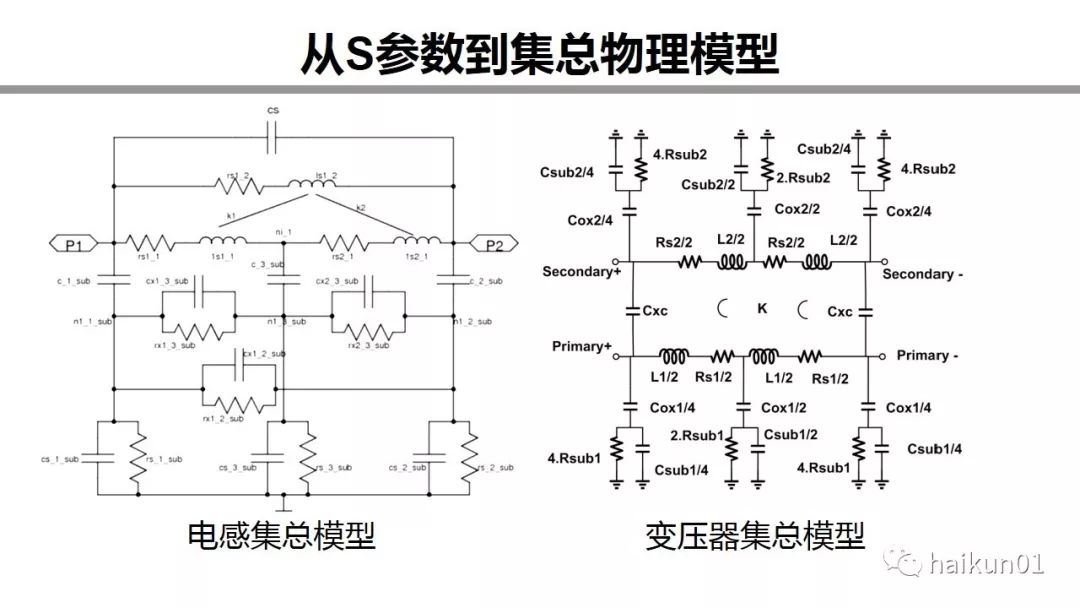
怎么理解呢？第一个方法就是把它转化为集总模型。这里给出了电感集总模型和变压器集总模型的例子。

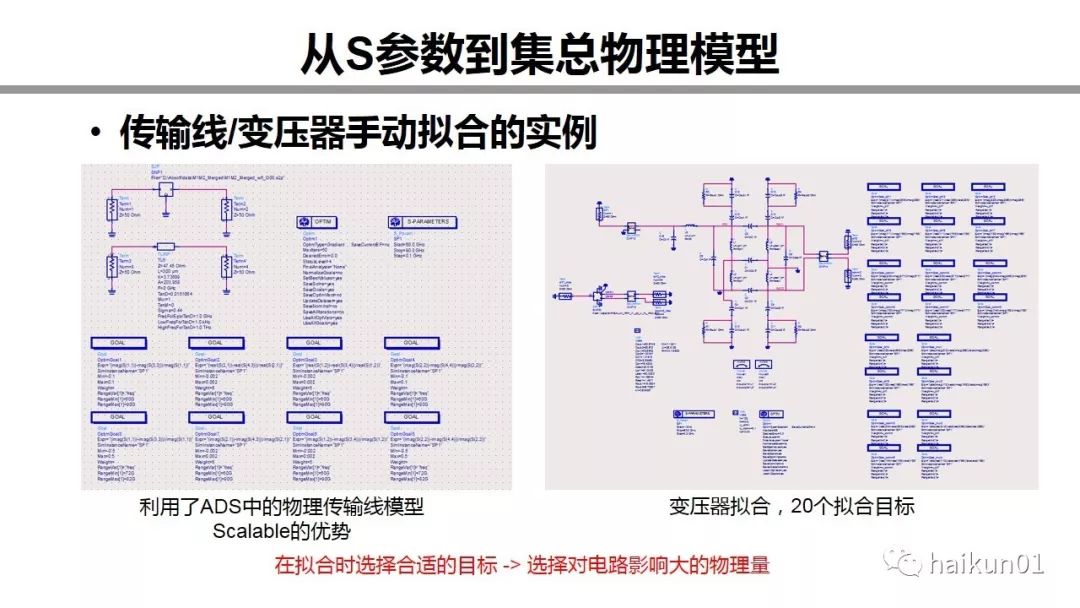
对于HFSS的用户，这步转换只好自己来完成啦。这是两个拟合的例子，原理很简单，你同时仿S参数和你的模型，设置一些目标，让仿真器优化参数来达到目标。对与传输线的仿真，可以使用ADS中的物理传输线模型，很好用。拟合完还可以自由改变传输线的长度，相当于一个scalable的模型。右图是变压器的拟合，这里我用了20个目标。

拟合目标的选择需要进行一些考虑。比如说两端口S参数，实部虚部一共8个参数，你可以用S参数拟合，也可以用Y参数拟合。但我觉得应该选择对电路影响大的物理量来拟合。举个例子，我们要拟合输入匹配，我可以用幅度来拟合，也可以取dB后来拟合。但幅度明显比较好，-30dB和-40dB的return loss对电路没影响，但从数值上来看有30%的差别。取dB的操作相当于放大了小信号部分的权重。

EMX提供一些预设的模型拟合。但也有很大局限性。如果两三个器件在一起，他就拟合不了了。

用S参数仿真和用物理集总模型仿真各有优势。集中模型仿真稳定性好、速度快。无源性能得到保证。没有漏电的问题。但用物理集总模型仿真有一个需要很注意的地方。我们在拟合的时候，实际上损失了一些高阶的效应，比如两个电感之间的微弱耦合。一般没问题，但有些场合这还影响挺严重的。比如说两个不同频率的时钟，时钟信号可能通过无源器件耦合造成串扰，直接转换成Jitter，这样对隔离要求很高，微弱的耦合也有影响。如果用集中模型的话，很难把这么微弱的耦合拟合出来。

所以最终大家会采用S参数仿一个整体的，把各种效应都包含进来。但S参数仿真经常遇到一些头疼的问题。有一些推荐的设置和解决方法。这里先不讲了。

好，现在我们得到了集总模型，但是对于理解依然过于复杂了。前面的变压器有30个参数，我在理论计算时不可能都考虑进去的。那我们怎么更直观的理解模型的S参数？

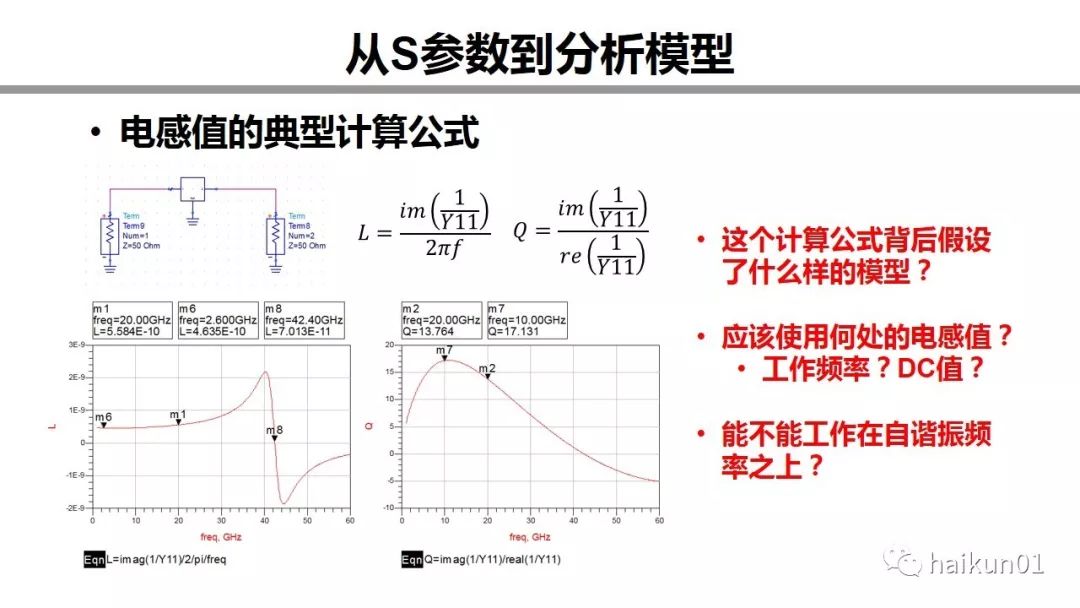
我这里以电感为例。假如我们拿到一个电感的S参数，我们知道可以采用这两个公式去计算电感值和Q值。得到的典型曲线长这个样子。那现在问题来了。这个计算公式背后假设了什么样的模型？这个电感感值是随频率变化的，那我们应该使用什么频率的感值？工作频率还是DC频率？那这个电感可不可以工作在自谐振频率之上？

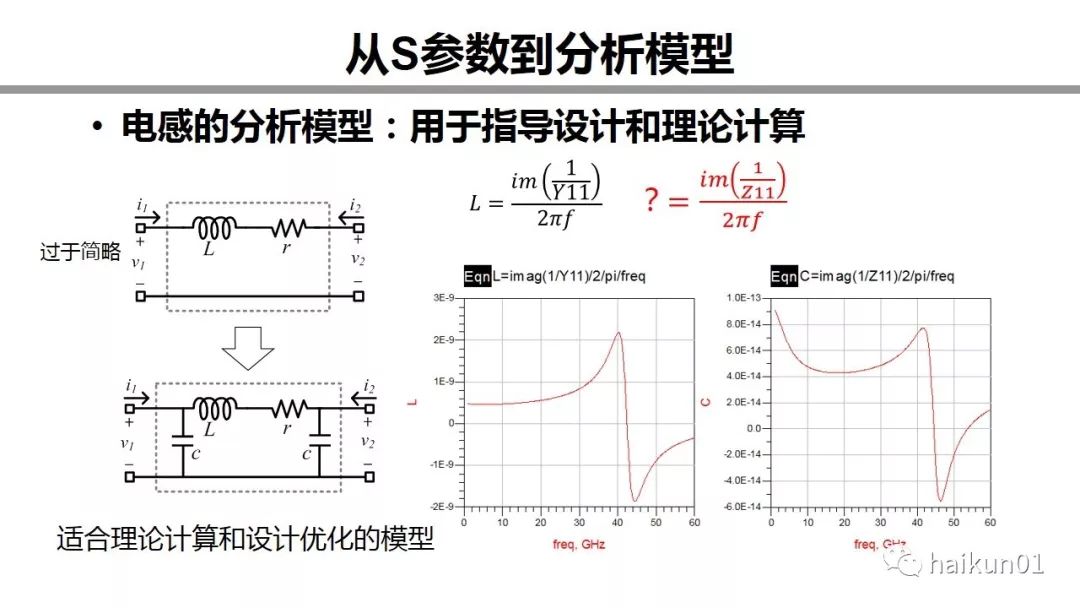
第一个问题的答案在这里。我觉得L这个公式背后实际上是假设了电感和电阻串联的模型。Y参数，2端口短路，虚部是感性，实部是阻性。但实际上这个公式过于简略了，完全忽略了电容。只有在频率远低于自谐振频率时才成立。一个最适合理论计算和设计分析的模型是下面这个。所以你看虚部，实际看到的是电感和电容共同的作用。如果我们用Z参数，会算出什么呢？Z参数，2端口开路。当频率远低于谐振频率时，电感忽略，Z参数基本上计算的就是电感的对地寄生电容。

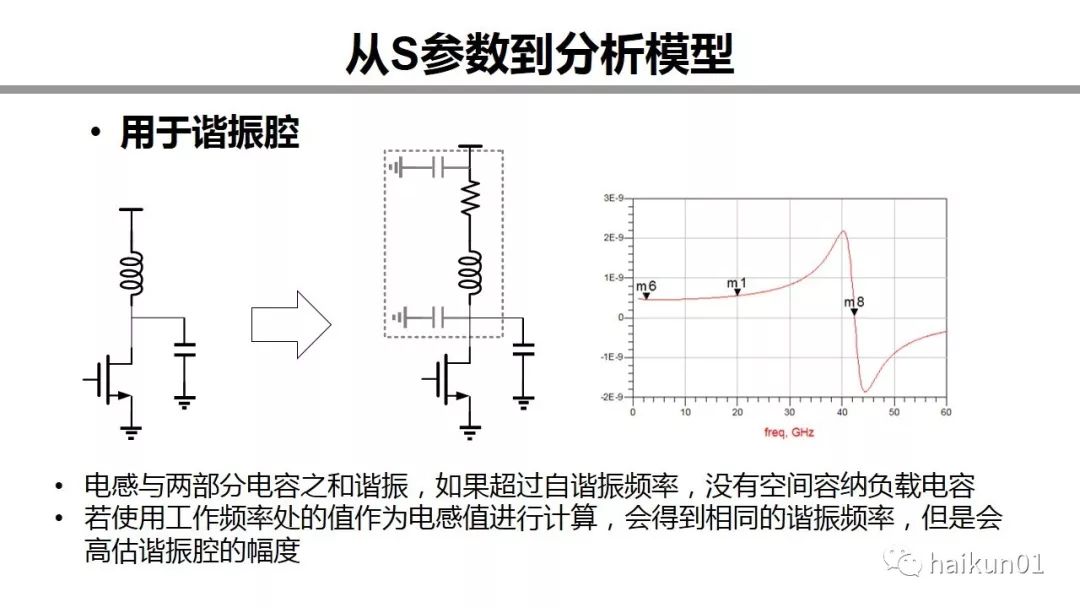
下面我们再来回到后面两个问题。假如我们把电感用于谐振腔。电感实际上是与两部分电容之和来进行谐振，一部分是电感本身的寄生，另一部分才是负载电容。所以，在这种情况下，如果工作频率高于自谐振频率，说明电感在这个频率已经没有吸收电容的空间了。假如你需要容纳的负载电容小一点，那自谐振频率就可以跟工作频率接近一点。假如使用工作频率的电感值进行理论计算，得到的谐振频率应该是相同的。但是，你会高估谐振腔的幅度。谐振腔的幅度等于2pifL。这条曲线工作频率出的值不都是感值，相当于你把一部分容性当成了感性，所以会高估幅度。

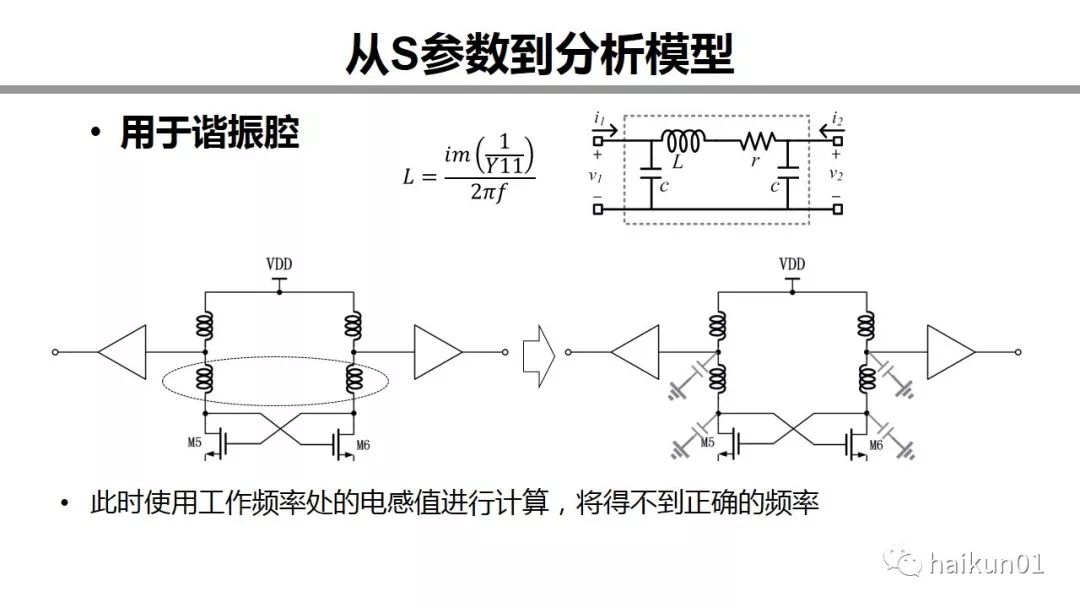
这又是我以前遇到过的一个例子。我要仿这样一个LCLC的网络。我先用理想元件仿真，得到我需要的电感量，然后仿了一个电感，用这个公式算的电感量跟我所需的电感量一样。但一代近电路，发现频率降了好多。为什么呢？在用这个公式计算Y参数时，二端口是短路的，所以那一边的电容被忽略掉了。但在LCLC网络里，这一部分电容对电路也有影响。

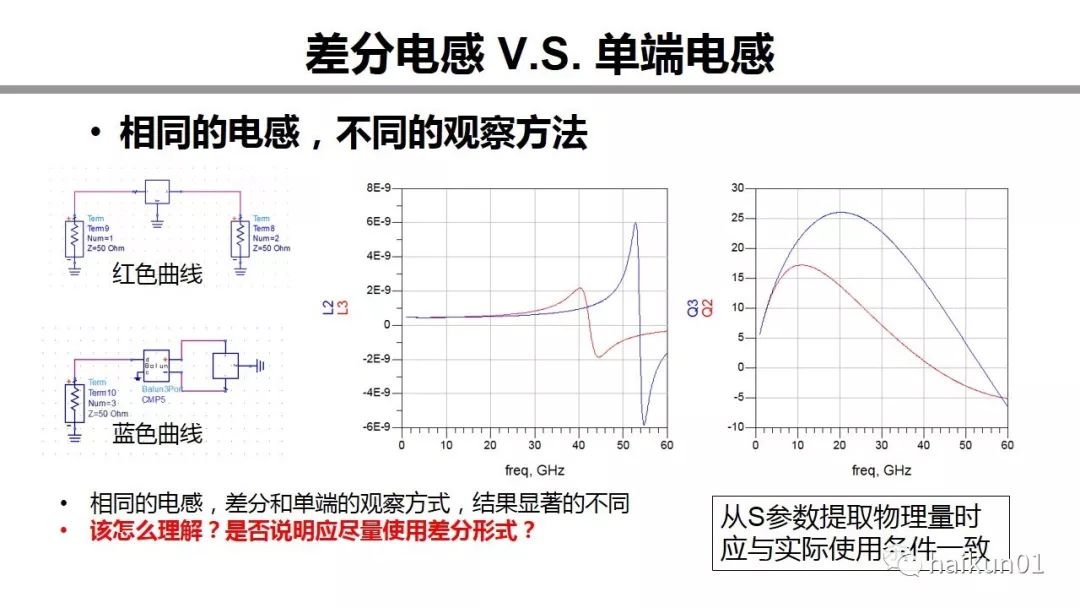
再有一个就是，相同的电感，用差分和单端的方式观察，结构会显著的不同。DC电感值差不多，但差分的自谐振频率高很多，Q值也要高很多。这是为什么呢？是否说明应尽可能使用差分形式的电感？我们后面会继续提到。有一点启示时，你在从S参数中提取物理量时应该与实际的使用条件一致。

这里总结一下从S参数到分析模型。分析模型是我自己起的一个名字，跟物理模型区分。我自己在用电感做设计的时候，一般采用这样的过程，第一步先拿带电容的分析模型对电路进行仿真和优化。确定我需要的电感值Q值和能容忍的C。因为你可以自己随便设这些值，不需要用HFSS迭代，所以这一步仿真速度会比较快。第二步才是用电磁场仿真仿电感，通过S参数提取出LC和Q。总之一句话，我们要先知道需要什么样的电感，电磁场仿真工具只是找到它的工具。

接下来，我会把这些理解应用到电感的版图优化里。这也是我最近遇到的一个例子。我觉得整个逻辑挺有趣的，而且很有启发性，所以跟大家分享一下。

在看具体例子之前先说一些宏观的。电感优化的关键因素有哪些？我觉得有下面四个方面。第一步是理解电路，我们到底要求电感的哪个参数？比如说用于扩展带宽的电感Q值就不重要，反正最后还要串一个电阻，C比较重要。而在VCO和谐振腔里，Q值就非常重要了。只要先知道了哪个重要才知道怎么优化是吧。第二部是理解寄生的来源，寄生主要是由谁贡献。第三步是要理解工艺的金属选项，比如每层金属有多厚啊，层与层的间距啊，是侧边寄生比较大还是对地寄生比较大。第四步很有趣，电感本身是个集中元件，但你在优化的时候，需要把它当成分布式来处理。后面的例子可以很清楚的看到这一点。

好，现在来看具体的例子。这是某个工艺下一个很普通的对称式差分电感，用顶层金属绕线，一共七圈。2.1nH/19.1G的自谐振频率，5.5的Q值。简单的想想，这个电感有什么问题呢？第一、他绕了七圈，所以最外圈和最内圈的耦合很弱，因此单位长度走线的电感值比较小，所以损耗增加。第二、顶层金属一般比较厚，这里排的很密实，走线侧边电容大，所以降低了自谐振频率。怎么解决呢？一个简单的方法，把线间距拉大。但这样的副作用是，外圈和内圈耦合更弱了，电感密度小，走线变长，损耗又变大。那还没有其他方法？

好，这里我做了第一步的改进。充分利用工艺提供的金属层。现在电感用顶层和次顶层走线。他们的厚度是相同的。大家想像一下立体画面。第二四六圈在立体图上是凹陷下去的，是吧，所以，走线的边缘电容减小了，很直接的好处就是谐振频率从19.1G提高到了26.8G，峰值Q也从5.5提高到了6.8。面积没变、电感密度没变。像是白得来的好处。

这一页我有进行了第二步的优化。还是两层金属，相同的面积、相同的电感量。但自谐振频率从26.8进一步提高到了31.5，Q值从6.8提高到了7.6。没有代价，性能全方位提高。这里其实是优化了走线的方式。这个图没看清也先别急。下一页有更清楚的解释。

这一页我把两个电感画到了一起。先看左边的这个。如果我们把半圈线圈当成一个小电感，那么从正端出发最外面的这半圈电感，它往里紧贴着的半圈电感是属于负端的。所以他们之间的寄生电容实际上是跨接在正端和负端之间。那右图中的双重走线呢？通过改变走线方式，从正端出发，第一个半圈电感的内圈半圈电感还是属于正端，所以这个寄生电容的连接位置改变了。大家想想弥勒效应，哪种情况下这个电容对自谐振的影响大？明显是普通走线。极端情况下，左图的这个电容要乘以二，而右图的电容可以忽略掉。所以说性能的提高来源于寄生电容的重新分布。

这里把差分电感画成了分布的形式。从两侧朝中心虚地点，寄生电容的影响越来越小。所以我们在绕电感时，也应该尽量把它往中心推。

这张图我把电感重新花了一下，大家下来可以仔细看看线是怎么走的。能看的更清楚。

下一步优化呢，就是把走线压的更密实，这样外圈内圈之间耦合加强，电感密度变大了。面积从41x41减小到了35x35，但也付出了少量自谐振频率的Q的代价。这实际上已经是个双重走线的差分堆叠电感了。

最后一步，我把上一个电感里的一些弯线给拉直了。最终电感量有所下降，自谐振频率提升到33.9，Q提升到7.8。假如把正方形变成八变形，Q值还能提高0.5左右。

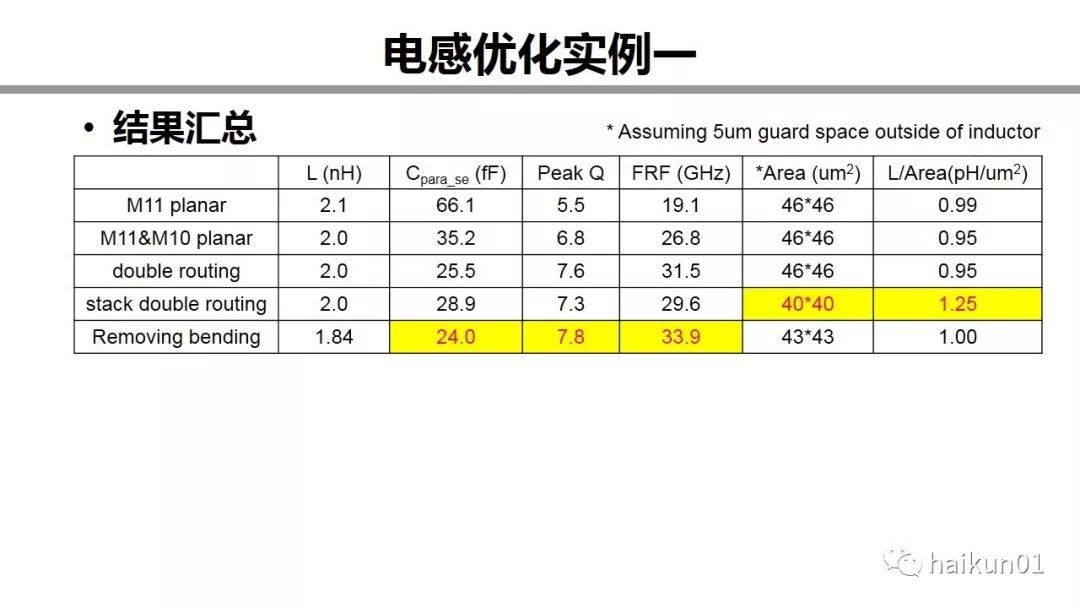
这里做了一些汇总。大家可以看到，我们经过了这些优化后，电感的性能是全方位优于前面没有优化的电感的。不需要折中。付出的代价就是知识。

这里给一个毫米波的例子。毫米波电感一般圈数比较少，所以优化空间小。但依然是有效的。我曾经做的一个设计，就刻意把电感连线的接头做细了。这样可以减小关键部位的寄生电容。中心的部分可以适当的做出，减小电阻。因为不同位置的寄生电阻影响应该是一致的。

好了，我要说点心灵鸡汤了。这个例子实际上能给我们一些启示。第一个，就是选择合适层次的模型的力量。比如说电感的物理模型，够准确，但是太复杂了啊。我没法对着那个来形象化的理解电路。我宁愿损失一点精度，让我更好的分析和理解。繁中取简是工程师必须能做的。第二个启示就是，了解是优化的前提，了解的越深入优化的越好。假如我把电感当成一个黑盒子，不知道内部长什么样子，那肯定没法优化。只有把电感细化成每一小段走线，才能更好的优化。第三个启示是解决问题的方式，不止电感，任何问题都是。要先定位问题在哪儿。自谐振频率低、说明那是寄生电容大，那是寄生电容的主要来源，找到了来源，那好办了，我对症下药，把它推到不重要的地方去。

好了，今天分享的内容大概就到这里。由于时间关系，还有一些点没有讲到。希望以后还有机会更大家交流。希望今天的内容对大家能有一定的启发。