

基于FPGA的DDS设计
今日头条
描述
最近在学习基于FPGA的DDS设计,借此机会把学习过程记录下来,当作自己的学习笔记也希望能够帮助到学习DDS的小伙伴。
DDS(Direct Digital Synthesizer)直接数字合成器,这是直译过来的名字。设计人员一般把它叫做信号发生器,用它来产生一些数字意义上的波形。它的意义还是挺大的,例如我们学习滤波器,就需要一个高低频率叠加的波形,现时生活中到处都是,可以在设计中,怎么能做出这样的波形呢?学习各种载波调制,需要将信息加载到载波上,而载波也一般都是一定频率的正弦波。DDS就是能够产生这种波形,对于学习数字信号处理以及信号调制解调等有很大的作用。
FPGA是数字电路,怎么产生模拟的波形呢?如果单纯的使用FPGA是无论如何也产生不了连续不断的波形,一般都是使用FPGA产生数字信号,再利用DAC(Digital -to- Analog Converter)转化成为模拟的波形(如图1)。DAC芯片是一堆模拟电路的东西了,如果感兴趣的小伙伴可以在自己学习一下数字信号转化为模拟信号的过程。
图1
FPGA是数字信号,通过DAC转化为模拟值,笔者在进行学习的时候一直有个疑问:既然FPGA是数字信号,那么也就只能输出数字信号,输出相邻的两个点中间一定是有一定距离的,输出的模拟波形应该像楼梯一样(有一定的幅值跳跃),而不是连续变化的,像这种情况下还是我们还可以用吗?答案是肯定的,如果“楼梯”的高度跳跃很小,并且在一个周期中有很多小的跳跃,那么就是可以用的。其实微积分的概念和这个道理应该差不多就是用无限多的矩形来近似曲线(如图2)。
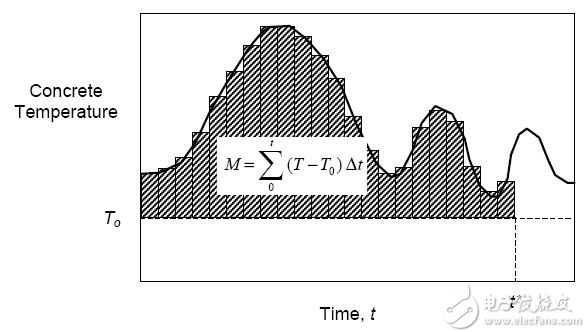
图2
所以在设计时,只要将波形的一个周期(周期波形)中分成N段输出就可以了。
DDS的实现一般都是由频率控制器、相位累加器和波形存储器构成(如图3)。
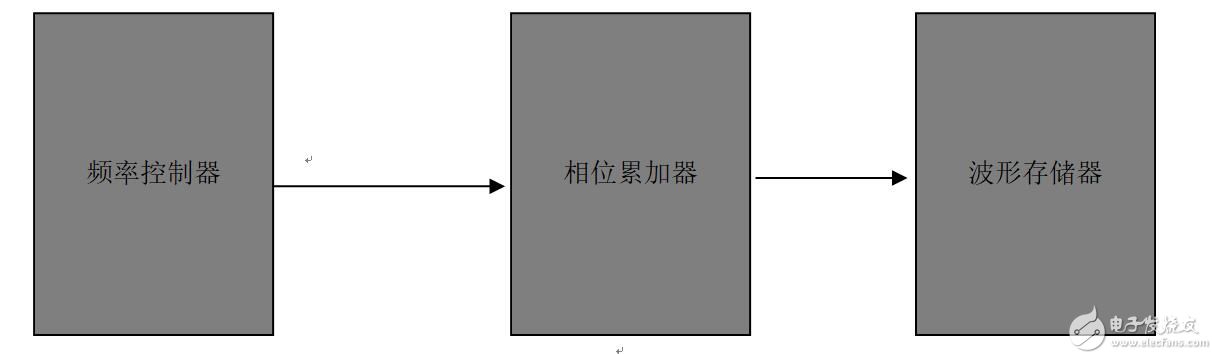
图3
刚刚开始的时候百度到这个信息,笔者也不太理解,经过一段的时间思考,大概明白了其中的设计原理。我们直接从最终的输出开始分析,要输出的一个波形(数字意义上),例如正弦波。那么怎么输出呢,可以给出一个公式sin(2*pi*n/256),将n从0增长到255,就可以输出一个波形。如果这么写的话,就已经把一个周期分成了256份,也可以分成任意份,为了方便数字电路设计,一般都是2的整数次幂份。以下分析都当作一个周期分为256份。n等于一个数值就会输出一个值,把n所对应的位置看作是相位。例如n等于64时,输出的值正好对应于相位pi/2时。在FPGA中去计算sin,一般都是利用查表法,也就是说将一个周期分为N份,当输入的值比较接近与某一个相位时,就把这个相位点的值输出。那其实也就是把波形等分多份,存储在存储器中,而此时存储器就叫做波形存储器。存储器的输出是按照输入地址来决定的,如果想要输出一个完整的不断的波形,就需要地址从最小到最大不变循环,而存储器就会不断的输出波形。地址从最小到最大的累加,就被成为相位累加器。如果相位累加器1S从最小到最大循环了1000次,那么输出的波形的频率就为1KHz。故而相位累加器累加的速度决定输出波形的频率,而累加速度是由外部控制器来决定,所以此控制器被称作频率控制器。
原理就是上述的那样,下面可以考虑如何来实现上述的过程。
在设计中,笔者采用INTEL FPGA来实现,故此采用Quartus Prime 18。首先制作波形存储器,在FPGA中有很多存储器资源可以来用,在此选择ROM来当作存储器。利用ROM当存储需要制作初始化文件.mif或者.hex,这两种都可以,在这里采用.mif文件。
.mif在Quartus 中显示为一个一个小区域(如图4),但是其实就是一种文件格式(如图5)。

图4
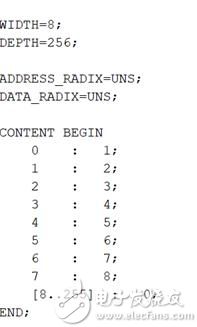
图5
利用某些计算工具将数值计算出来,然后填入表格中,这种速度太慢,也太麻烦。我们一般采用下面所述的两种方法:
利用mifmaker软件生成(QQ群:173560979群文件中),此软件用起来比较简单。只需要简单的设置“设定波形”即可。在设定成功后,点击“文件->保存”即可生成对应的.mif文件(如图6)。
图6
另外一种方法就是利用matlab实现,此方法要求设计者要有一定的matlab基础。源码如下:
clear;
clc;
width = 8;
depth = 256;
file_handle = fopen('sin.mif','w+');
fprintf(file_handle,'--Created by Author xxx\r\n');
fprintf(file_handle,'WIDTH = %d;\r\n',width);
fprintf(file_handle,'DEPTH = %d;\r\n',depth);
fprintf(file_handle,'ADDRESS_RADIX = HEX;\r\n');
fprintf(file_handle,'DATA_RADIX = HEX;\r\n');
fprintf(file_handle,'CONTENT BEGIN\r\n');
for i = 0 : depth-1
fprintf(file_handle,'%4x : %4x ; \r\n',i,floor((0.5+0.5*sin(2*pi*i/depth) ) *(2^width-1)));
end
fprintf(file_handle,'END;\r\n');
fclose(file_handle);
产生了.mif后,就可以加载到ROM中。在quartus工程中,采用50MHz的时钟来进行驱动整个设计,让rom的地址每个时钟周期增加1。经过仿真可以得到正弦波(如图7)。
图7
产生了正弦波,在设置modelsim时,因为波形是按照无符号生成的数据,所以在设置成为模拟之前要先把进制改为无符号类型。即可产生图7波形。经过使用modelsim工具测试,产生的波形的频率为195.313KHz。我们自己也算以下:系统的驱动时钟为50MHz,一个周期为20ns,256个周期输出一个完整的波形。所以波形的周期为256x20ns=5120ns,经过计算频率为195.3125KHz,与上述使用modelsim工具测试结果一直,只是modelsim测试保留了频率的两位小数而已。
相位累加器每次累加1,产生的波形的频率为195.313KHz,那么只要改变每次累加的数字就可以得到其他频率。如果每次增加的是整数比较好办,那如果每次增加的是带有小数呢?又该如何实现呢?
在DDS设计中,如果相位累加器每个时钟周期累加1,就会输出频率为195.313KHz的波形。如果每个时钟周期累加2,就会输出频率为2*195.313KHz的波形·······,如果每两个时钟周期累加1,就会输出195.313/2KHz的波形······,如果按照这样来设计话,不太方便并且输出波形的频率是不连续的,只能输出一些特殊的频率。
首先我们可以一起考虑一个问题,如果我们想要得到一个累加数字0~9,但是想要每次累加的数字有可能是整数也有可能是小数,那么此时整个计算又不让出现小数,应该怎么做呢?我们可以做一个三位数,然后把百位当作我们的输出,然后每次累加的数字自己可以随意调整,也就是相当于之前可以累加小数,小数最小精度为两位小数。000+011=011,123+001=124。如果按照此中方式,让数字一直不断的累加,数字会从最小到最大,不断循环。但是最高位依然是0~9的变化,只不过0~9变化的周期是受到每次累加的值的影响。如果每次累加001,那么百位0~9的循环就需要1000个累加(不要仅仅想0~900,要不断循环),如果每次累加010,那么百位0~9的循环就需要100个累加。
如果考虑明白上述的问题,那么在DDS中,我们做了一个相位累加器,但是累加器只是负责ROM地址的输出也就是8位的。如果按照上述思想我们可以设计一个位宽为32位的计数器,把计数器的高八位当作ROM的地址。让计数器每个时钟周期累加1,地址从0增长到255,也就是8‘b00000000~8’b11111111,需要整个32位从全0到全1,一共需要2的32次幂个时钟周期,而这个也就是输出整个波形用的时间----波形周期。我们可以算出周期:2的32次幂*20ns,频率为0.01164153218Hz。(这个数字太长了,用f0代替)。每次加1,频率为f0,如果每次加2,频率为2倍的f0。那么我们可以任意整数倍的f0,如果f0足够小(此时f0已经足够小),我们认为可以得到任意频率。如果f0的频率不够小,可以通过增加计数器的位宽来实现。
建议读者不要每次加1去仿真,仿真时间太长,并且有可能导致整个仿真器卡主。笔者在此仿真每次累加100K。
module addr_ctrl (
input wire clk_50m,
input wire rst_n,
output wire [7:0] addr
);
reg [31:0] cnt;
assign addr = cnt[31:24];
always @ (posedge clk_50m, negedge rst_n) begin
if (rst_n == 0)
cnt <= 0;
else
cnt <= cnt + 100_000;
end
endmodule
仿真结果如图8。
图8
每次累加100K,仿真测试频率为1.164KHz。每次累加1,得出的频率为0.01164153218Hz。正好扩大了100K倍。现在我们只要知道做每次累加多少,就能够通过算基础这个频率的多少倍就能算出来频率,但是这么算是会有误差,因为上述得到的频率就是一个近似值。我们可以按照公式去计算频率,假如每次增加N,那么输出波形的周期应该是2的32次幂除以N乘以时钟周期(20ns),用1s除以周期就可以得到频率(如图9)。
图9
通过上面的方法,我们可以轻易知道,累加N所对应的频率。但是在实际应用中,往往是想要某一个频率的波形,而不是有了波形算波形的频率是多少。根据外部要求频率,算出来每次累加N的具体数值,这就是频率控制器。其实也是比较简单的,我们把上述公式转换以下就可以了(如图10)。
图10
把图10当中的公式在FPGA实现,输入F得到N就是频率控制器。在计算中会有可能存在一些误差,因为有可能计算的数值为12345.24,但是在累加时,会按照12345来进行累加,.24会被忽略,往往会带来一个误差,但是此误差一般都是可以接受的。
好了DDS的设计到此结束了,但是如果想要真正输出一个模拟的波形还要驱动一个DAC器件,来达到真正的模拟波形的输出。
笔者水平有限,如果设计中,有什么不妥的地方,恳请大佬们指出来。
欢迎加好友探讨QQ:746833924,QQ群:173560979。
- 相关推荐
- FPGA
-
基于FPGA的DDS设计2012-08-11 0
-
基于FPGA 的DDS 调频信号的研究与实现2012-08-17 0
-
基于FPGA的DDS信号发生器2019-03-18 0
-
如何利用FPGA设计DDS信号发生器?2021-04-09 0
-
如何利用FPGA和DDS技术实现正弦信号发生器的设计2021-04-28 0
-
如何采用FPGA+DDS控制AD9911?2021-04-30 0
-
如何利用FPGA设计DDS电路?2021-04-30 0
-
怎么利用FPGA设计基于DDS的信号发生器?2021-05-06 0
-
怎么实现基于FPGA+DDS的正弦信号发生器的设计?2021-05-11 0
-
求一种基于MCU+FPGA的DDS设计方案2022-01-26 0
-
基于FPGA和DDS的信号源设计2010-02-21 1929
-
基于FPGA的DDS励磁恒流源设计2011-07-16 1963
-
基于FPGA的DDS IP核设计方案2012-04-05 1041
-
基于FPGA的DDS信号源研究与设计_南楠2016-05-16 498
-
基于FPGA 的DDS正弦信号发生器的设计和实现2024-03-24 383
全部0条评论

快来发表一下你的评论吧 !

