

将神经网络视作模型的后果是什么?
电子说
描述
编者按:Microsoft Semantic Machines资深研究科学家、UC Berkeley计算机科学博士Jacob Andreas指出,神经网络不应视为模型,因为神经网络的模型和推理过程不可分割。应该将推理过程视为机器学习问题的一等公民。
在大多数介绍人工智能的材料中,模型和推理过程的区分很关键。例如,HMM(隐马尔可夫模型)是一类模型;维特比算法则是用于推理过程的一种算法,前向传播算法是另一种推理算法,粒子滤波又是一种推理算法。
很多人将神经网络描述为一类模型(他们大概也把神经网络视作模型)。我主张这种观点很有误导性,将神经网络看成纠缠不清的模型-推理对(model-inference pairs)会更有用。“模型-推理对”是一个长而拗口的词,看起来现在也没有什么很好的现成的简称,因此我将用模推(monferences)来指代这一概念。我主张我们应该将神经网络视为模推的一个例子。(搭配某种特定的HMM参数的维特比算法的一种实现,同样是模推。)
我将引用一些现有的论文,这些论文自然而然地符合将神经网络视为模推这一视角——看起来这一想法对许多人来说已经是显然的了。但我认为这一想法未曾被命名,也未曾经过系统的处理。我希望其他人会像我一样,觉得下面的内容是有用的(或者至少厘清了一些东西)。
将神经网络视作模型的后果是什么?让我举一个自己的例子来说明:
我第一次看到循环神经网络的时候,我觉得“这是一个有趣的模型,搭配一个糟糕的推理过程”。循环网络看起来像HMM。HMM有离散的隐藏状态,而循环网络有隐藏状态向量。在HMM中进行推理时,我们保持和输出分布相一致的隐藏状态,但在循环网络中进行推理时,我们仅仅保持单个向量——单个假设,加上贪婪推理过程。如果采用某种建模不确定性的方法,不是更好吗?为什么不像卡尔曼滤波一样对待RNN推理?
这完全错了。探索为什么这是错的,正是本文剩下部分的目标。
简单来说,将循环网络的隐藏状态视作单个假设是毫无理由的。毕竟,一个足够大的隐藏向量可以轻而易举地表示前向传播算法中的整张概率表——甚至可以表示粒子滤波的状态。“HMM隐藏状态 = RNN隐藏状态”这一类比不好;“HMM解码器状态 = RNN隐藏状态”这一类比更好。
让我们通过实验来探索这一点。(本节中的完整代码见git.io/fN91L)。
我随机生成了一个HMM,从中取样了一组序列,并应用经典的最小化风险过程。最终得到的“在线标签”精确度为62.8。
针对这一在线标签问题,另一种完全可以接受(但某种程度上更费力)的生成模推的方法是从HMM中抽取更多样本,然后使用(观测, 隐藏)序列作为RNN网络的训练数据(x, y):
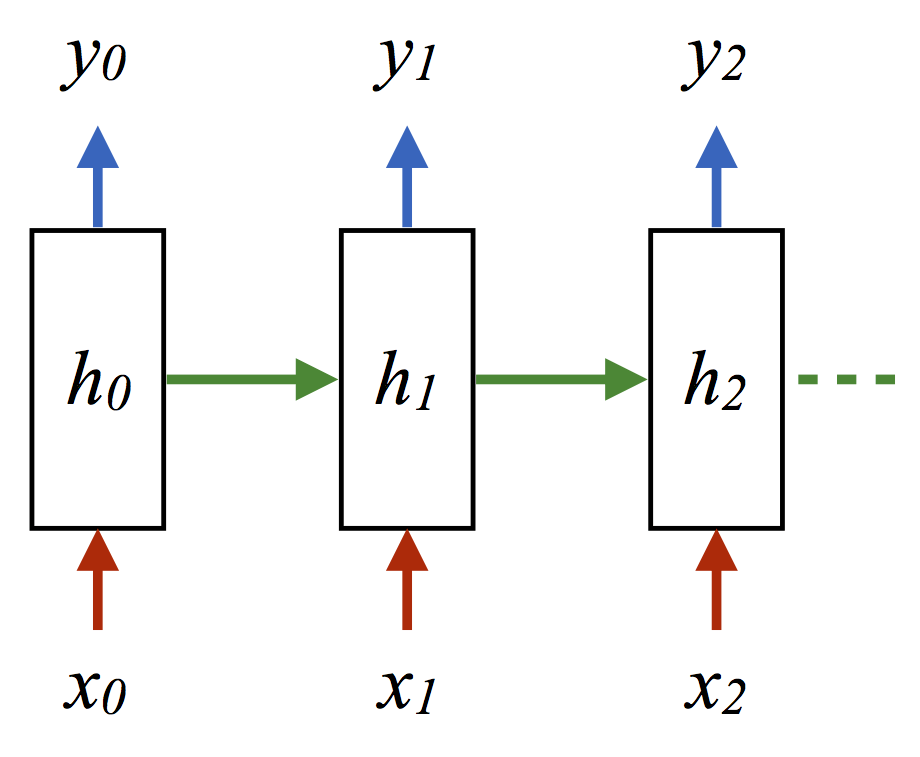
(其中每个箭头表示内积加ReLU激活或log损失)。这一情形下取得的精确度为62.8。
两个精确度是一样的,这仅仅是个巧合?让我们查看一些预测:

所以,甚至当两个模推犯错的时候,都犯了一样的错。
当然,我们知道,就这一问题而言,如果我们应用完整的前向-后向算法,并且同样做出最大化边际概率的预测,能得到稍好的结果。改进的经典过程得到的精确度为63.3。如我们所料,这比上面两种在线模型的表现要好。另一方面,在取自HMM的样本上训练一个双向循环网络同样得到63.3的精确度。
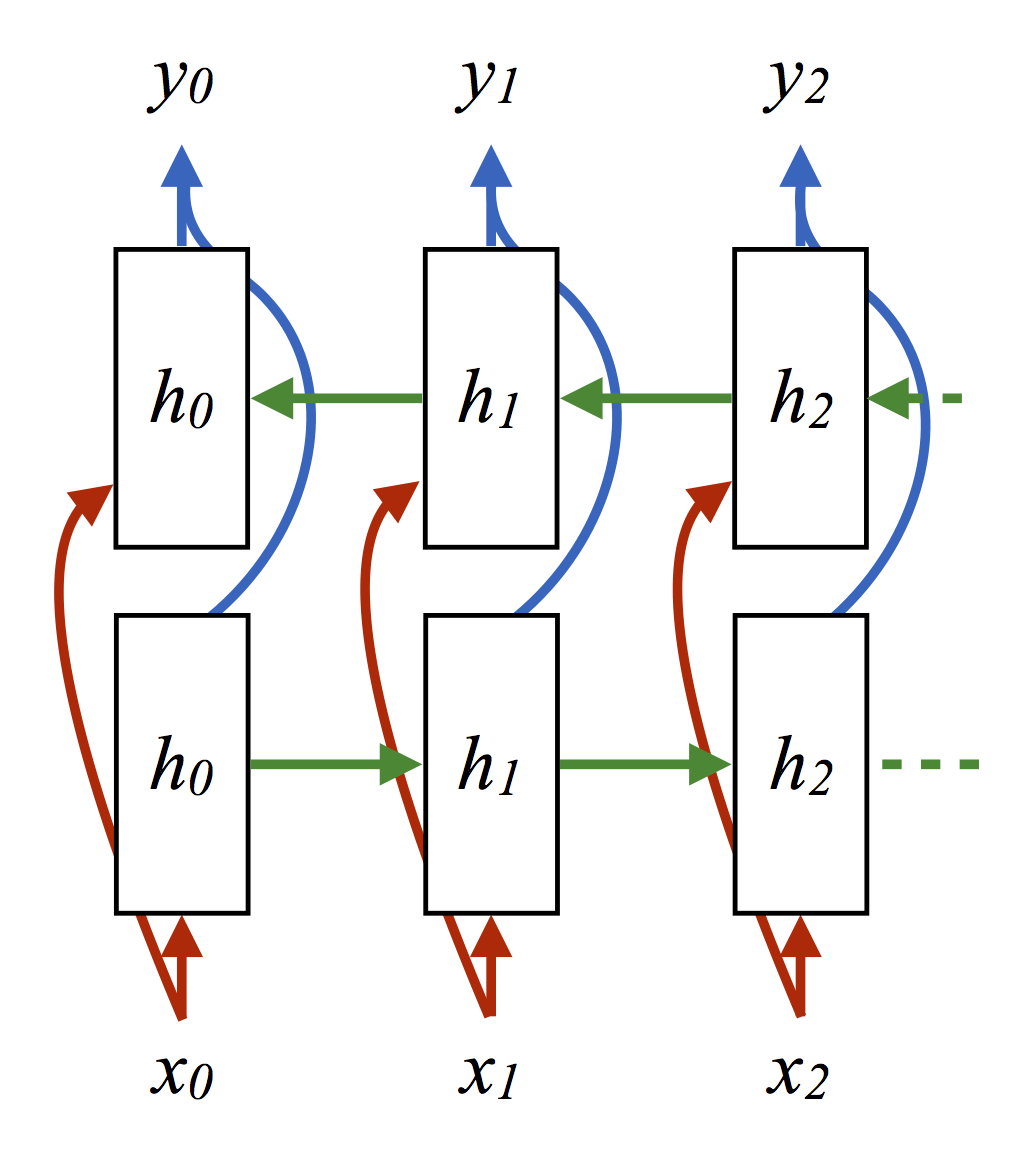
预测取样:
注意,我们这里使用的神经网络没有编码任何关于经典消息传递的规则,并且绝对没有编码任何HMM内部的生成过程。然而在两种情形下,神经网络都成功取得了和结构相同的经典消息传递过程一样好(但没有更好)的精确度。实际上,该神经训练过程相当于一段代码,这段代码和前向-后向算法做出一致的预测,却对前向-后向算法毫无所知!
神经网络不是魔法——当我们的数据实际上是由HMM生成的时候,我们无法指望神经模推击败(信息论上最优的)经典模推。但经验告诉我们,两者的表现一样好。随着我们增强神经架构,以匹配更强大的经典推理过程的算法结构,它们的表现提升了。双向循环网络优于前向循环网络;每个“真”隐藏向量间具有多层的双向网络(arXiv:1602.08210)可能在一些任务上表现更好。
更妙的是,我们也许可以少操心更困难的情形,也就是原本需要手工调整某种逼近推理方案的情形。(例如:假设我们的转移矩阵是一个巨大的排列组合。在经典推理中,重复相乘可能非常昂贵,而尝试取得转移矩阵的低秩逼近则会损失信息。而一个神经模推却具备紧凑地表达模型动力学的潜力。)
目前为止我们讨论的是序列,但在更多结构化数据上同样存在对应。就树形问题而言,我们可以应用某种类似固定树上的内向算法(aclweb/P13-1045),或者整个稀疏化解析表上的内向-外向算法(aclweb/D15-1137)。而对任意图而言,我们可以应用“图卷积”(arXiv:1509.09292),随着图卷积的重复,它开始看起来像是置信传播。
这里有一条一般原则:任何保持离散状态分布的推理算法,都可以转换:
将表单元或离散分布替换为向量
将单元间的信息替换为循环网络
展开“推理”过程(选择一个合适的迭代数)
通过反向传播进行训练
所得的模推至少和相应的经典过程具备同样的表达能力。在有必要逼近的地方,我们可以(至少从经验上说)通过在数据上端到端地训练,学习正确的逼近。
这种通过反向传播逼近推理过程,但并不尝试学习推理函数本身的想法已经提出了有一段时间了。(doi/10.1.1.207.9392、 arXiv:1508.02375)
我认为结合这一框架的各部分至少可以写一篇句法分析的论文,而图结构数据方面还有很多工作可以做。
我说明了模推这一角度是有用的。但是果真如此吗?神经网络确实是模推,而不是模型,这有准确的意义吗?
不。这里有一个基础性的可识别问题——我们无法真正区分“酷炫的模型搭配微不足道的推理”和“神秘的模型搭配复杂的推理”。因此,给定训练好的神经网络,询问它进行推理的模型是哪个同样毫无意义。另一方面,通过蒸馏法训练的神经网络(arXiv:1503.02531)看起来倒挺像“同一模型,不同模推”的良好人选。同时,将神经网络视作模型这一角度也不应该完全忽略:它形成了成果累累的系列工作,将CRF中的对数线性回归模型替换为神经网络(arXiv:1507.03641)。尽管这些方法通常的卖点之一是“你可以保留动态程序”,我们之前论证了这一点在恰当组织的神经网络上同样成立。
不管怎么说,由于机器学习社区这一角落的研究重点在向计划、推理和困难算法问题(nips2015/4G4h)转变,我认为将神经网络视作模推的角度将占统治地位。
除此以外,当我们回顾十年前的“深度学习革命”时,我认为最重要的经验教训是端到端训练解码器的重要性和推理过程,甚至在几乎看起来完全不像是神经网络的系统(arXiv:1601.01705)中也是如此。所以在创建学习系统的时候,不要问:“我的变量的概率关系是什么?”而问:“我如何逼近我的问题的推理函数?”,并尝试直接学习这一逼近。为了高效地达成这一点,我们可以使用我们所知道的关于经典推理过程的一切知识。不过,我们同时也应该开始将推理视作学习问题的一等公民。
感谢Matt Gormley(他的EMNLP演讲让我开始思考这一问题),以及Robert Nishihara和Greg Durrett的反馈。
同样感谢Jason Eisner的金玉良言:“一个拙劣的混成词,因为monference应该是一个像model一样的可数名词,但它的后缀却取自inference这个集合名词。我可没说infedel要好太多……”
-
神经网络教程(李亚非)2012-03-20 0
-
【PYNQ-Z2试用体验】神经网络基础知识2019-03-03 0
-
如何构建神经网络?2021-07-12 0
-
卷积神经网络模型发展及应用2022-08-02 0
-
神经网络模型原理2021-04-21 886
-
卷积神经网络模型有哪些?卷积神经网络包括哪几层内容?2023-08-21 1882
-
卷积神经网络模型原理 卷积神经网络模型结构2023-08-21 979
-
常见的卷积神经网络模型 典型的卷积神经网络模型2023-08-21 2800
-
cnn卷积神经网络模型 卷积神经网络预测模型 生成卷积神经网络模型2023-08-21 1200
-
卷积神经网络模型搭建2023-08-21 928
-
卷积神经网络模型的优缺点2023-08-21 4278
-
构建神经网络模型的常用方法 神经网络模型的常用算法介绍2023-08-28 1012
-
人工神经网络模型的分类有哪些2024-07-05 938
-
人工神经网络模型包含哪些层次2024-07-05 488
-
PyTorch神经网络模型构建过程2024-07-10 439
全部0条评论

快来发表一下你的评论吧 !

