使用TensorFlow框架演示了卷积神经网络在MNIST数据集上的应用

Google产品分析Zlatan Kremonic介绍了卷积神经网络的机制，并使用TensorFlow框架演示了卷积神经网络在MNIST数据集上的应用。

卷积神经网络（CNN）是一种前馈人工神经网络，其神经元连接模拟了动物的视皮层。在图像分类之类的计算机视觉任务中，CNN特别有用；不过，CNN也可以应用于其他机器学习任务，只要该任务中至少一维上的属性的顺序对分类而言是必不可少的。例如，CNN也用于自然语言处理和音频分析。

CNN的主要组成部分是卷积层（convolutional layer）、池化层（pooling layer）、ReLU层（ReLU layer）、全连接层（fully connected layer）。

图片来源：learnopencv.com

卷积层

卷积层从原输入的三维版本开始，一般是包括色彩、宽度、高度三维的图像。接着，图像被分解为过滤器（核）的子集，每个过滤器的感受野均小于图像总体。这些过滤器接着沿着输入量的宽高应用卷积，计算过滤器项和输入的点积，并生成过滤器的二维激活映射。这使得网络学习因为侦测到输入的空间位置上特定种类的特征而激活的过滤器。过滤器沿着整个图像进行“扫描”，这让CNN具有平移不变性，也就是说，CNN可以处理位于图像不同部分的物体。

接着叠加激活函数，这构成卷积层输出的深度。输出量中的每一项因此可以视作查看输入的一小部分的神经元的输出，同一激活映射中的神经元共享参数。

卷积层的一个关键概念是局部连通性，每个神经元仅仅连接到输入量中的一小部分。过滤器的尺寸，也称为感受野，是决定连通程度的关键因素。

其他关键参数是深度、步长、补齐。深度表示创建的特征映射数目。步长控制每个卷积核在图像上移动的步幅。一般将步长设为1，从而导向高度重叠的感受野和较大的输出量。补齐让我们可以控制输出量的空间大小。如果我们用零补齐（zero-padding），它能提供和输入量等高等宽的输出。

图片来源：gabormelli.com

池化层

池化是一种非线性下采样的形式，让我们可以在保留最重要的特征的同时削减卷积输出。最常见的池化方法是最大池化，将输入图像（这里是卷积层的激活映射）分区（无重叠的矩形），然后每区取最大值。

池化的关键优势之一是降低参数数量和网络的计算量，从而缓解过拟合。此外，由于池化去除了特定特征的精确位置的信息，但保留了该特征相对其他特征的位置信息，结果也提供了平移不变性。

最常见的池化大小是2 x 2（步长2），也就是从输入映射中去除75%的激活。

图片来源：Leonardo Araujo dos Santos

ReLU层

修正线性单元（Rectifier Linear Unit）层应用如下激活函数

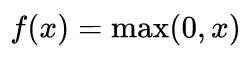
至池化层的输出。它在不影响卷积层的感受野的前提下增加了整个网络的非线性。当然，我们也可以应用其他标准的非线性激活函数，例如tanh和sigmoid。

图片来源：hashrocket.com

全连接层

获取ReLU层的输出，将其扁平化为单一向量，以便调节权重。

图片来源：machinethink.net

使用TensorFlow在MNIST数据集上训练CNN

下面我们将展示如何在MNIST数据集上使用TensorFlow训练CNN，并达到接近99%的精确度。

首先导入需要的库：

import numpy as np

import tensorflow as tf

import matplotlib.pyplot as plt

import pandas as pd

import os

from datetime import datetime

from sklearn.utils import shuffle

编写提供错误率和预测响应矩阵的基本辅助函数：

def y2indicator(y):

N = len(y)

y = y.astype(np.int32)

ind = np.zeros((N, 10))

for i in range(N):

ind[i, y[i]] = 1

return ind

def error_rate(p, t):

return np.mean(p != t)

接下来，我们加载数据，归一化并重整数据，并生成训练集和测试集。

data = pd.read_csv(os.path.join('Data', 'train.csv'))

def get_normalized_data(data):

data = data.as_matrix().astype(np.float32)

np.random.shuffle(data)

X = data[:, 1:]

mu = X.mean(axis=0)

std = X.std(axis=0)

np.place(std, std == 0, 1)

X = (X - mu) / std

Y = data[:, 0]

return X, Y

X, Y = get_normalized_data(data)

X = X.reshape(len(X), 28, 28, 1)

X = X.astype(np.float32)

Xtrain = X[:-1000,]

Ytrain = Y[:-1000]

Xtest  = X[-1000:,]

Ytest  = Y[-1000:]

Ytrain_ind = y2indicator(Ytrain)

Ytest_ind = y2indicator(Ytest)

在我们的卷积函数中，我们取步长为一，并通过设定padding为SAME确保卷积输出的维度和输入的维度相等。下采样系数为二，在输出上应用ReLU激活函数：

def convpool(X, W, b):

conv_out = tf.nn.conv2d(X, W, strides=[1, 1, 1, 1], padding='SAME')

conv_out = tf.nn.bias_add(conv_out, b)

pool_out = tf.nn.max_pool(conv_out, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')

return tf.nn.relu(pool_out)

初始化权重的方式是随机正态分布取样/sqrt(扇入+扇出)。这里的关键是随机权重的方差受限于数据集大小。

def init_filter(shape, poolsz):

w = np.random.randn(*shape) / np.sqrt(np.prod(shape[:-1]) + shape[-1]*np.prod(shape[:-2] / np.prod(poolsz)))

return w.astype(np.float32)

我们定义梯度下降参数，包括迭代数，batch尺寸，隐藏层数量，分类数量，池尺寸。

max_iter = 6

print_period = 10

N = Xtrain.shape[0]

batch_sz = 500

n_batches = N / batch_sz

M = 500

K = 10

poolsz = (2, 2)

初始化过滤器，注意TensorFlow的维度顺序。

W1_shape = (5, 5, 1, 20) # (filter_width, filter_height, num_color_channels, num_feature_maps)

W1_init = init_filter(W1_shape, poolsz)

b1_init = np.zeros(W1_shape[-1], dtype=np.float32) # one bias per output feature map

W2_shape = (5, 5, 20, 50) # (filter_width, filter_height, old_num_feature_maps, num_feature_maps)

W2_init = init_filter(W2_shape, poolsz)

b2_init = np.zeros(W2_shape[-1], dtype=np.float32)

W3_init = np.random.randn(W2_shape[-1]*7*7, M) / np.sqrt(W2_shape[-1]*7*7 + M)

b3_init = np.zeros(M, dtype=np.float32)

W4_init = np.random.randn(M, K) / np.sqrt(M + K)

b4_init = np.zeros(K, dtype=np.float32)

接着，我们定义输入变量和目标变量，以及将在训练过程中更新的变量：

X = tf.placeholder(tf.float32, shape=(batch_sz, 28, 28, 1), name='X')

T = tf.placeholder(tf.float32, shape=(batch_sz, K), name='T')

W1 = tf.Variable(W1_init.astype(np.float32))

b1 = tf.Variable(b1_init.astype(np.float32))

W2 = tf.Variable(W2_init.astype(np.float32))

b2 = tf.Variable(b2_init.astype(np.float32))

W3 = tf.Variable(W3_init.astype(np.float32))

b3 = tf.Variable(b3_init.astype(np.float32))

W4 = tf.Variable(W4_init.astype(np.float32))

b4 = tf.Variable(b4_init.astype(np.float32))

定义前向传播过程，然后使用RMSProp加速梯度下降过程。

Z1 = convpool(X, W1, b1)

Z2 = convpool(Z1, W2, b2)

Z2_shape = Z2.get_shape().as_list()

Z2r = tf.reshape(Z2, [Z2_shape[0], np.prod(Z2_shape[1:])])

Z3 = tf.nn.relu( tf.matmul(Z2r, W3) + b3 )

Yish = tf.matmul(Z3, W4) + b4

cost = tf.reduce_sum(tf.nn.softmax_cross_entropy_with_logits(logits = Yish, labels = T))

train_op = tf.train.RMSPropOptimizer(0.0001, decay=0.99, momentum=0.9).minimize(cost)

# 用于计算错误率

predict_op = tf.argmax(Yish, 1)

我们使用标准的训练过程，不过，当在测试集上做出预测时，由于RAM限制我们需要固定输入尺寸；因此，我们加入的计算总代价和预测的函数稍微有点复杂。

t0 = datetime.now()

LL = []

init = tf.initialize_all_variables()

with tf.Session() as session:

session.run(init)

for i in range(int(max_iter)):

for j in range(int(n_batches)):

Xbatch = Xtrain[j*batch_sz:(j*batch_sz + batch_sz),]

Ybatch = Ytrain_ind[j*batch_sz:(j*batch_sz + batch_sz),]

if len(Xbatch) == batch_sz:

session.run(train_op, feed_dict={X: Xbatch, T: Ybatch})

if j % print_period == 0:

test_cost = 0

prediction = np.zeros(len(Xtest))

for k in range(int(len(Xtest) / batch_sz)):

Xtestbatch = Xtest[k*batch_sz:(k*batch_sz + batch_sz),]

Ytestbatch = Ytest_ind[k*batch_sz:(k*batch_sz + batch_sz),]

test_cost += session.run(cost, feed_dict={X: Xtestbatch, T: Ytestbatch})

prediction[k*batch_sz:(k*batch_sz + batch_sz)] = session.run(

predict_op, feed_dict={X: Xtestbatch})

err = error_rate(prediction, Ytest)

if j == 0:

print("Cost / err at iteration i=%d, j=%d: %.3f / %.3f" % (i, j, test_cost, err))

LL.append(test_cost)

print("Elapsed time:", (datetime.now() - t0))

plt.plot(LL)

plt.show()

输出：

Cost / err at iteration i=0, j=0: 2243.417 / 0.805

Cost / err at iteration i=1, j=0: 116.821 / 0.035

Cost / err at iteration i=2, j=0: 78.144 / 0.029

Cost / err at iteration i=3, j=0: 57.462 / 0.018

Cost / err at iteration i=4, j=0: 52.477 / 0.015

Cost / err at iteration i=5, j=0: 48.527 / 0.018

Elapsed time: 0:09:16.157494

结语

如我们所见，模型在测试集上的表现在98%到99%之间。在这个练习中，我们没有进行任何超参数调整，但这是很自然的下一步。我们也可以增加正则化、动量、dropout。