

运用最优模糊保代价控制对永磁同步电动机混沌系统进行深度实现
描述
摘 要:研究了具有不确定参数非线性系统的稳定最优模糊保代价控制问题。采用T-S模糊模型描述非线性系统,对具有范数有界,时变参数不确定性的非线性系统,得到了存在稳定最优模糊保代价控制器的充分条件,并推算出了相应的线性矩阵不等式(LMI)形式。建立了永磁同步电动机混沌系统的T-S模型,采用最优模糊保代价控制器进行控制,针对不含参数不确定性和含有参数不确定性两种情况进行仿真研究,均得到满意的控制效果。
1 引言
混沌控制是当前混沌运动研究的一个新领域。是实现混沌应用的关键环节。多年来,人们对混沌运动的性质产生了一些广为接受的认识,即混沌轨道的长期趋势是不可预言的,并且混沌运动是难以控制的。1990年E.Ott、C.Grebogi和J.A.Yorke提出控制混沌的思想(OGY控制)产生广泛影响。以后十年,新的研究成果不断涌现。以上方案无须改变系统固有参数,即可实现对混沌系统的有效控制,但是,要求系统参数是定常的。当混沌系统具有不确定参数时,以上方案将失效。近年来,关于不确定参数的混沌系统的控制已引起重视。电力系统中存在着许多混沌现象。其中永磁同步电动机的数学模型是多变量、强耦合的非线性系统,能呈现出非常丰富的动态行为,如极限环和混沌。对其如何进行控制也是一个重要的研究课题。
对于不确定线性系统,基于Riccati方程和线性矩阵不等式(LMI)提出了一系列的鲁棒控制器设计方法。对于不确定非线性系统,现有的研究成果还很少。实践证明,具有线性后件的T-S模糊模型充分利用局部信息和专家经验,能以任意精度逼近实际的控制对象。在考虑模型不确定性的情况下,文献提出了模糊鲁棒控制的概念,并取得了一定的成果。本文针对一类由T-S模糊模型表示的不确定连续非线性系统,导出了最优保代价控制器存在的充分条件。闭环系统不但渐近稳定,而且性能指标小于某一代价值。采用线性矩阵不等式(LMI)技术,给出了该控制器的设计方法和参数化表示。并将所得的控制器应用到永磁同步电动机混沌系统中,建立了永磁同步电动机混沌系统的T-S模型, 针对不包含不确定参数和包含不确定参数两种情况,均得到了满意的控制效果。
2 问题的描述
在系统局部信息或专家经验存在的条件下,不确定非线性连续系统可以采用如下i条规则的T-S模糊模型进行描述:
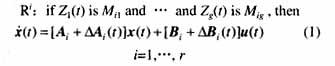
式中 Ri表示T-S模糊模型的第i条规则,也称为模糊子系统;Z1(t),…, Zg(t)为模糊规则的前件变量;Mij为模糊语言集合;x(t)∈Rn, u(t)∈Rm分别为系统的状态变量和控制变量;Ai, Bi是适当维数的实常数矩阵,DAi(t), DBi(t)是不确定矩阵,他们反映了系统模型中的时变参数不确定性。
本文考虑的不确定性假设是范数有界的且有如下结构:
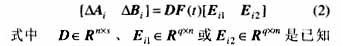
的具有适当维数的常数矩阵,它们反映了系统不确定性的结构,F(t)∈Rs×q是具有Lebesgue可测元的不确定矩阵,且满足FT(t)F(t)≤I。
上述不确定性的结构假定并不失一般性。首先,它可以表示一个含有装置和不确定性F(t)的线性关联的系统;其次,有许多系统,其不确定性可以按这种方式表示,例如,满足“匹配条件”的不确定性就可以解释成是通过输入进入到系统模型中的,即D为系统的输入矩阵;最后对一般的范数有界不确定性,总可以选择适当的结构矩阵,使其具有上面的形式。
采用文献中的单点模糊产生器,乘积推理以及加权平均模糊消除器,上述的模糊逻辑控制系统可写为如下形式中。
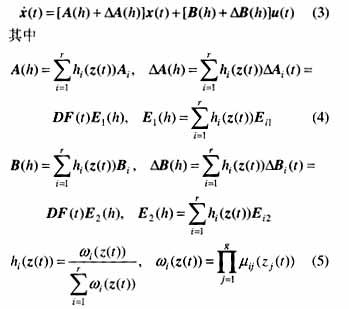


3 最优保代价控制
首先给出保代价控制的定义,然后给出模糊不确定系统(3)的稳定保代价控制器存在条件。在此基础上利用线性矩阵不等式给出控制器的设计方法。
定义1(保代价控制)考虑不确定系统(3),如果存在控制律u*(t)和正标量J*,使得对所有允许的不确定性FT(t)F(t)≤I,闭环系统是稳定的,且代价函数(9)对此闭环系统满足J≤J*,则称J*是一个保代价,而称u*(t)是不确定系统(3)的保代价控制律。
下面给出不确定系统(3)状态反馈保代价控制律存在的一个充分条件。
定理1式(7)的反馈控制律是一个保代价控制律,如果存在公共正定矩阵P∈Rn×n和矩阵k(h),使得对任意允许的不确定性F(t),有如下矩阵不等式

设存在对称阵P》0使得矩阵不等式(10)对所有允许的不确定性成立。定义Lyapunov函数为

因此,由Lyapunov稳定性理论,闭环模糊系统(11)是渐近稳定的。

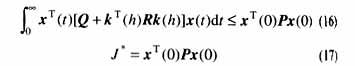
由定义1知定理1的结论成立。
下面将证明,上述推导的存在控制器使全局模糊系统渐近稳定的充分条件,可等价于线性矩阵不等式的可解性。

定理2 对于系统(11),存在对称正定矩阵P使不等式(10)成立,当且仅当存在一标量e 》0,正定对称矩阵X∈Rn×n和矩阵W(h)∈Rm×n满足如下矩阵不等式
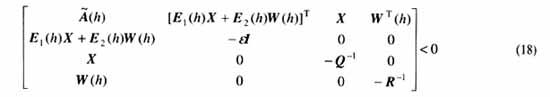

那么式(10)可被写成式(22)

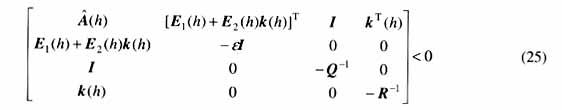
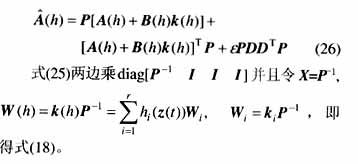
定理3 给定系统(1),存在保代价控制律(19)的条件是,存在公共正定矩阵X和矩阵Wj及标量e,满足如下线性矩阵不等式
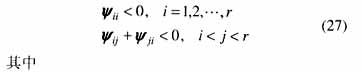
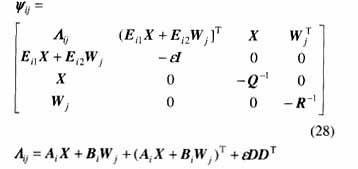
证明:由不等式(18)和式(4)可知,不等式(18)左边等于
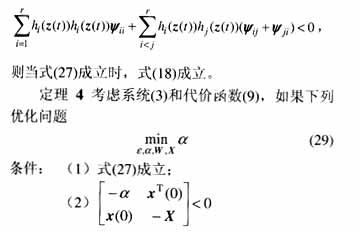
有解ε,α,W,X,则式(19)的控制律是一个无记忆状态反馈控制律,它使得不确定系统(3)的代价函数的极小值为式(20)。
证明: 根据定理2,由任意可行解ε,α,W,X所构造的控制律(19)是系统(3)的一个保代价控制律。由Schur补引理可知,式(29)中的条件(2)等价于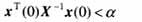
所以,由方程(20)有J*《α。
于是,极小化α隐含极小化不确定系统(3)的代价函数。而式(29)中,目标函数和约束条件的凸性,保证了该优化问题的最优性。
4 永磁同步电动机混沌系统的T-S建模与控制
4.1 T-S建模
将上述控制器应用到文献[5-6]的永磁同步电动机混沌系统。
考虑加上一个控制项的永磁同步电动机有如下形式的数学模型(其原模型见文献[5-6])
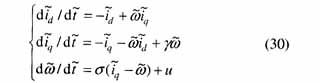
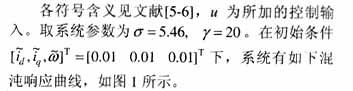
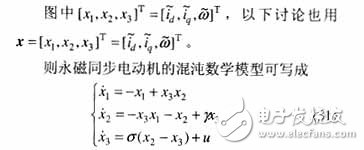
仿文献的建模过程,对永磁同步电动机建立T-S模型。将非线性项x3(t)x2(t),x3(t)x1(t)写成线性函数加权和的形式。
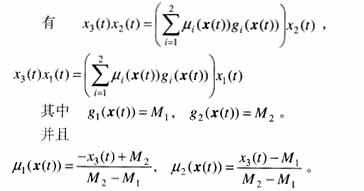
因为两非线性项都是x3的函数,则可以构造如下精确T-S模型。
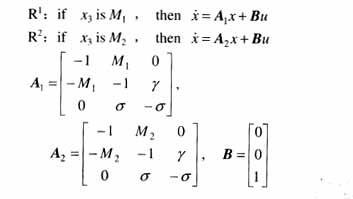
知x3(t)∈[-20,20],所以选择M1=-20,M2=20。由推导过程可看出M1,M2是一类特殊的模糊集合,即精确的数值。是一种精确建模,无建模误差。
4.2 系统不含不确定参数时的最优保代价控制
此时,DAi(t), DBi(t)都为0,故D,Ei1,Ei2也都为0。简单取e=0.1,R=1,Q=I由式(27),(29)得
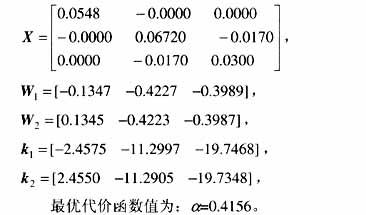
取式(7)的控制律,在初始条件为x0=(0.01 0.01 0.01)T,u=0及在t=60s加入控制项的仿真结果如图2所示,可看出加入控制项后系统趋于稳定。
4.3 系统包含不确定参数时的最优保代价控制
假设系统参数g,s 的不确定性在其标称值30%内。其不确定性代表参数摄动或建模误差。在参数30%摄动下,系统仍呈现混沌行为。仿真中每个参数加30%随机扰动,由MATLAB中的rand( )随机函数实现,则有
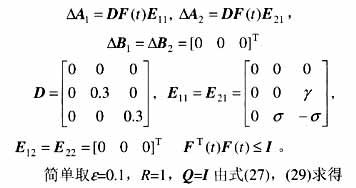
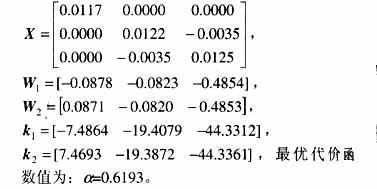
取式(7)的控制律,在初始条件为x0=(0.01 0.01 0.01)T,u=0及在t=60s加入控制项的仿真结果,可看出加入控制项后,不确定参数系统趋于稳定。
加入控制项实现了不含参数不确定性和含有参数不确定性混沌系统的稳定控制。系统状态由原来的混沌运动迅速达到平衡点。本文的控制方法与OGY法的小信号输入法不同,系统状态远离目标状态时,启动控制作用,即可将系统状态控制到目标状态,而与输入加入的时刻无关。
5 结论
基于T-S模糊模型,给出了存在稳定最优模糊保代价控制器的充分条件和相应的LMI形式。应用到永磁同步电动机混沌系统的稳定控制中,建立了永磁同步电动机混沌系统的T-S模型,对不包含不确定参数和包含不确定参数两种情况,取得了满意的控制效果。不需要改变被控系统的内部结构,具有良好的稳定性,且能达到某一性能指标最优。
-
永磁同步电动机的工作原理 永磁同步电动机的控制方法2024-02-02 2889
-
永磁同步电动机的工作原理 永磁同步电动机的优点有2024-01-19 1851
-
永磁同步电动机与直流无刷电动机有何异同2023-12-20 4690
-
永磁同步电动机如何实现自由停车?2023-11-14 1910
-
自控式同步电动机2021-08-27 1788
-
【下载】《永磁同步电动机直接转矩控制系统》胡育文 ——介绍三类PMSM直接转矩控制技术2019-12-03 4345
-
永磁同步电动机的发展趋势如何?2019-10-10 2680
-
一文阐述永磁同步电动机的综合效益2018-10-17 2428
-
基于永磁同步电动机的混沌运动控制分析2017-11-07 1155
-
基于模糊PID的永磁同步电动机数字控制系统2016-04-05 984
-
永磁同步电动机的分类和特点2014-01-22 20519
-
永磁同步电动机原理2011-12-12 4691
-
基于矢量控制的永磁同步电动机回馈制动仿真2011-08-15 1539
-
低速永磁同步电动机的设计研究2009-06-08 738
全部0条评论

快来发表一下你的评论吧 !

