

数控系统中NURBS曲线插补技术的加工方法与优势分析
描述
1. 前言
数控系统的NURBS曲线插补技术是基于PC开放式数控系统的发展关键技术之一。数控加工时经常遇到诸如飞机的机翼、汽车流线型覆盖件、成型模具型腔、汽轮机叶片等许多具有复杂外形型面的零件,CAD/CAM通常用列表曲线来描述它们。列表曲线的拟合方法很多,如三次样条、B样条、圆弧样条及牛顿插值方法等。由于NURBS曲线具有良好的直观性,且在“局部性”及收敛、逼近性方面占有优势,已经成为当前最为通用的列表曲线拟合方法,利用NURBS在CAD/CAM系统中可以使所有的曲线具有统一的数学表达式,国际标准化组织(ISO)在其正式颁布的工业产品几何定义STEP标准中,亦将NURBS作为产品交换的国际标准。于是,对CNC添加NURBS曲线曲面插补功能,成为现代开放式数控系统的关键技术之一。基于PC开放式数控系统可以充分利用PC的强大计算能力,实现NURBS曲线曲面高速度高精度的实时插补。
2.数控插补原理
在CNC系统中,插补器的硬件功能全部或部分地由计算机的系统程序来实现。CNC根据来自数据处理结果缓冲区中存储的零件程序数据段的信息,以数字方式进行计算,不断向系统提供坐标轴的位置命令,这种计算叫做插补计算,简称插补。插补软件的任务是完成在轮廓起点到终点的中间点的坐标计算。尤其对于轮廓控制系统而言,插补是最重要的计算任务。插补必须是实时的,即必须在有限的时间内完成计算任务,对各坐标轴分配速度或位置信息。插补程序的运行时间和计算精度影响着整个CNC系统的性能指标。总结目前普遍应用的插补算法可分为两类:
(1)脉冲增量插补。脉冲增量插补也称为行程标量插补,就是用软件模拟NC系统常用的逐点比较法、DDA积分法以及这两种算法的改型算法。插补的结果是产生单个的行程增量,以一个个脉冲的方式输出给步进电机。脉冲增量插补输出的频率主要受插补程序所用的时间限制,适用于中等精度和中等速度,以步进电机为驱动元件。
(2)数据采样插补。数据采样插补也称为时间分割插补,适用于闭环和半闭环以直流或交流电机为执行机构的位置采样控制系统。插补程序的调用周期可以和系统的位置采样周期相同,也可以是采样周期的整数倍。在这种系统中,插补程序的运行时间不多于计算机时间负荷的30%-40%,在其余时间内,计算机可以实现显示、译码、刀补等数控功能。本文所研究的NURBS曲线插补算法就属于这一类插补算法。
3. 参数曲线直接插补算法基础
曲线表示主要有两种方法:隐式方程法和参数方程法。参数方程法因其易于编程和计算成为CAD系统首选的曲线表示方法。一个三维曲线就可以用如下的参数方程表示:
x = x(u), y = y(u), z = z(u)
其中抽象参数u满足0 < u <1。曲线的参数方程可以非常方便的控制多轴机床的运动,而且对各轴的控制可以是分别、独立的进行,故数控系统的各种曲线直接插补算法都基于曲线的参数方程。通常把这三个方程合写成p(u) = [x(u), y(u), z(u)],或者笛卡儿分量表示形式P(u) = x(u)i + y(u) j + z(u)k ,其中i, j, k 分别为沿x, y, z轴正向的三个单位矢量。常简记Pi = p(ui)。
插补计算就是在CNC系统的第i-1工作周期中,实时计算出满足指定加工要求的下一个工作周期的各轴运动分量ΔPi 。例如满足加工步长要求ΔLi的插补点Pi + 1为:

3.1 B样条曲线的定义
非均匀有理B样条曲线NURBS方法提出的首要理由是,为了找到与描述自由型曲线的B样条方法相统一的、且又能精确表示二次曲线弧与二次的数学方法。因此在了解NURBS曲线之前,有必要首先了解B样条曲线,B样条曲线是采用控制顶点来定义曲线的,其曲线方程可写为:

Ni, k(u),i = 0,1,K , n称为k次规范B样条基函数,其中的每一个k次规范B样条基函数简称为B样条。它是由一个称为节点矢量的非递减的参数u的序列U: u0 ≤ u1 ≤K ≤ ui + k + 1 所决定的k次分段多项式.
B样条基Ni, k(u)通常采用截尾幕函数的差商定义,德布尔一考克斯的递推定义为:
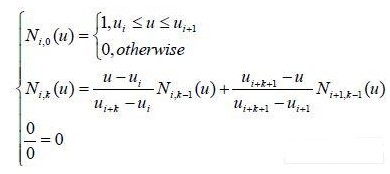
Ni, k(u)的双下标中第二下标k表示次数,第一下标i表示序号。该递归公式表明,欲确定第i个k次B样条Ni, k(u),需要用到ui,ui + 1,K ui + k + 1共k+2个节点,包含的区间[ui,ui + k + 1]被称为Ni, k(u)的支承区间。Ni, k(u)的第一下标等于其支承区间左端节点的下标,即表示该B样条在参数u轴上的位置。曲线方程(23)中相应的n +1个控制顶点di,i = 0,1K n,要用到n +1个k次B样条基函数Ni, k(u),i = 0,1,K , n。它们的支承区间的并集,被定义为这一组B样条基的节点矢量U = [u0,u1,K un + k + 1]。
3.2 NURBS曲线的定义
在B样条曲线定义的基础上,若节点序列为非均匀分布,且在每个控制点处加一个表示对曲线形状影响大小的加权因子Wi,则k阶B样条曲线相应的变为k阶NURBS曲线,其公式相应为:
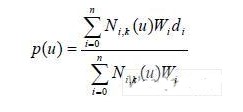
对于非周期NURBS曲线,往往取u0 = u1 =K = uk = 0,un + 1 = un + 2 =K = un + k + 1 =1,即将两端节点的重复度取为k+1,从而使曲线两端能相切通过控制多边形的首、末端节点。于是,曲线定义域u∈[uk,un + 1] = [0,1],节点矢量U = [0,0,K 0,uk + 1,K ,un,1,1,K 1]。而且由于NURBS曲线方程的有理性,使得寻求NURBS曲线的迭代公式变得相当困难。
4.NURBS曲线插补技术
4.1 传统的CNC机床的加工方法
图1描述了CNC机床传统的曲线加工方法。首先,用CAD系统软件设计加工零件的几何模型,然后由CAM系统将刀具接触轨迹转化为刀具位置轨迹。以为目前的CNC系统一般只具有直线和圆弧插补功能,为了确保CNC系统能控制机床沿着刀具位置轨迹来执行加工任务,刀具位置轨迹通常被分解为一系列直线段或圆弧段(也称为NC代码)。应用足够数量的直线段或圆弧段,就可以在指定的精度内逼近给定的曲线。但这种方法存在以下缺点:
1) 由于用直线逼近曲线本身是用直线代替曲线,逼近后的线是一阶的,导矢不连续的,所以加工表面不光滑。
2) 在曲线的加工过程中,如果在直线部分不进行加减速,那么就要求在较低的速度下进行加工,这样一来不能满足高速加工的要求。并且由于直线段的一阶不连续,在加工过程中会造成机床的过冲,不能保证加工的质量和精度要求。如果在曲线的加工过程中,对直线段部分的每一段直线进行加减速,会造成加工速度的不平衡,加工的质量差,时间长。
3) 大量的直线段或圆弧段将会增加加工速度的变化和曲线的加工时间,这样将会降低曲线的平均加工速率,降低加工效率。
4) 具有复杂曲面形状的零件的加工,需要存储的程序段数非常庞大,而CNC系统的内存容量相对较小,因此需要分段存储和调用,这不仅会降低系统的可靠性,也会降低加工效率。
通过设定曲线加工时的允许误差和曲线曲率或者待加工曲线的长度,就可以确定加工任务中的最小直线段数。如果刀具实际走过的直线或圆弧段数太少,将会引起实际加工的曲线的一阶和二阶导矢的不连续。进而导致加工后的工件表面的光滑性和曲面的光洁度的畸变。基于以上分析,如果采用传统的直线和圆弧的插补器,很难获得高速,高精度的曲线加工。所以,开发一种新型的CNC插补器是十分必要的。
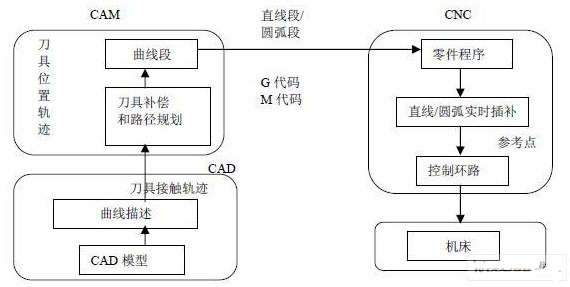
图1 CNC机床传统的曲线加工方法
4.2 采用NURBS插补技术的CNC机床的加工方法
图2描述了一种新型的CNC机床的曲线曲面加工方法。在这种加工模式下,数控机床在它的伺服控制环中配备了NURBS曲线的实时插补器。因为NURBS曲线的定义参数较少,并且即可以表示解析曲线,又可以表示自由曲线,所以可以节省大量的花费在CAD/CAM和CNC机床之间的数据传递时间。
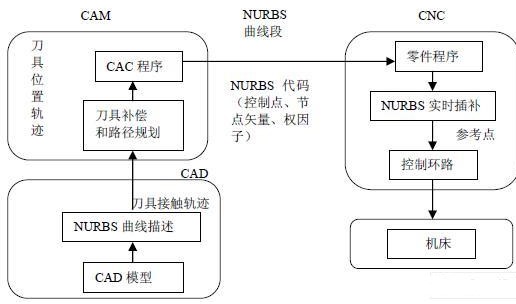
图2 采用NURBS插补技术的CNC机床曲线曲面加工方法
一个三轴联动的数控机床的伺服控制结构图如图3,其中CNC运动控制器的主要任务可以分为三部分。第一部分就是解释从CAD/CAM系统中获得的加工代码。第二部分是将从第一部分中获得的数据在一个采样周期中转变为CNC的伺服控制命令。第三部分就是在CNC控制器的各个运动轴上执行伺服控制命令。因为运动控制必须实时地进行,所以这三部分任务必须在一个给定的采样周期内完成。因为代码解释通常都是在数控加工开始之前就完成了,所以第一部分任务不必实时完成。而且采用NURBS的加工方法只占用少量的程序内存,花费在曲线解释上的时间可以大大的减少,因而总的加工时间也得以减少。因此在图3中只有第二部分和第三部分需要实时进行。随着伺服控制技术的发展,第三部分已经能够实时的实现,所以,为了能够成功地实现数控加工的实时运动控制,第二部分的命令生成任务必须在一个采样周期内完成。
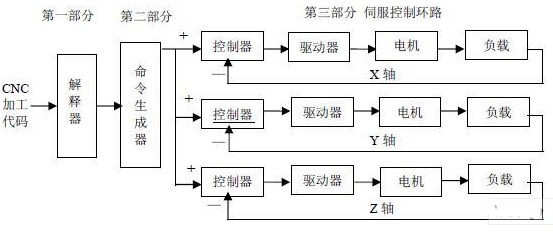
图3 三轴联动数控机床的伺服控制结构图
5.结语
在现代开放式数控系统中,引入NURBS曲线进行插补,能有效地提高实时插补的速度和精度,从而进一步提高数控系统的工作效率。
-
数控系统分类及其优缺点有哪些2024-07-01 3670
-
数控系统刀尖半径补偿方法2022-07-11 17179
-
CK210sp迷你小型数控车床2021-09-02 1583
-
新型NURBS曲线插补算法2018-03-27 816
-
数控系统参数曲线、曲面插补算法及加减速控制研究2016-05-03 576
-
基于DSP的NURBS曲线插补控制2010-08-05 451
-
数控系统中的NURBS曲线插补技术2009-07-30 1209
-
基于四次位移曲线的CNC数控系统的研究2009-05-17 3991
全部0条评论

快来发表一下你的评论吧 !

