基于TMS320F206 DSP芯片的冗余度TT—VGT机器人运动学设计方案

近年来自动控制技术发展迅猛，特别是计算机技术、网络和通信技术发展的突飞猛进，使人们籍助于许多使能技术的进步和一些开发工具的扩大，将人们构思的自动操作得以付诸实现。如网络控制技术、可编程控制器等均属于自动化控制技术中的使能技术。自动控制技术正向着网络化、集成化、分布化、节点节能化的方向发展。数字信号处理器（DSP）在自动控制中得到了越来越广泛的应用。这主要是因为它具有以下优点：（1）并行体系结构和专用的硬件乘法器使得DSP运算能力极强；（2）高速特性使得DSP能实现实时处理和实时控制。

据调查，目前将DSP应用于机器人控制系统的方案，通常是将机器人位置控制中运动学计算任务交给PC机完成，PC机将计算结果（机器人各关节的转角）下载到以DSP芯片为核心的电机控制器，实现机器人控制眼演。本文提出将机器人运动学计算任务直接交给DSP的控制方案，利用DSP 的并行性计算特点，提高了计算速度，缩小了控制系统的体积。仿真结果表明，该方案计算精度和实时性都较好。

1 TMS320F206 DSP结构特点

TMS320F206是TI公司推出的一种DSP芯片，它是基于TMS320C5x之上的高速定点数字处理芯片，具有改进的哈佛结构并行分离的程序和数据总线、高性能CPU及高效的指令集等特点。其主要特性如下：

CPU具有32位CALU、32位累加器、16×16位并行乘法器、三个移位寄存器、八个16位辅助寄存器。

存储器具有224K字可寻址存储空间、544字片内DRAM、4K字片内SRAM或32K字片内快闪存储器。

指令速度为50ns、35ns及25ns单指令周期。

外围电路有软件可编程定时器、软件可编程等待状态发生器、片内锁相环时钟发生器、同步和异步系列串口。

2 TT-VGT机器人的位姿逆解

TT-VGT（Tetrahedron-Tetrahedron-Variable Geometry Truss）机器人是由多个四面体组成的变几何桁架机器人，图1所示为由N个四面体单元组成的冗余度TT-VGT机器人操作手，平面ABC为机器人的基础平台，基本单元中各杆之间由较铰连接，通过可伸缩构件li（i=1,2,…，n）的长度变化改变机构的构形。图2所示为其中的两个单元的TT-VGT机构，设平面ABC和平面BCD的夹角用中间变量qi（i=1,2,…，n）表示，qi与li（I=1,2,…，n）的关系。

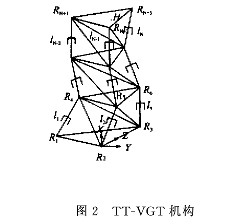
设冗余度TT-VGT机器人操作手由N个伸缩关节组成,图3所示为两个单元的TT-VGT机构。设变量qi(i=1，2…N)为平面ABC和平面BCD的夹角,其相应的速度和加速度分别为 

相邻两个四面体单元的坐标系的建立如图3所示。坐标系XiYiZi相对于坐标系Xi-1Yi-1Zi-1的变换矩阵可表示为:

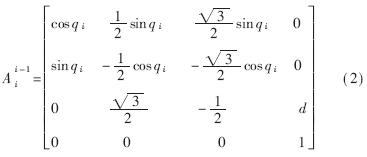
对于机构自由度为N、任务自由度为L的冗余度TT-VGT机器人,其余四面体单元的结构与坐标系的建立与图3所示的相似。由文献[1]可知,其末端位姿X是中间变量qi(i=1,2,…,N)的函数,有:

对式(3)求导,可得如下的运动学方程式:

将式(6)离散化,可得机器人运动轨迹上第k点各关节中间变量的dqk及位置qk:

将qk代入式（1），可求得TT-VGT机器人各伸缩构件的长度li.

3 TMS320F206 DSP运动学程序设计

对于TT-VGT机器人的位姿逆解，采用DSP汇编语言设计的程序流程进行求解，如图4所示。

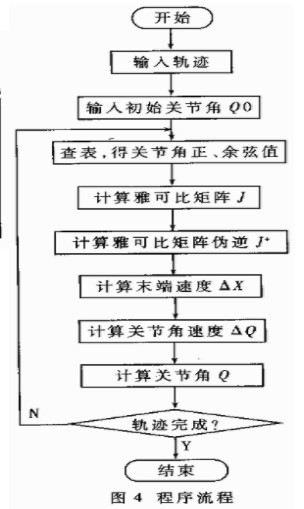
为了保证该程序的执行速度和计算精度，采取了以下算法：

（1）由于汇编语言指令系统中没有三角函数等数学函数指令，这些函数的计算只有通过级数展开算法实现，但计算量太大。考虑到三角函数的周期性，建立了一个1024点的正弦函数和余弦函数表，其分辨率完全能满足精度要求。

（2）由于TMS320F206 DSP芯片为定点运算器件，因此需要将浮点运算转换为定点运算。为了保证计算精度，将数据定标设定为可动态调节，数据表达能力为从Q13（-4~+3.9998779）到Q0（-32768~+32767）。

（3）采用并行指令，充分利用TMS320F206四级流水线操作，来提高程序运行速度。

如：

MAC                       ;乘并累加

APAC                      ;累加

SACH*+,3,AR2              ;将计算结果左移3位后，存于当前辅助寄存器（AR）所指的存储器单元中，并将

AR内容加1,最后，将AR2设定为当前AR.

（4）对运算过程进行优化，既要减少计算量，又要防止计算溢出；在混合运算中采用"先除后加"、"加减交叉"的方法。

（5）尽量采用移位运算代替乘除运算，以提高运行速度和计算精度。

通过以上方法，实现了机器人运动学计算的实时性和准确性。

4 仿真计算

以四重四面体为例，建立如图5所示的基础坐标系XYZ,末端参考点H位于末端平台EFG的中点。设参考点H在基础坐标系中从点（0.522689,-0.818450, 0.472752）直线运动到点（0.771439,-0.965700,0.721502），只实现空间的位置运动，不实现姿态。运动的整个时间T设为5秒，运动轨迹分为等时间间隔的100个区间。设各定长构件长度为1m.

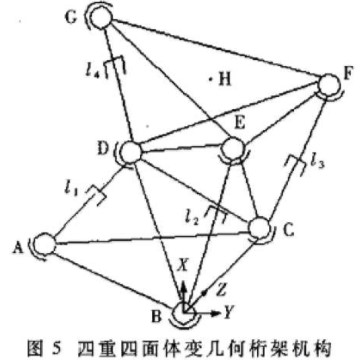
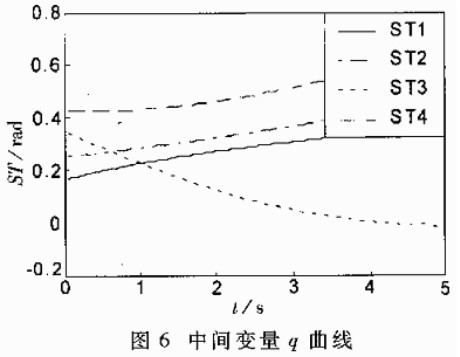
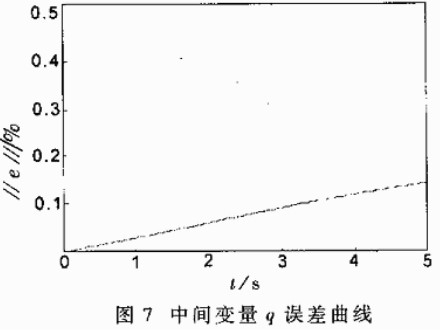
中间变量q曲线和中间变量q误差曲线如图6和图7所示。从误差曲线可看出,采用TMS329F206 DSP芯片进行的运动学计算精度较高。经过实测,该计算程序运行时间为34ms(TMS320F206芯片指令周期为25ns),可见其实时性较强。

本文提出的采用TMS320F206 DSP芯片进行冗余度TT-VGT机器人运动学计算方案，充分利用了DSP 并行特性进行机器人位姿逆解计算，在程序设计中采用了多种技巧优化计算。仿真结果表明，该方案计算误差较小，实时性强。因此，可将其应用于机器人控制系统，实现机器人计算和控制任务一体化，从而大大缩小机器人体积、降低成本、增强灵活性、具有较强的先进性和实用性。