

SCARA机器人处于直线运动状态的算法求解研究
描述
1. 引 言
SCARA机器人是一种四轴机械手,SCARA(Selective Compliance Assembly Robot Arm,中文译名:选择顺应性装配机器手臂)是一种圆柱坐标型的特殊类型的工业机器人。 SCARA系统在x,y方向上具有顺从性,而在Z轴方向具有良好的刚度,此特性特别适合于装配工作,例如将一个圆头针插入一个圆孔,故SCARA系统首先大量用于装配印刷电路板和电子零部件;SCARA的另一个特点是其串接的两杆结构,类似人的手臂,可以伸进有限空间中作业然后收回,适合于搬动和取放物件,如集成电路板等。 它的第一、二、四轴具有转动特性,而第三轴具有线性移动特性,故其工作空间类似于一个扇形柱体区域。SCARA机器人还广泛应用于塑料工业、汽车工业、电子产品工业、药品工业和食品工业等领域
SCARA机器人是专门为工业要求而开发的机器人系统,适合在平面范围内实现对物体的快速取放或者装配等。控制系统硬件平台采用四轴运动控制器与交流伺服驱动系统,结构紧凑,可靠性高 谐波减速传动 控制系统软件平台采用OpenRob-I工业机器人平台软件,机器人语言编程系统全面开放,提供源代码,方便应用软件的二次开发,用户可根据需要进行机器人专用系统的开发 工业标准设计,可同时兼顾教学和实训当SCARA机器人在流水线上进行往复运动时,其末端点经常会处于直线运动状态。由于末端位置与工作空间会随实际工况的要求而发生变化,预先确定末端在直线运动下的极限点坐标,并提前设定软件限位,对于防止过度驱动或错误操作下的机器人碰撞与损坏。
2. 算法设计
假定SCARA机器人的基座安装在水平面内,依照从基座到末端的顺序,将其四个轴分别命名为X、Y、Z、R轴,且将R轴末端视为一个点(设为End),若在R轴末端安装夹具,则将夹具末端也视为一个点(设为Tip)。
2.1 前提条件
本算法的实现基于如下三个客观前提条件:
(1) 由于Z轴仅在竖直平面内做上下运动,并不会影响End点的水平面投影位置。而在不安装夹具的情况下,R轴的旋转运动也不会对此产生影响;再者,由于夹具没有附带对应的驱动装置,即使安装夹具也仅相当于将End点的水平面投影点在二维空间内相对平移了一个固定的矢量位置,扩展了一定的工作空间范围,所以,Z轴和R轴的运动都不会影响到末端点的水平面投影位置。
(2) 由于SCARA机器人的工作空间是一个类似于扇形的柱体区域,将其投影在水平面上并不会使工作空间的边界发生改变。所以,End点的直线运动是否超出工作空间的范围仅与X、Y两轴的运动有关。
(3) 由于End点(或Tip点)在水平面二维空间下的直线运动有无穷多种可能的方向,而每种方向均与x-y直角坐标轴成一定角度,经旋转变换后都能归结到与坐标轴平行的方向上。所以,本算法只针对分别平行于x-y直角坐标轴的两种直线运动求解四个极限点坐标即可,其余运动方向上的极限点坐标可参照本算法旋转相应角度后求解。
2.2 设计过程
设基座位于x-y直角坐标系的原点O,SCARA机器人的大、小臂均完全展开时的姿态与x轴正向重合,为初始状态,规定两臂旋转的方向均取逆时针为正,顺时针为负,据此建立几何学模型。先由四条平面圆弧(设为C1~C4)确定水平面工作空间,同时给定末端当前点(设为Now)的坐标;再过点Now分别作两条坐标轴的平行线(设平行于x轴的直线为Line_H、平行于y轴的直线为Line_V),与边界圆弧相交;然后分别求出Line_H、Line_V与C1~C4的8个交点,若无交点则默认交点坐标为点Now的坐标值;接着判断交点中的有效点;最后确定出四个极限点(设为P1~P4)的位置坐标即为所求。
2.3 交点判定
从上述设计过程可知,所求的左、右极限点必然在Line_H与圆弧边界的交点之中,而上、下极限点必然在Line_V与圆弧边界的交点之中。点a称为集合E的极限点,如果a的任意邻域都与E有交集。因为SCARA机器人在做直线运动时不会更换手系,所以可将左、右手系分开考虑。
在右手系下,圆弧C1~C4依次首尾相连围成一个封闭区域,如图1所示。其中,C1弧为小臂处于正向最大姿态且大臂自由运动时End点的轨迹,C2弧为小臂始终处于大臂的延长线上且大臂自由运动时End点的轨迹,C3弧为大臂处于正向最大姿态且小臂自由运动时End点的轨迹,C4弧为大臂处于负向最小姿态且小臂自由运动时End点的轨迹。Now点位于这个封闭区域内,P1~P4点的判定遵循如下原则:(1) P1、P2、P3、P4分别位于Now点的左、右、下、上方;(2) 各极限点在各自方位上均与Now点的直线距离最短;(3) 线段P1P2、P3P4均不穿过C1弧与坐标原点O围成的工作死区。
左手系与右手系类似,不再敖述。
3. 仿真与实现
本文采用MATLAB仿真与VC实现相对应验证的方式对算法加以说明。MATLAB是矩阵实验室(Matrix Laboratory)的简称,是美国MathWorks公司出品的商业数学软件,用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境,主要包括MATLAB和Simulink两大部分。MATLAB是由美国mathworks公司发布的主要面对科学计算、可视化以及交互式程序设计的高科技计算环境。它将数值分析、矩阵计算、科学数据可视化以及非线性动态系统的建模和仿真等诸多强大功能集成在一个易于使用的视窗环境中,为科学研究、工程设计以及必须进行有效数值计算的众多科学领域提供了一种全面的解决方案,并在很大程度上摆脱了传统非交互式程序设计语言(如C、Fortran)的编辑模式,代表了当今国际科学计算软件的先进水平。
3.1 MATLAB仿真
3.1.1 右手系

设最大工作空间取值范围如下:X轴为 ,Y轴为 ,当前末端点位置坐标为 ,最终所求的右手系下的4个极限点P1、P2、P3、P4的直角坐标值为(如图2所示):
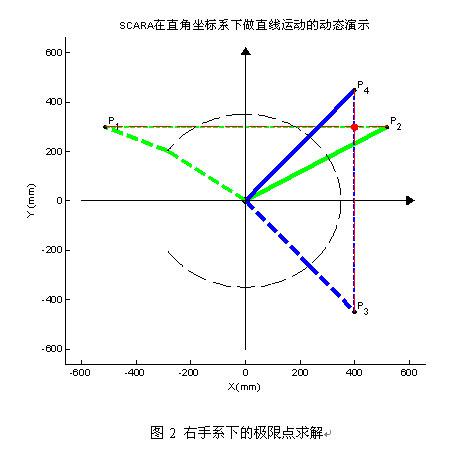
3.1.2 左手系
左手系下的实现过程与右手系类似,如图3、图4所示。不同的只是Y轴的工作空间取值范围为 ,当前末端点位置坐标仍然取为 ,最终所求的左手系下的4个极限点P1、P2、P3、P4的直角坐标值为(如图4所示):
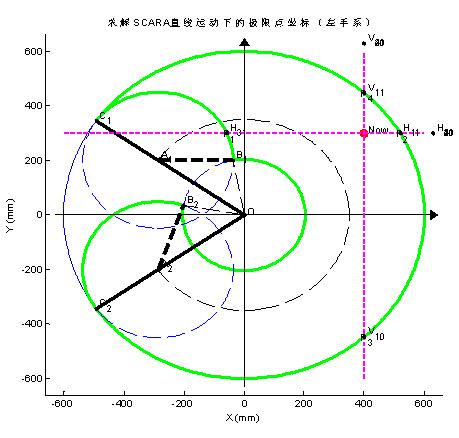
图3 左手系下的工作空间与当前点
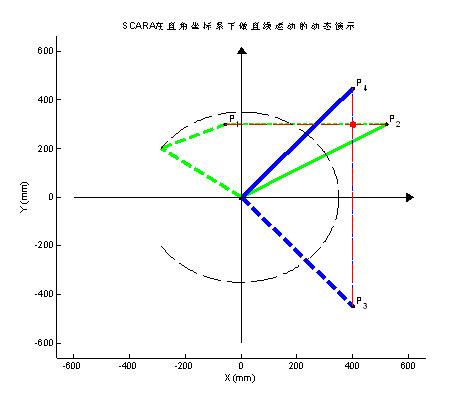
图4 左手系下的极限点求解
需要说明的是,上述仿真示例只是给出了最大工作空间,在该工作空间内可选取任意子空间及包含其中的当前末端点进行仿真,仿真结果均表明,本算法能正确计算并确定SCARA机器人末端直线运动下的四个极限点坐标。
3.2 VC实现
采用VC开发软件封装功能函数,实现本算法。右、左手系下的界面分别如图5、图6所示。选取与上节MATLAB仿真示例中相同的工作空间与末端当前位置坐标等参数,求解出的四个极限点坐标与MATLAB结果完全对应相同。
3.2.1 右手系

3.2.2 左手系

图6 左手系下的算法实现
4. 结 论
本文提出了一种SCARA机器人直线运动极限点的求解算法,并通过MATLAB仿真与VC实现进行了对应验证。该算法能有效预测并解决实际操作中的安全问题,具有较强的实用价值。SCARA机器人)是应用最广泛的一种装配机器人。本文设计的SCARA机器人既可以用于实际生产又可以用于教学实验和科学研究。所以开发SCARA机器人具有广泛的实际意义和应用前景。
-
abb工业机器人的运动模式有哪些2024-06-17 5471
-
ABB工业机器人运动指令有哪几个2024-06-16 4919
-
LabVIEW的六轴工业机器人运动控制系统2023-12-21 3855
-
直线电机是如何做到直线运动的呢?2023-10-07 3034
-
全向轮机器人是如何进行直线运动的?2021-10-29 1866
-
全向轮机器人是怎样进行直线运动的?2021-08-30 1040
-
SCARA工业机器人相关资料推荐2021-07-01 1356
-
scara机器人运动学反解,各位大佬求救吖2021-06-29 39891
-
基于CAN总线和双传感器仿人机器人运动控制系统的研究2020-08-19 2582
-
单轴与多轴机器人的优缺点PK(深度总结)2017-11-23 3565
-
S4C IRB机器人基本操作2017-10-16 781
-
先进机器人控制2017-09-19 4390
-
大族机器人-SCARA2016-12-25 694
-
移动机器人运动控制系统设计及控制算法研究2012-08-20 3395
全部0条评论

快来发表一下你的评论吧 !

