浅析计算机中物理内存的模型

小伙伴们有没有好奇，数据在计算机内存中，是如何存储的？计算机中物理内存的模型是怎样的呢？今天大雄就给大家详细的介绍一下。

在了解存储模型之前，我们首先应该了解一下计算机的存储体系。

个人感觉学这部分的知识应该首先在脑海中抽象出存储体系，因为无论磁盘，物理内存还是虚拟内存都是互相有联系的，抽象出模型有助于我们的理解和记忆。接着需要哪部分知识或再次深入哪部分知识，从体系图中找。

建议不要在这块知识拉长战线，看了前面忘后面。

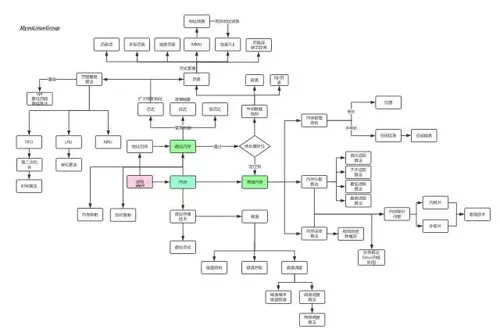
计算机存储体系图

简述上图：

从进程开始，我们知道进程运行在内存中，每个进程都有自己独立的内存地址空间，目的是安全和高效利用内存，一个进程的地址空间是抽象出来的，属于虚拟内存，而内存分为虚拟内存和物理内存。

从物理内存分析，物理内存管理分为等长和不等长划分，等长划分一般通过位图来记录结构，不等长划分一般通过空闲区表来记录。

而物理内存的要通过算法来使进程合理分配回收，其中分配算法有四种，回收算法分为四种情况，而内存分配和回收会引起内存碎片问题，内存碎片问题分为内碎片和外碎片，解决方案有压缩技术。

从虚拟内存分析，分为页式/段式/段页式内存管理，中间通过页表/段表/段页表来进行物理到虚拟内存的转换，重点是页式管理，页式管理中重要的概念有页表项，多级页表，倒排页表，MMU，快表TLB和页错误/缺页异常，而虚拟存储技术中核心概念就是将内存中暂时不用的页面（内存块）放入磁盘上，问题是哪些页面（内存块）放到磁盘上呢，于是我们引入页面置换算法，其中OPT为理想置换算法，基本算法有FIFO，FIFO改进后的第二次机会算法和时钟算法，LRU中老化算法和NRU，既然部分页面暂存到磁盘上，那么就要聊聊磁盘。

磁盘是硬件，所以要讨论它的结构，和如何存取数据，以及磁盘调度的一些算法，此外，虚拟内存还有重要的两个技术就是内存映射和写时复制。

物理内存

物理内存其实就是我们机器的实际内存大小，比如我的笔记本电脑内存是4G。我们都知道程序是要加载道内存中才能执行，所以物理内存越大，我们电脑的性能就越好。

位图

位图(bitmap)，其实就是用位来标记数据。

在等长内存管理中，比如我们将内存等分为大小相同的内存块，那么一位标记一块，因为会形成一个位图。

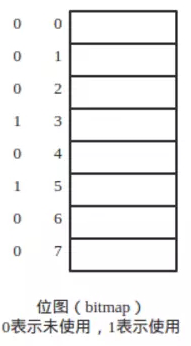
这样，我们需要多大的块，只需要匹配bitmap中连续多少个0即可。

空闲区表

在不等长划分中，比如我们根据进程的大小来分配内存，这是就需要采用空闲区表来存储空闲的内存。

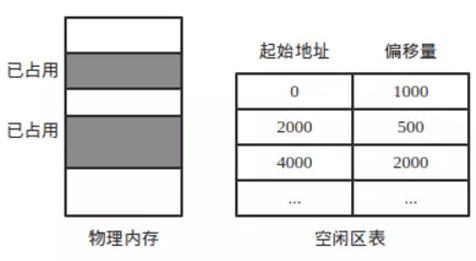
空闲区链表只不过是通过链式结构将空闲区表中的数据组织起来。

内存分配算法

上面说了我们如何通过数据结构来组织未分配的内存，我们以空闲区链表结构为例，下面来说说物理内存的分配算法，有如下四种。

1.首次适配算法

首次适配算法是在空闲区链表中从头开始查找符合申请内存大小的块，直到找到满足条件的为止，该算法不断的从头开始试验申请，所以大部分使用的都是低地址空间的内容，从而流出了高地址空间来满足大的申请需求，但是缺点是会在较低的地址空间中频繁的申请和释放导致低地址空间中的内存碎片，而且每次都查找都从头开始，查找效率比较低。

2.下次适配算法

下次适配算法是首次适配算法的一个改进，它每次从上一次适配的地方开始向下查找，不需要每次都从头开始，此算法使得内存使用均匀，但是不会有大的内存块来满足内存分配。

3.最佳适配算法

此算法先按照内存块的空闲区大小从小到大进行排序，排序后，每次从头开始匹配，这样匹配出来的结果肯定是最优的，但实际因为比较符合申请内存的大小，会出现很多较小的内存碎片无法使用，并且每次分配后都要重新排序，开销比较大。

4.最差适配算法

此算法按照内存块的空闲区从大到小进程排序，排序后，有进程申请内存时，将表头最大的内存块分配给它，这样如果不能分配则所有不能分配，且将大内存分配给它，若只占用一小部分还可以进行二次分配。

内存回收算法

内存分配且进程使用完后，我们要进行回收，一般而言，内存回收算法和内存的分配算法有着密切的关系。

所以我们仅仅看内存回收算法可能会出现的四种情况。

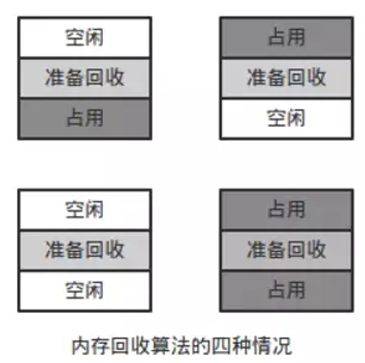
左上为上相邻，右下相邻，左下是上下相邻，右下是上下不相邻。

内存碎片

什么是内存碎片，就是在内存中占据一定大小的空间却得不到利用的内存。内存碎片分为内碎片和外碎片。

内碎片：比如按页式分配等长，那么如果有一个进程需要5页多内存，那么我们只能给他分配6页内存，那么这第6页是未用完的，其中除过一些数据外，我们还有空闲的被该进程占据，其他进程也不能使用。

外碎片：外碎片是还未分出来的，未被进程占用且因为太小或其他不满足条件再次分配的小的内存块称为外碎片。

紧缩技术：我们一般采用紧缩技术来合并小的内存碎片，原理是将暂时不运行的进程安全的移动位置，独立出内存碎片，从而组装多个内存碎片合并成一个大的内存块。

注意的是有些进程并不能被移动，比如正在读写IO。

伙伴算法

伙伴算法是Linux底层内存分配回收算法的一种实现。本文只讲述伙伴算法的基本原理。

伙伴算法基本思想：

将内存大小变为二的n此方 。

如果一个程序申请的内存块大小 m 满足 2^n-1 < m < 2^n条件，那么就将此时的内存块分配给它。

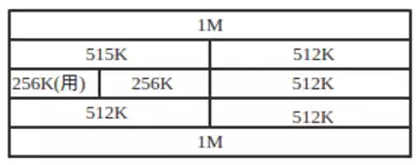
如上图，我们现在需要200K空间，1M等于1024K，如果m小于1M的一半，那么继续分离m，当分离到256时，刚好能满足200K的需求，所以分配。

归还时，采用内存回收算法的思想，看左右相邻。若没被占用则合并（也是为什么叫伙伴算法）。