基于相位增量的相位优化快速算法分析

1引言

正交频分复用是一种多载波调制技术，具有很高的频谱利用率，能够有效减小无线信道的时间弥散所带来的ISI。广泛应用于现在流行的高速无线通信技术中，如WIMAX和WIFI。OFDM技术有2个关键问题：对频率偏差敏感，峰均功率比值较大。这是因为OFDM信号在时域上表现为N个正交子载波信号的叠加，理论上峰值功率可以达到均值功率的N倍。尽管峰值功率出现的几率很低，但为了不失真地传输这些信号，对发射端的线性度要求很高，并且过大的功率会造成很大浪费，系统的性能也会急剧恶化，他直接影响整个系统的运行成本和效率。因此必须寻找降低峰值平均功率比的方法。

目前已经提出很多方法来解决PAPR的问题，包括限幅类技术、编码类技术、概率类技术。其中概率类技术中部分传输序列(PTS)算法是一种解决高PAPR问题的有效方法，他通过对符号作线性划分和线性变换，可以显著减少信号峰值出现的概率。

2峰均功率比的定义

OFDM系统中的峰均功率比是指OFDM信号的最大峰值功率和其平均功率之比，即：

式(1)中xn表示经过反傅里叶变换后得到的一个OFDM符号；E[]代表数学期望。N点M进制的输入序列[x0，…，xn-1]，将星座映射后的数据序列分别调制在N个子载波上，在一个OFDM符号周期内，基带OFDM符号可以等效表示为：

对连续时域信号s(t)以T／N的速率进行抽样，即令t=kT／N(k=0，1，…，N-1)，可以得到离散的时域信号s(k)：

从式(5)上可以看出，降低PAPR技术的核心就是降低R(u)，也即是降低传输信号序列的相关性。当输入数据序列的一致性较大时，OFDM峰均功率就比较高。假定当输入二进制数据序列为全1序列，那么经过星座映射和IFFT调制后，信号会产生很大的瞬间峰值功率，从而导致PAPR达到理论上的最大值N。

3部分传输序列(PTS)方法原理

PTS方法的基本原理如图1所示，其中，输入的数据符号被分为若干组，然后再合并这些分组，通过选择适当的分割方法和适当地改变相位以选择最优的序列，从而实现提高系统性能和降低系统的复杂度。

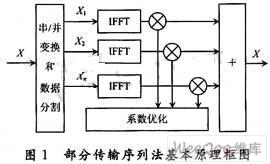
4一种基于相位调整的PTS搜索算法

PTS算法的关键是计算最优的旋转向量b=6[bn(1)，…，bn(v)]，通常采用穷尽搜索的方法。需要做Wv-1次循环比较。特别是当V较大时，计算的复杂度将呈指数上升。对于比较大的子载波数目(V>8)，计算的负担使得全局搜索难以实现。已经有一些方法减少系数搜索的复杂度。一些文献提出一种迭代方法，减少了搜索次数得到相位因子的一个次最优集合，就是将输人的数据块分成V束，IFFT变换之后得到V个N点的部分序列。首先假定所有部分序列的因子都相同b(v)=1，并计算合成信号的峰均比然后改变第一个因子b(1)的符号，重新计算新合成信号的峰均比。如果新的峰均比比上一步的低，则保留b(1)作为最终因子序列的部分，否则将b(1)变回前面的值。以相同的方式继续这个过程，直到所有V个因子都经历了符号翻转的尝试。和全局搜索比较，迭代方法有一点性能损失。也有一些文献提出了一些新的算法，把相位固定的几个特殊值上，比如说1，j，这样可将搜索降低到。然而当v很大时，这种算法的计算量还是很大。下面介绍一种基于相位调整的简单算法。基本的思想是用相位的增量寻找PAPR的最小值，相位可用以下公式表示：

可以很明显地看出，当k较大时，搜索的精度比较高，然而计算量也会同时增大。经过k次循环后，对应的较小的PAPR值才能得到。还可以设一个门限值来减少计算复杂度，当小于门限值时，相位调整中止，否则一直到循环结束。为了验证OFDM系统基于相位调整算法降低PAPR的有效性，考虑3种情况下的CCDF特性。在仿真中，采用128个子载波、QPSK调制的OFDM系统，PTS算法中用的V=4个子频域向量。算法使用的过采样倍数L=4。图2分别给出在不同相位优化算法下的PAPR改善性能。显而易见，基于相位调整的PTS搜索算法比穷尽搜索相当大程度上减小计算复杂度，而其性能却与穷尽搜索差不多。

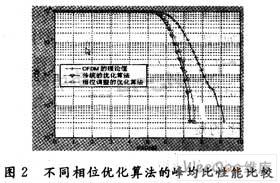
5结语

通过对基于相位优化的PTS算法研究，指出以前相位优化算法中存在大量计算，提出一种基于相位增量的相位优化快速算法。分析和仿真结果表明，新算法不但能够较大程度地减小运算复杂度，而且获得了较好的峰均比，而且特别适用于过采样处理，有利于工程实现。